巧用函数不等式lnx≤x-1简证一类数列不等式
武增明
(云南省玉溪第一中学 653100)
一、函数不等式lnx≤x-1的背景
1.切线背景
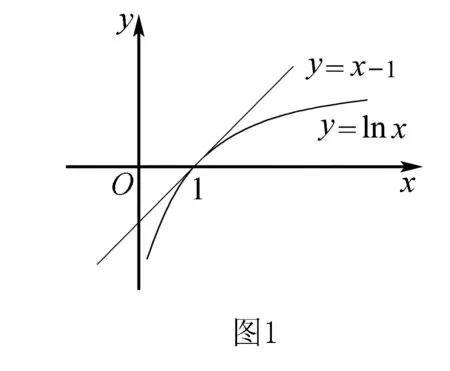
不难证明,函数y=lnx在x=1处的切线方程为y=x-1,如图1所示.观察图象可知,函数y=lnx的图象总是在切线y=x-1的下方,所以从图1中可以抽象出不等式lnx≤x-1,当且仅当x=1时等号成立.
2.函数背景
构造函数f(x)=lnx-x+1,通过求导,可证明f(x)≤0,即lnx≤x-1(x∈R+).
二、函数不等式lnx≤x-1(x∈R+)的变形
函数不等式lnx≤x-1(x∈R+)很容易衍生出十分丰富、十分优美、十分漂亮、十分简洁的不等式,这些不等式在高考函数不等式和数列不等式证明中有着十分广泛的运用.同时,每一个不等式都有很强大的放缩功能.
为了便于理解,下面以思维导图的形式给出函数不等式lnx≤x-1(x∈R+)的变形不等式.
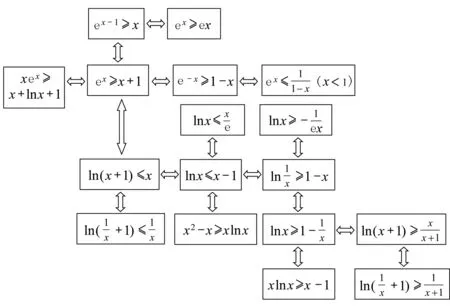
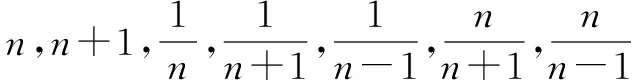
请同学们根据图1记忆函数不等式lnx≤x-1,其变形不等式要理解来龙去脉,不要孤立地刻意记忆,特别要会根据解题需要,对函数不等式lnx≤x-1及其变形不等式进行灵活赋值.
三、函数不等式lnx≤x-1(x∈R+)及其变形的运用
函数不等式lnx≤x-1(x∈R+)的赋值功能非常强大,如果对函数不等式lnx≤x-1(x∈R+)及其各种变形中的x进行不同的赋值,可使许多看似棘手的数列不等式问题得到解决.
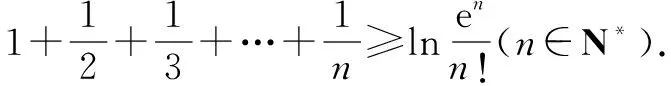
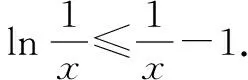
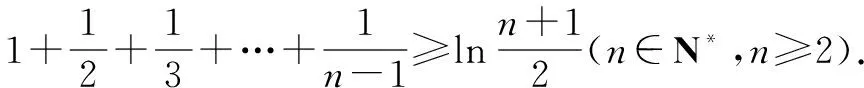
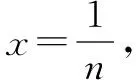
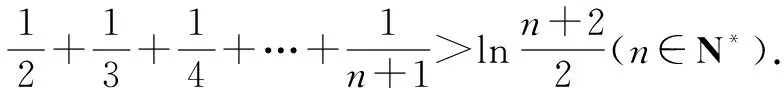
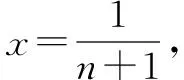
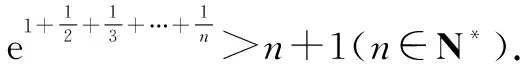
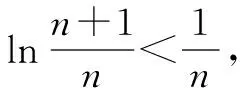
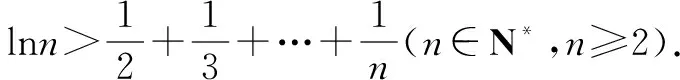
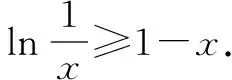
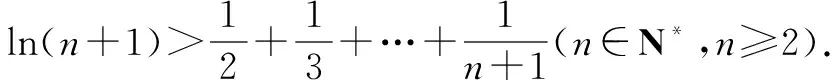
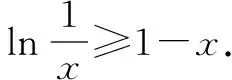
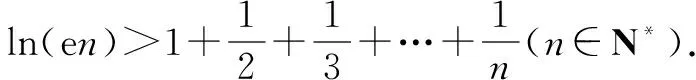
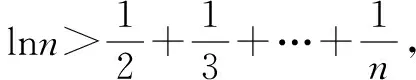

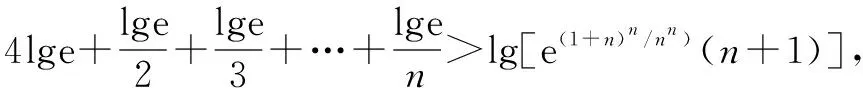
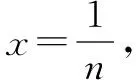
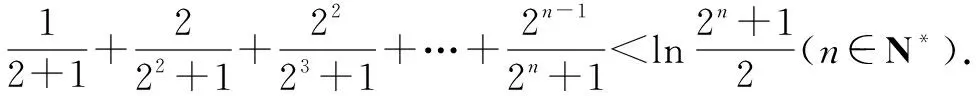
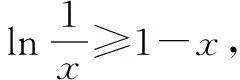
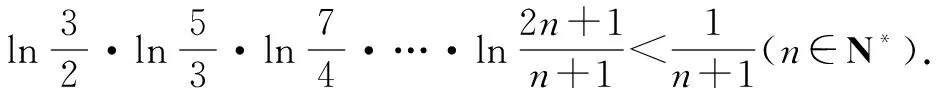
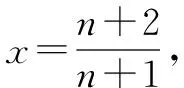
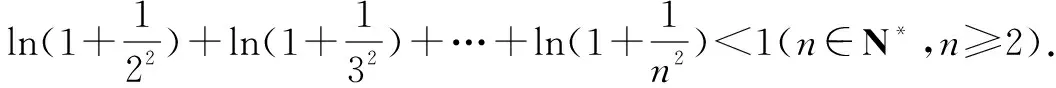
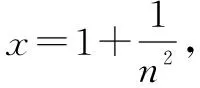

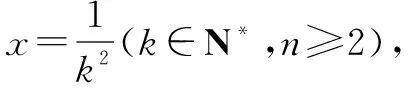
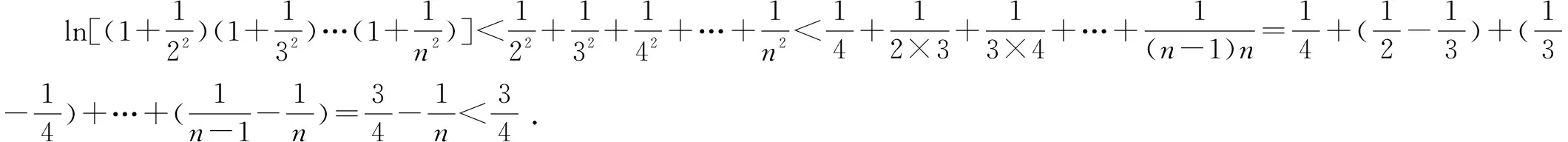

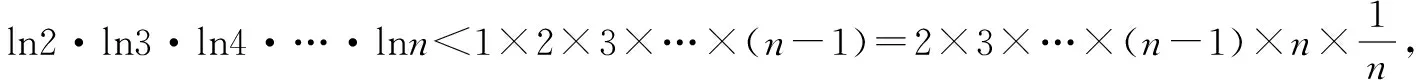
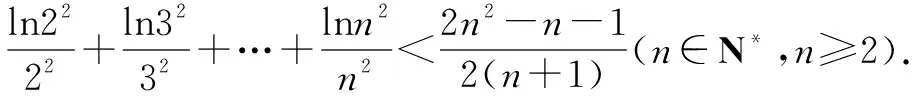
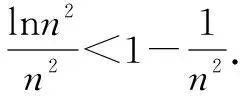
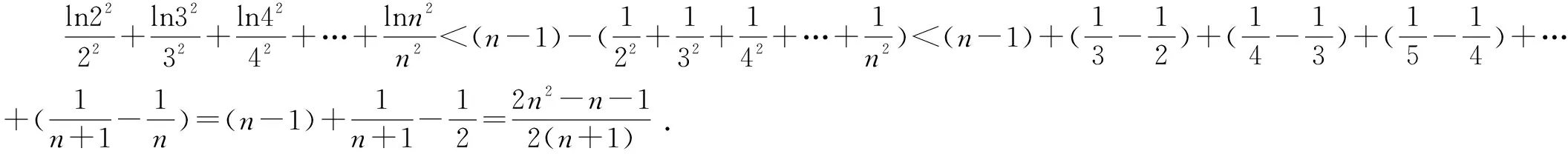
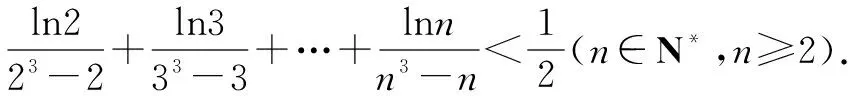
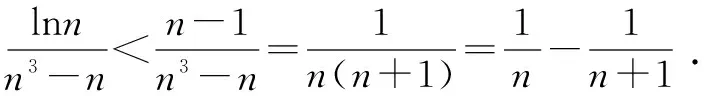

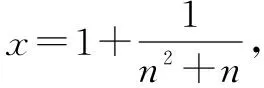
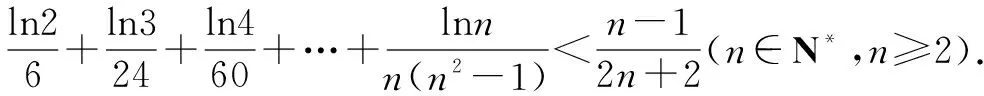
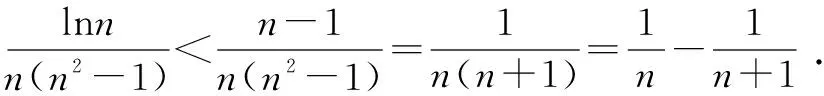
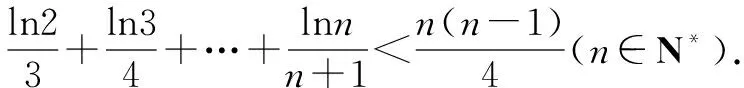
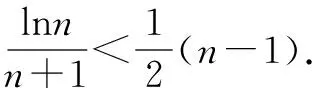
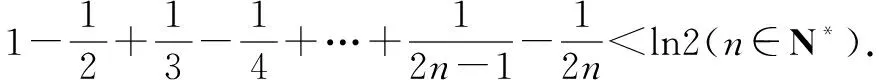
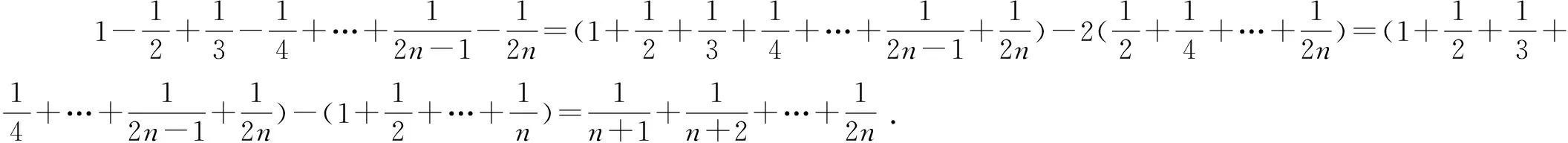
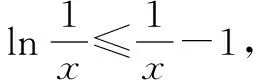
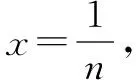
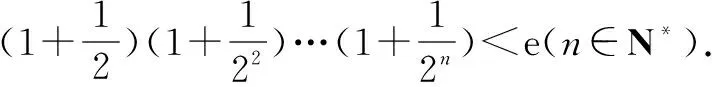
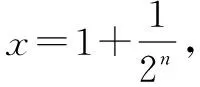
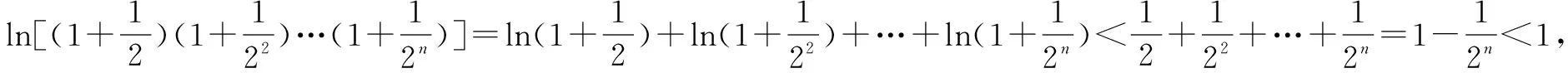
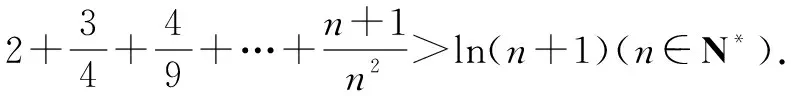
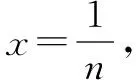
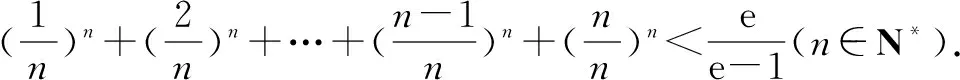
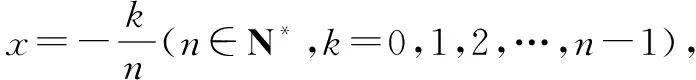
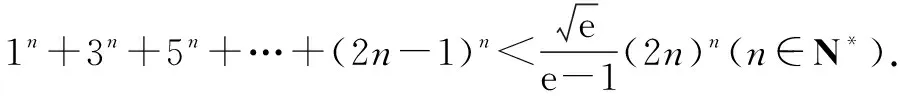
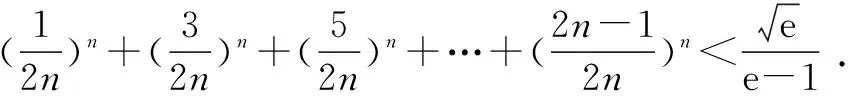
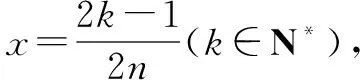
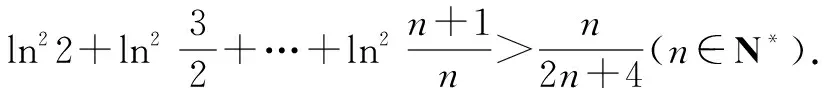
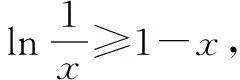
例1至例24中的数列不等式都是从近几年各省市模拟考试数学试卷和高考数学试卷中截取的,具有很高的数学参考及训练价值,所以在这里列举的例题多,大家可以从中领略函数不等式lnx≤x-1(x∈R+)赋值功能的强大和神奇.
导数综合问题在历年高考和各类模拟试题中一般处于压轴题的位置.作为压轴题得分一般都很低,因为有时在推理和运算过程中需要对表达式进行适当的变形与调整,而在很大程度上,这个变形与调整往往是整个题目能否解决的一道分水岭,甚至成为很多学生不可逾越的鸿沟.很多表达式的变形与调整与函数不等式lnx≤x-1(x∈R+)有关,只要我们的学生心里装着函数不等式lnx≤x-1(x∈R+),对函数不等式lnx≤x-1(x∈R+)及其衍生的一些常用函数的组合有较高的敏感度,那么就会使十分困难的表达式的变形与调整变成一件十分自然和水到渠成的事情了.

