一道2020年高考填空题的多维赏析

李昌成 向 前

(1.新疆乌鲁木齐市第八中学 830002；2.新疆乌鲁木齐市第64中学 830017)

有的高考题看上去很朴素，绝大多数考生能顺利完成，好像没有深意.事实上，如果能够深入仔细探究，我们可以发现它的丰富内涵，对我们教育教学有很多启发，对提高学生的数学核心素养有重要的作用，真正意义上避开题海战术，让数学回归到育人的正确轨道上来.下面以2020年全国高考理科数学Ⅰ卷第15题为例，加以研究，以期达到抛砖引玉的效果.

一、试题呈现

二、解法探究

视角1 从直线斜率公式入手，建立关于a，c的关系式.

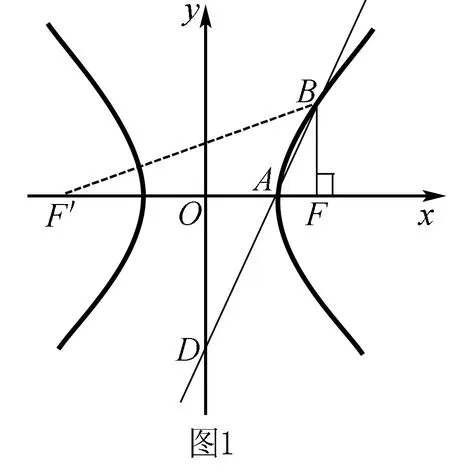
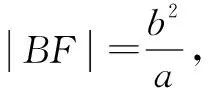
两边同除以a2,得e2-3e+2=0，解得e=2.

评析借助直线的斜率公式，按照通解通法顺利地完成解答，就此罢休可能会错过很多典型教学素材.我们拓宽思路，还会有一些新发现，找到建立关于a，c的关系式更多通解通法，有助于学生形成求解离心率的技能.

视角2 从直角三角形中三角函数入手，建立关于a，c的关系式.

以下同解法1.

评析充分利用解析几何的几何特性，发挥三角函数在代数与几何之间的纽带关系，找到a，c的关系式，这是求离心率问题常见策略.事实上，本解法与解法1具有异曲同工之妙，只是视角不同.

视角3 利用弦长公式和勾股定理，建立关于a，c的关系式.

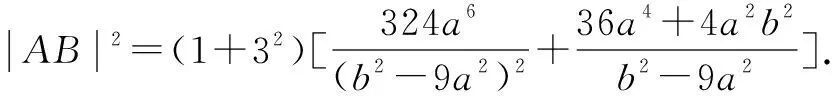
整理得c2+2ac-8a2=0.

进而得e2+2e-8=0.

解得e=2.

评析直线和圆锥曲线的相交关系是高中阶段研究得最深刻的内容之一.该方法容易上手，也能训练学生的数学运算能力.在平时教学中应加强培养，形成能力，同时为应对解答题做好知识技能储备.

视角4 借助同角三角函数关系求弦长，利用勾股定理，建立关于a，c的关系式.

在Rt△ABF中，|AB|2=|AF|2+|BF|2，

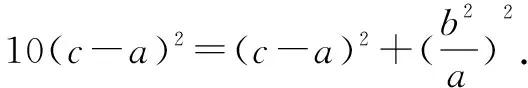
以下同解法3.

评析三角函数将弦长形式简化了，使得后续运算更加简洁明了.这种多模块知识融合解题值得关注，将多模块的知识有机结合起来，体现了知识间的关联性.

视角5 借助相似性，在新三角形中建立关于a，c的关系式.

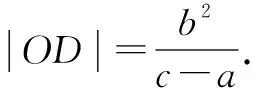
以下同解法1.

评析不同的视角下直线的斜率有不同的比值表达式，但其本质不会改变，为我们提供相互印证的解法，平时多留心，关键时候就不会慌乱，甚至可以快速上手.

视角6 借助双曲线定义，从余弦定理入手，建立关于a，c的关系式.

整理得9c2-18ac+9a2=(c2-a2)2，进一步得9(e-1)2=(e2-1)2，所以(e+1)2=9，解得e=2.

评析在三角形中建立关于a，c的关系式是求离心率的通解通法.利用双曲线的定义确定三角形一条边，利用双曲线的几何量确定一些边，再利用直线斜率确定三角形相关角的三角函数值，使得余弦定理派上用场.这种解法思维流畅，展现了余弦定理的工具性，值得关注.

视角7 利用等面积法，建立关于a，c的关系式.

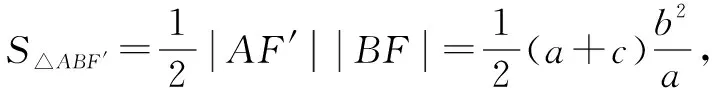
整理得c2-3ac+2a2=0，进而得e2-3e+2=0，解得e=2.

评析等面积法是中学数学中一个重要方法，我们应创造条件加以应用，让重要的方法经常性发挥作用，在潜移默化中形成技能.本法在本题解答中显得新颖，基于约分，运算量也不大，不失为一种妙解.

三、解后反思

求离心率通常可以从代数和几何的角度入手，但是方法不同，思维量不同，运算量不同，可以说不同的方法给带来的“麻烦”不同，解析几何是几何，用几何办法相对简洁.另外，求离心率本质就是找a,c的关系，这是这类题的关键所在.往往a,c关系不明确，需要我们去寻找，去建立，当然入口不唯一，更不容易找到最简洁的一个.我们不仅要教会学生解题，更要注意教会学生在具体问题中，选择最简办法.这是教学质量提升工程，非一日之功.

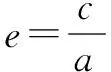
求离心率的问题是一个综合问题，牵涉的面比较广，用到的知识比较多，可用的技巧也丰富，教无定法，学无诀窍，我们只有多思考，多总结，多实战，方可做到得心应手.

潜心研究这么一题，复习了很多知识点，巩固多种技能，让零散的书本知识有机结合起来，不知不觉中又提升了学生的思维水平，训练了学生的计算能力，真可谓一箭多雕.

高考题是我们教学的重要素材，可以从中发现教学的重点和难点.本例中考查的离心率就是高考中的一个重点，也是难点，几乎每年涉及，既有选择题，也有填空题，还有解答题.研究高考题不能仅仅追求答案，更重要的是要深刻理解其考查的知识点，能力要求，本类题的通解通法，通过教学真正培养学生的数学核心素养.研究的关键在于对学生思维的培养和训练，一题多解能避开题海战术，提高教学效率.