平面向量数量积的最值求法分类解析

李秀元

(湖北省武穴市实验高级中学 435400)

平面向量数量积融合了代数、几何及三角等知识，在求其最值时，解题方法呈现出多样性.本文以求最值的主要方式，从六个角度对其进行分类解读，供复习参考.

一、与均值不等式结合

均值不等式是求最值的常用工具之一.要想利用均值不等式，首先得建立基于数量积的等量条件.

例1已知平面向量a，b，c满足|e|=1，a·e=1，b·e=-2，|a+b|=2，则a·b的最大值为( ).

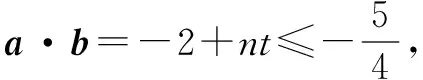
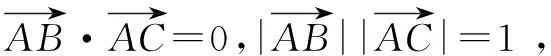
A.13 B.15 C.19 D.21

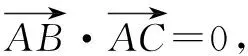
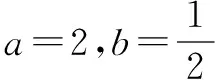
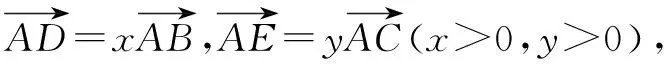
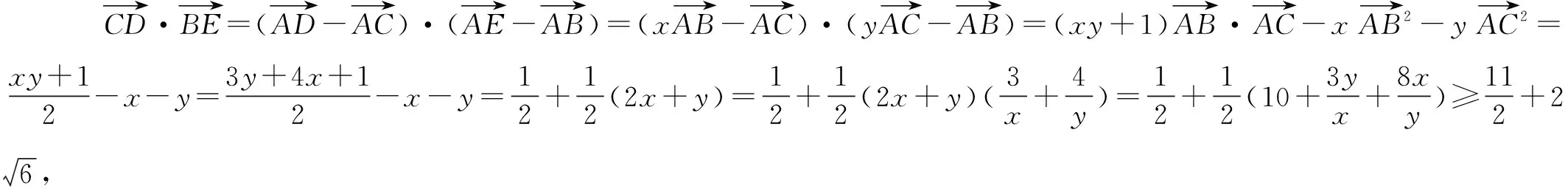
二、与平面几何结合

将平面向量数量积转化为几何图形的某个特征量，主要是想利用平面图形的结构特点来寻找最值，一般会涉及两点之间的距离，点到直线间的距离等.

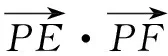
A. [0,24] B. [-12,24]

C. [-8,36] D. [-12,36]

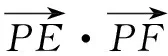
故选D.

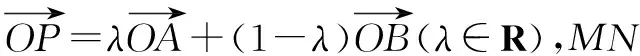
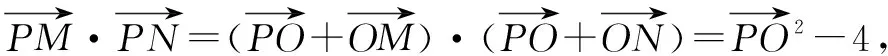
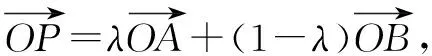
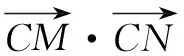
故选A.

三、与线性规划结合

平面向量的数量积与线性规划问题结合，主要有两点，一是由数量积运算得到变量的线性关系，进而将问题直接转化为纯线性规划问题；二是利用数量积运算所得式子的几何意义，巧借可行域的位置，确定最值.由于线性规划内容已不在新课标范围，故仅举一例.

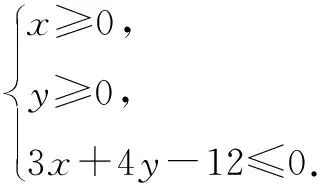
故选A.

四、与二次函数结合

这种题目主要是借助长度，将数量积化归为参数的二次函数形式，利用二次函数的知识求解.

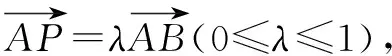
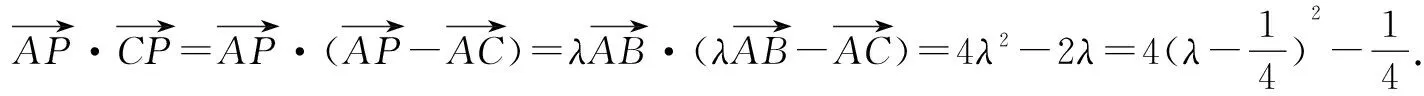
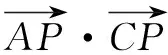
A．[1，4] B．[0，4]

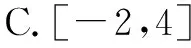
解显然△ABC为直角三角形.设|PA|=m，则|PC|=4-m，且0≤m≤4.

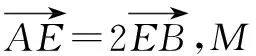
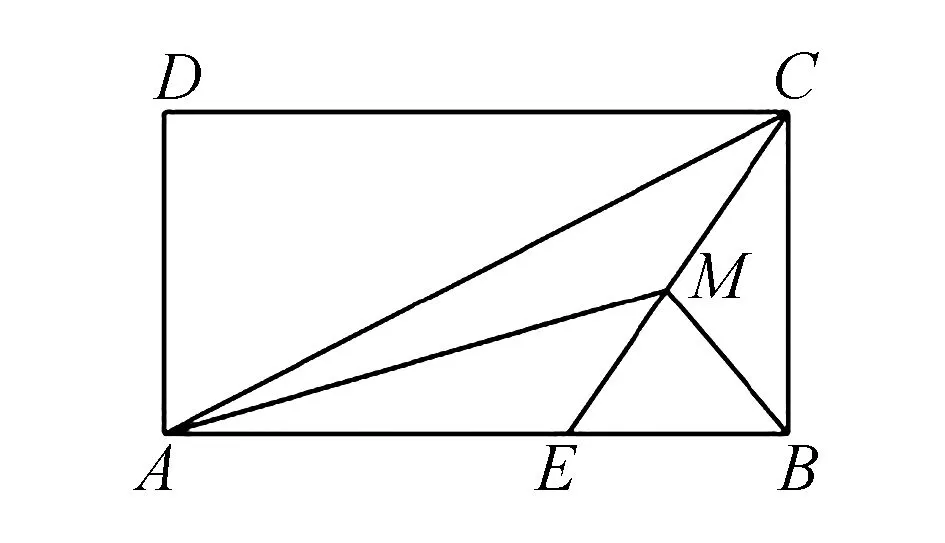
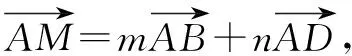
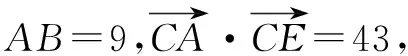
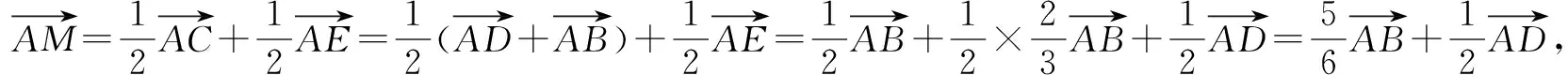
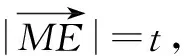
五、与三角函数结合

数量积与三角函数的结合，主要是借助角参数，利用三角函数的诱导公式和恒等变换，以及三角函数的有界性，达到求解的目的.

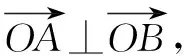
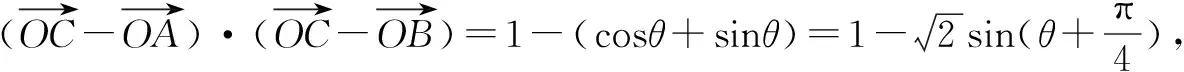
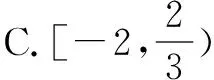
解构造平行四边形ABCD.

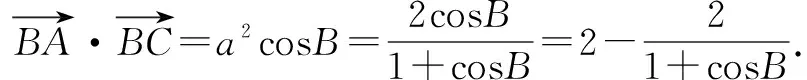
图2

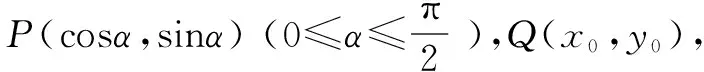
解得x0=1-sinα，y0=1-cosα.

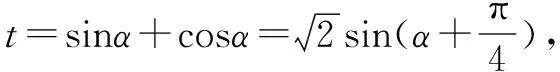
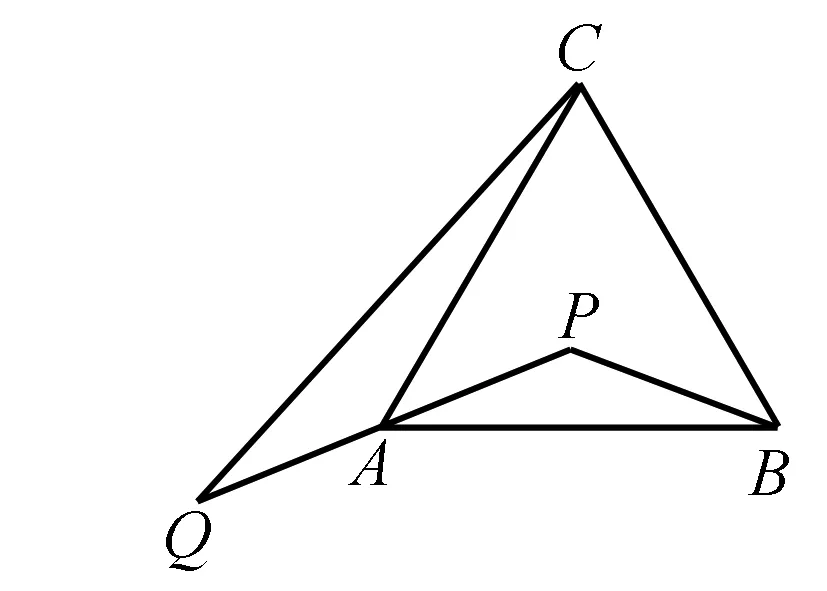
图3

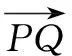
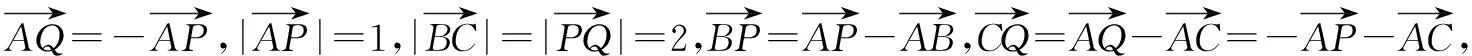
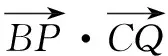
六、与解析几何结合

数量积与解析几何的结合，主要是通过建坐标系，借助数量积的坐标运算，确定目标的指向，然后利用曲线的几何特点来完成问题的解，与直接利用平面几何图形有异曲同工之妙.对于运算后的目标式，一种是针对不受限制的点，主要是利用代数结构求最值，另一种是受几何图形限制的点，则需要结合图形求最值.

图4

例15已知平面向量a，b，c满足|a-b|=6，且(a-c)·(b-c)=-5，则c·(a+b)的最小值为____.

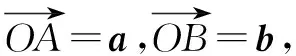
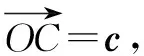
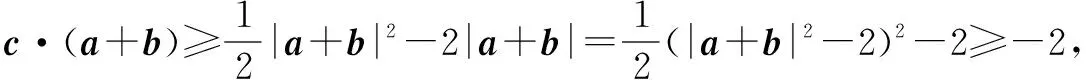
即c·(a+b)最小值为-2．

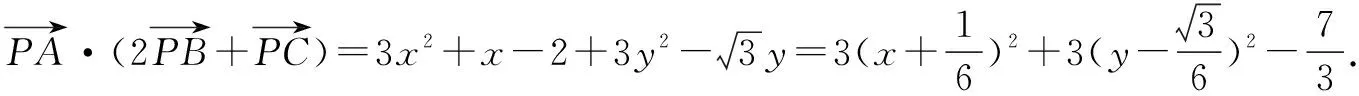
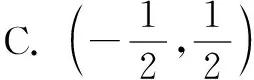
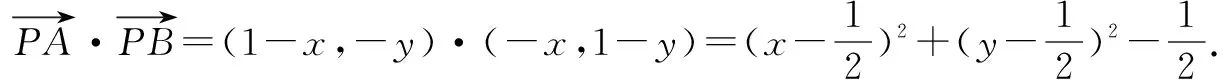
下面这道全国数学联赛省级初赛试题正是基于此设计的，读者可以尝试求解.

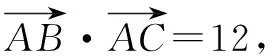
虽然我们将平面向量数量积的最值问题作了些分类，但事实上，它们并不能完全割裂开来，很多时候方法之间是可以转化的，问题是究竟用哪种方式求解更快更方便，如到底需不需要建系，不建系是不是很方便，需要根据题目的条件去权衡，不能死盯着一种方式不放，多方出击，总有一种方法是有效的.