强基计划 你准备好了吗
甘志国
(北京市丰台二中 100071)
一、强基计划介绍
强基计划的前身是大学自主招生(下简称自主招生).
自主招生是我国高校统一考试招生制度的重要补充,也是对学生多元录取、综合评价的重要组成部分.据统计显示,2018年清华北大自主招生、综合评价、高校专项获得降分的总人数,达到了惊人的6100人,占其计划招生总数6700人的91%,详见下表:
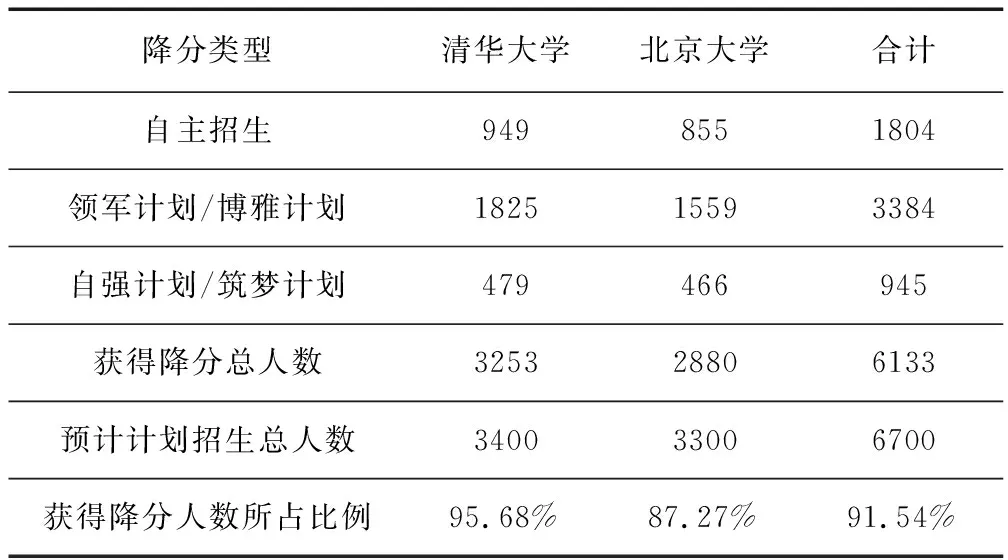
2018年清华北大获得降分人数汇总
从上面的数据可以看出自主招生在扮演非常重要的角色,仅凭裸分考进清华和北大的学生比例已经很低了.
2020年1月14日,教育部以教学〔2020〕1号文件印发《关于在部分高校开展基础学科招生改革试点工作的意见》.文件指出,决定自2020年起,在部分高校开展基础学科招生改革试点(也称强基计划).同时,在部分“一流大学”建设高校范围内遴选高校开展试点.教育部将按照“一校一策”(着重号为笔者所加)的原则,研究确定强基计划招生高校、专业和规模.从2020年起,不再组织开展高校自主招生工作.
二、强基计划考试介绍
很多考生对强基计划试题的难度不太了解,这里做一个粗略的对比.各科综合起来的大致情况是,高考的中档题相当于强基计划简单题,高考难题相当于强基计划中档题也相当于竞赛简单题,强基计划难题相当于竞赛中档题.
可以说,名校强基计划65%的题在课内范围,35%的题是超纲范围(是竞赛题难度,甚至有的题目超过联赛一试).
所以,有人说强基计划试题的难度介于高考和竞赛之间是有道理的.
较为细致的来说,也可以把强基计划试题分为下面三部分:
1.有的题是课内常见的.这类题检查同学们学习基础情况,一般熟练掌握高考内容的同学都能比较容易拿到分.
2.有的题是在高考考纲边缘附近.这类题保留一定数量的高考核心考点,但着力点和区分度主要放在高考自然延伸出的一些知识和方法上.
3.有的题是超出高考考纲的.这类题涉及到课内没学过的知识、公式(比如反三角函数、极限),或者是竞赛联赛经典方法、技巧.
强基计划考试没有考纲,由大学教授、专家或数学界知名人士命题,所以有超纲内容是正常的(当然教授是有出题原则的:应当说,名校强基计划考试题都是好题,对普通高考和全国联赛的复习备考也有重要参考价值).
如果说笔试让名校间接认识了考生,那么面试则是二者的直接碰撞,能否擦出火花直接决定了强基计划考试的最终结果.因此,面试也是名校强基计划考试中十分重要的环节.
三、强基计划考试数学试题特点
目前,高中生在数学思维和数学素养方面表现出诸多不足,比如思维广度不开阔;思路不清晰,对题目的分析不周全,难以准确识别模型以尽快将其转化为相应的数学问题;学生普遍知识面狭窄(如对复数等许多基本知识都不了解);运算能力较低等等;尤其是创新意识和动手操作能力较差.
针对以上情形,强基计划试题便有如下特点.
1.强基计划数学试题突出考查考生的数学思维与数学素养
强基计划的目的是选拔顶尖的优秀人才,所以试题必然会突出这一特点,因为它是各种能力的核心.
题1(2020年上海交通大学自主招生数学试题)已知甲、乙、丙三人的职业是A,B,C之一,且每两个人的职业均不相同.若乙的年龄比C的年龄大,丙的年龄与B的年龄不同,B的年龄比甲的年龄小,则甲、乙、丙三人的职业分别是( ).
A.A,B,CB.C,A,BC.C,B,AD.B,C,A
答案:A.
题2(2020年上海交通大学自主招生数学试题)在小于1000的正整数中,即不是5的倍数也不是7的倍数的整数个数是.
答案:686.
题3(2020年中国科学技术大学创新班初试数学试题第7题)已知函数f(x)=(x-1)2+k2.若a,b,c∈[0,1],f(a),f(b),f(c)是某个三角形的三边长,则k的取值范围是.
注:题1考查逻辑知识(判断命题的真假),题2的解法须用到韦恩图(即容斥原理),解答题3要用到对恒成立问题的处理方法及二次函数在所给闭区间上的最值求法.这些知识、方法都是考生必备的数学素养.
2.强基计划数学试题突出考查思维的广阔性(如发散思维)、深刻性与灵活性

答案:12600.
题5(2020年北京大学强基计划数学试题第6题)已知数列{an}满足a1=1,a2=4,且an2-an-1an+1=2n-1(n≥2,n∈N*),求a2020的个位数.



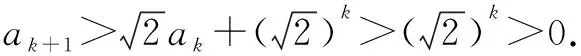
由题设,还可得
得n=k+1时成立,所以欲证结论成立.
由题设,可得
an(2an+an+2)=an+1(2an-1+an+1)(n≥2,n∈N)①.
因为前面已证得an>0(n∈N*),所以
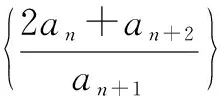
进而可得数列
{an(mod 10)}:1,4,4,8,4,0,2,8,8,6,8,0,4,6,6,2,6,0,8,2,2,4,2,0,6,4,4,8,…
所以an+24≡an(mod 10)(n≥2,n∈N),因而a2020=a24·84+4≡a4=48≡8(mod 10),得a2020的个位数是8.
解法2 先对n用数学归纳法证明:an+2>an+1>an>0,an+2=4an+1-2an(n∈N*).
由a1=1>0,a2=4,a3=14,可得n=1时成立.
假设n=k时成立:ak+2>ak+1>ak>0,ak+2=4ak+1-2ak.
在解法1中得到的①式中,令n=k+1,可得ak+1(2ak+1+ak+3)=ak+2(2ak+ak+2)(ak+1>0),所以
=4ak+2-2ak+1=ak+2+ak+2+2(ak+2-ak+1)>ak+2,
ak+3>ak+2>ak+1>0,
所以ak+3>ak+2>ak+1>0,ak+3=4ak+2-2ak+1,得n=k+1时成立,因而欲证结论成立.
接下来的解法同解法1.
注:题4的解法是用二项展开式的通项解决四项展开式的通项问题,进而求出其常数项,充分考查了思维的广阔性、深刻性与灵活性.
在题5两种解法中,难点均是证明“an≠0(n∈N*)”.这体现了思维的深刻性:蒙混过关是一定会丢分的.
3.许多强基计划试题有深刻背景,可以引申推广

答案:2.

解可设动点A(2cosθ,2sinθ),可得切点弦所在的直线方程是xcosθ+2ysinθ=1.
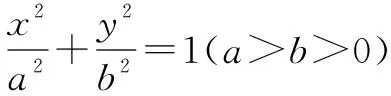

图1
注:题6的背景是《近世代数》中的群、环、域.题7的背景是《高等几何》知识“曲线是切线的包络”:曲线可“点动成线”来生成;也可由曲线上点的切线围成,即“曲线是切线的包络”.
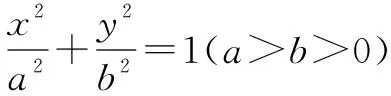
4.强基计划试题覆盖面广
强基计划还没有明确的考试大纲,试题的覆盖面很广,很多题的难度超出高考、联赛,甚至高中数学的知识范围而涉及高等数学,需要考生“见多识广”.
题8(2020年复旦大学强基计划数学试题)若函数f(x)=3x-3-x的反函数为y=f-1(x),则g(x)=f-1(x-1)+1在[-3,5]上的最大值和最小值的和为( ).
A.0 B.1 C.2 D.4
答案:C.

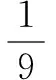

答案:D
题11(2020年复旦大学强基计划数学试题)已知抛物线x=3y2的焦点为F,若该抛物线在点A处的切线与直线AF的夹角为30°,则点A的横坐标为( ).
答案:C.
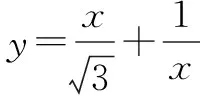

题13(2020年北京大学强基计划数学试题第2题)已知关于x的方程x5+px+q=0有有理根,且正整数p,q均不大于100,求满足这些条件的有序数组(p,q)的组数.
答案:133.
题14(2020年北京大学强基计划数学试题第4题)求方程19x+93y=4xy整数解的组数.
答案:8.
注:解答题8要用到反函数知识,解答题9与题10要用到反三角函数知识,解答题11要用到两直线的夹角公式,题12涉及平面直角坐标系的旋转变换,题13与题14涉及初等数论中的数的整除、不定方程知识.而这些知识在现行高中数学教材中均未讲述,但属于强基计划的命题范围.
5.部分数学强基计划试题运算量较大,或有较强的技巧
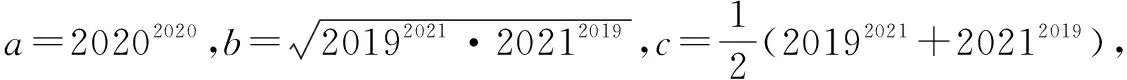
答案:c>a>b.
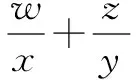

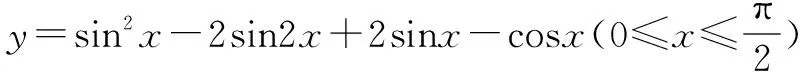

题18 (2020年中国科学技术大学创新班初试数学试题第10题)已知函数f(x)=x3+ax2-x+1-a,若∀x∈[-1,1],|f(x)|≥|x|,求实数a的取值范围.

注:解答题15与题16均需要用到较强的放缩技巧,后者还要使用导数;解答题17需要用到较强的凑配技巧:先得y=(2sinx-cosx)2+(2sinx-cosx)-1,再用换元法求解(这与高中三角函数题的常规解法不一样);题18是所在试卷(共11道试题)难度最大的一道试题,其常规解法须用到二次讨论,比较复杂.
6.强基计划数学试题注重引导培养考生创新意识和动手操作能力
毫无疑问,这是强基计划考试的主旨与方向.
题19(2020年上海交通大学自主招生数学试题)对于方程2x-sinx=1,在下列结论中错误的序号是:
(1)该方程无正数根;
(2)该方程有无数个根;
(3)该方程有一个正数根;
(4)该方程的实根小于1.
答案:(1).
题20(2020年复旦大学强基计划数学试题,原题为单项选择题)若k>4,则直线kx-2y-2k+8=0和2x+k2y-4k2-4=0与两条坐标轴围成的四边形面积的取值范围是____.

题21(2020年上海交通大学自主招生数学试题)单位正方体的六边形截面周长的最小值是____.
注:解答题19须使用图形计算器(上海的数学高考是允许的),否则本题难度很大;题20的解法是准确作图后用割补法及配方法求解;题21的解法是用正方体的平面展开图来求解.
7.部分数学强基计划试题解法简洁新颖,用到知识也很少
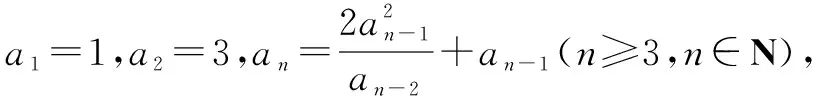
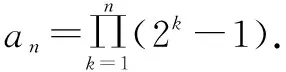
注:解答本题只需用到构造法与累乘法.
8.数学强基计划试题的最大特点是原创性
由于强基计划试题命题人多是大学教授、专家或数学界知名学者,他们视野宽阔,经常站在数学学科和社会发展的前沿思考问题,因此每年的自主招生试题都令人耳目一新,难以捉摸;但仔细分析一些强基计划数学试题,还是可以看出其一些特点的,而原创性是其最明显特点.
四、强基计划考试数学试题的来源
1.源于教材
教材是命题的基本依据,不少强基计划试题有教材背景,是教材上例题、习题、定义、定理的组合改编,甚至有时就是原题.
题23(2020年上海交通大学自主招生数学试题)用同样大小的正n边形平铺整个平面(没有重叠且没有空隙),若要将这个平面铺满,则n=____.
答案:3,4,或6.

答案:均不存在.
注:初中数学教材中就有题23这类平面平铺问题.

2.源于国内外高考试题
许多稍难的高考试题更适合更高层次的选拔,所以有些这样的高考题就被改编成了(或直接作为)强基计划试题.
题25 (2020年上海交通大学自主招生数学试题)若某个四面体的各个顶点到某个平面的距离都相等,则称该平面为这个四面体的中位面.一个已知的四面体的中位面的个数是____.(答案:7.)
题26(2020年上海交通大学自主招生数学试题)与两两异面的三条直线均相交的直线条数是____.(答案:无数.)
注:题25是空间距离中的经典问题;作为排列组合知识,还涉及均匀分组和非均匀分组.这道题与2005年高考全国卷Ⅲ文科、理科第11题实质相同.
不共面的四个定点到平面α的距离都相等,这样的平面α共有( ).
A.3个 B.4个 C.6个 D.7个
题26与下面的两道题目实质相同:
(2008年高考辽宁卷理科第11题即文科第12题)在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( ).
A.不存在 B.有且只有两条
C.有且只有三条 D.有无数条
(复旦大学2008年自主选拔数学B卷试题第26题)若空间三条直线a,b,c两两异面,则与a,b,c都相交的直线有( ).
A.0条 B.1条
C.多于1条的有限条 D.无穷多条
3.源于历年的强基计划(自主招生)试题

答案:0.
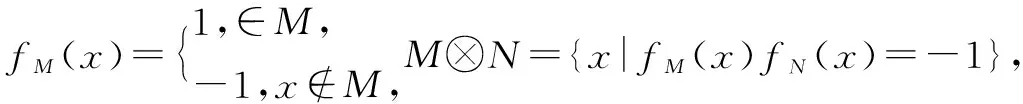
答案:(-∞,-3]∪[0,1)∪(3,+∞).


题30 (2020年中国科学技术大学创新班初试数学试题第2题)点集{(x,y)||5x+6y|+|9x+11y|≤1}的面积是____.
答案:2.
注:题27,28,29,30分别与下面的自主招生试题如出一辙.

A. -121 B. -49 C. 0 D.23
答案:C.
(1)求fA(2016),fB(2016);
(2)设card(X)表示集合X的元素个数,求m=card(XΔA)+card(XΔB)的最小值.
答案:(1)-1,-1;(2)2016.
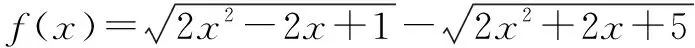

(2019年中国科学技术大学自主招生数学试题第1题)满足|x+2y|+|3x+4y|≤5(x,y∈R)的点(x,y)所构成的区域的面积是____.
答案:25.

4.源于各级各类竞赛试题

A.0 B.1 C.-1 D.与a有关
答案:B.
注:该题源于早年的数学竞赛试题:用减函数与单调函数的性质求解.
5.源于某些初等数学研究成果
题32 (2020年中国科学技术大学创新班初试数学试题第8题)已知a1,a2,…,an是1,2,…,n的一个排列,若i 注:该题的背景是《高等代数》中排列的顺序数、逆序数.拙著《初等数学研究(Ⅰ)》第509-512页的文章《12…n的所有m元排列的反序数之和及其应用》研究了该题的一般情形. 6.源于高等数学 前面已述,题7(2020年北京大学强基计划数学试题第3题)源于《高等几何》知识“曲线是切线的包络”,题32源于《高等代数》中排列的顺序数、逆序数. 答案:(1,2). 注:题33源于《高等代数》中的行列式,题34源于定积分. 考生在日常学习中应该重新审视高考中“不常考”的知识和方法,并做必要的拓展,增强对数学问题的探究意识,关注高中数学后续内容的学习,注重数学思想方法的学习和创造性思维的培养,细述如下. 1.夯实基础,尤其要自觉加强基本运算能力的训练 千里之行,始于足下;强化基本功训练,是今后延拓知识与快速提高素养的资本! 解答强基计划数学试题用到的思想、方法和知识,大部分也都在高考范围之内.因而,准备高考和准备强基计划应该是相辅相成,互相补充的. 2.注重知识的延伸与拓展 题35 (2020年复旦大学强基计划数学试题,原题为单项选择题)如图2所示,平面内两条直线l1,l2交于点O,M为该平面内的任意一点.若点M到直线l1,l2的距离分别为p,q,则称(p,q)是点m的“距离坐标”.p,q是已知的非负常数,给出下列三个结论: (1)若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个; (2)若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个; (3)若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个. 其中正确结论的个数是( ). A.0 B.1 C.2 D.3 答案:D. A.8 B.7 C.6 D.6或7 解D.由题设,可得 所以当且仅当n=6或7时,Sn取到最大值. 注:题35中的“距离坐标”是平面直角坐标系中点的坐标的一种推广,但两者的本质均是平行线的距离;题36仅仅是把考生在高中阶段学习的两个、三个向量的和推广到n个向量的和而已. 在日常学习中,不能仅仅局限于教材,要学得更深更广: (1)注重在不同的知识阶段及时延伸与拓展. 比如学习函数时,不仅要学习函数的定义、基本性质及各类基本初等函数,还要及时学习函数与方程的思想方法.这有助于对函数理解得更深刻,在更为高级的层面上构建知识结构和认知结构. (2)关注AP课程及其他多种形式的学习. AP课程中的许多内容和方法已经进入强基计划试题,如极限理论中的数列收敛准则、夹逼定理、函数极限存在定理、迫敛性定理、两个重要极限、洛比达法则,微积分中的罗尔定理、拉格朗日中值定理、积分中值定理、牛顿-莱布尼茨公式等等. 强基计划试题的风格与难度,和高考还是有较大的不同.同时强基计划也会考一些在高考范围边缘处的知识.既没有接触过竞赛,又没有准备过强基计划的裸考考生最终很可能会无功而返. 3.注重数学思想方法的领会与运用 题37 (2020年上海交通大学自主招生数学试题)从2个相同的红球、3个相同的黑球、5个相同的白球中取出6个球,共有____种不同的取法. 答案:11. 答案:a,b,c,d. 注:题37的解法是枚举法;题38的解法是赋值法,其理论依据是“特殊与一般思想”;解答前面的题28要用到等价转化思想与分类讨论思想.这些思想方法都是考生必备的数学素养. 4.培养推广与探究的意识 这是研究问题的重要方法:解一题,知一类. 题39(2020年复旦大学强基计划数学试题)方程3x+4y+12z=2020的自然数解的组数为____. 解C.可设x=4m(m∈N),得原方程即3m+3z+(y-1)=3·168(m,y,z∈N);可再设y=3n+1(n∈N),得原方程即m+n+z=168(m,n,z∈N). 可设m=m′-1,n=n′-1,z=z′-1(m′,n′,z′∈N*),得原方程即m′+n′+z′=171(m,′n′,z′∈N*).再由隔板法,可得所求答案是C. 注:考生应当通过推广与探究,最终理解隔板法是解决一次不定方程正整数、自然数解组数的通性通法. 5.留心跨界科学与学科知识的交汇 题40(2020年复旦大学强基计划数学试题)Given two setsA:{1,2,3,4,5}andB:{3,4,5,6,7},then the intersection set ofAandBis( ). A.{1,2} B.{3,4,5} C.{1,2,3,4,5,6,7} D.{6,7} 答案:B. 题41(2020年复旦大学强基计划数学试题)Which number that number 5 is the cubic root of( ). A.3 B.5 C.25 D.125 答案:B. 注:解答这两道题时,考生对数学专业的英语词汇(交集、立方根等)要过关.复旦大学的强基计划(自主招生)试题历来重视通识教育,这从复旦“千分考”可见一斑:“千分考”测试的内容涵盖高中语文、数学、英语、政治、历史、地理、物理、化学、生物和计算机共10个科目,共计200道选择题,满分1000分(每题答对得5分,不答得0分,答错扣2分),考试时间为3小时. 6.培养自主学习能力 题42(2020年上海交通大学自主招生数学试题)若△ABC的三个顶点的坐标分别是A(3,4),B(6,0),C(-5,-2),则∠A的平分线所在的直线方程是____. 所以∠A的平分线所在直线的一个方向向量是(1,7),因而该直线的斜率是7,进而可得该直线的方程是y-4=7(x-3)即7x-y-17=0. 题43(2020年上海交通大学自主招生数学试题)在正方体的8个顶点中的任意两点确定的直线中,异面直线的对数是____. 答案:174. 注:题42还可用三角形的角平分线性质定理,或解三角形知识求解,或先得出∠BAC=90°后再求解,但运算量都要大一些;题43的解法是先构造四面体,再由“每个四面体确定3对异面直线(即3对对棱所在的直线)”来求解;可用换元法求解第44题:在三个式子sinxcosx,sinx+cosx,sinx-cosx中,只要知道任一个式子的值,就可用换元法并利用恒等式“sin2x+cos2x=1”求出另外两个式子的值. 实际上,这些的解法均是通性通法.但这些通性通法在资料中并不多见,老师也很可能不会讲到.需要考生通过自学获得. 考生应当时刻培养自主学习能力:二十一世纪最重要的个人能力首推自主学习能力!有了过硬的自学能力和意识,即可与时俱进,也可从容应对很多新问题. 参加强基计划对于大学和考生来说,是个双赢的过程.考生要想如愿考上顶尖名校,参加强基计划是一条捷径.笔者认为,强基计划会持续受到家长及学生、学校(高中、高校)、社会的高度关注. 经过以上论述,读者(考生)可能对强基计划及其数学试题有了比较全面深入的了解,希望你提前做好规划、及时行动、充分应变,并在做中体味、修正、总结、提高. 注:本文摘自《高考数学强基计划备考的策略与方法》(包括高一、高二、高三共三个分册)(陕西师范大学出版总社,2020)的《序》.

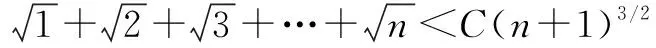
五、大学强基计划数学试题的备考策略






六、强基计划数学考试备考规划

