半群CIn 的秩

吕 会， 罗永贵， 赵 平*

（1.贵州师范大学 数学科学学院，贵州 贵阳550025； 2.贵阳市清华中学，贵州 贵阳550025）

设［n］=｛1，2，3，…，n-1，n｝（n≥3）并赋予自然数的大小序.PTn是［n］上的部分变换半群，令POn=｛α∈PTn：x，y∈dom（α），x≤y⇒xα≤yα｝，称POn为保序部分变换半群.In是［n］上的一一变换半群，称POIn=POn∩In为保序部分一一变换半群，记SPOIn=POIn＼Sn，称SPOIn为保序严格部分一一变换半群. Sn是［n］上的对称群，记S In=In＼Sn，则S In是In的子半群，称S In为奇异一一变换半群.对任意的α∈S In，ker（α）=｛（x，y）∈［n］×［n］：xα=yα｝和im（α）分别表示α的核和像集.设S是有限变换半群，A是S的子集，则〈A〉表示半群S的由A生成的子半群.若半群S的子集A满足〈A〉=S，则称〈A〉为S的生成集.

通常，一个有限半群S的秩定义为

变换半群秩的相关研究一直以来都是半群理论研究中的热点之一［1-8］.文献［1］研究了［n］上的奇异一一变换半群的SPn的秩和幂零秩为n+1.文献［2］证明了一一变换半群的理想I（n，r）=｛α∈In：|im（α）|≤r｝的秩为Cnr+1.文献［3］研究了半群Tn=Sn∪Singn的生成元和秩.文献［4］研究了一些部分变换半群的最小相关生成集，并证明了半群A（n，r）=An∪Tn，PA（n，r）=An∪PTn（An是［n］上的正交群，PT（n，r）=｛α∈PIn：|im（α）|≤r｝，1≤r≤n，PTn是Xn上的部分变换半群）的相关秩.

设

则Cn=〈g〉为g生成的循环群.记CIn=Cn∪S In.本文在文献［1 - 8］的基础上继续考虑新半群CIn=Cn∪S In的秩，证明了如下主要结果.

定理设n为自然数，则

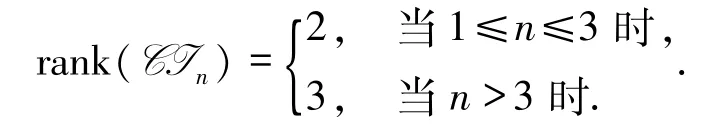
本文未定义的术语及符号参考文献［9 -10］.

1 预备知识

为了方便起见，用符号

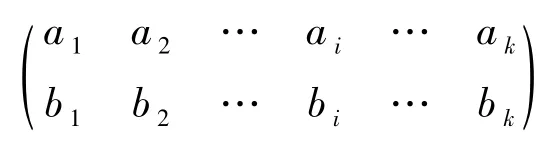
表示半群CIn中满足以下条件的元素α：

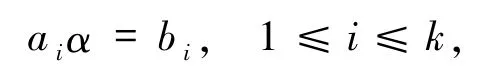
xα=Ø，x∈［n］＼（a1∪a2∪…∪ak）.在CIn上引入如下二元关系，对任意α，β∈CIn有：α R◇β当且仅当ker（α）=ker（β），αL◇β当且仅当im（α）=im（β），α J◇β 当且仅当|im（α）| =|im（β）|.令H◇= L◇∩R◇，易见，R◇、L◇、J◇与H◇都是半群CIn上的等价关系，H J◇=L◇∩R◇，对任意的α∈CIn，记

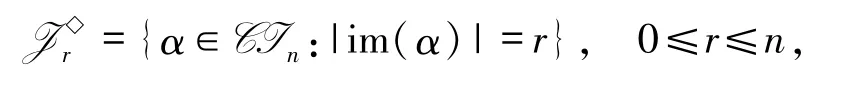
用Xn（n-1）表示自然序集［n］（n≥3）的所有n-1 元子集，则Xn（n-1）中共有n个元素.

记Xn（n-1）=｛Z1，Z2，…，Zn-1，Zn｝.为了方便，假设：

2 定理的证明

为了完成定理的证明，先给出若干引理与推论.文中凡是整数（Z）的加法运算，均是在模n的剩余类环中进行的，例如n+i=i.

引理1对n≥3，有

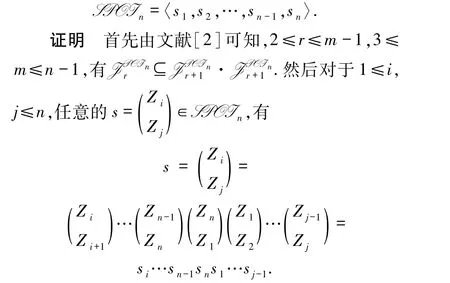
引理2对任意的α，β∈CIn，若（α，β），（α，αβ）∈J◇，则（α，αβ）∈R◇且（αβ，β）∈L◇.

证明若（α，β），（α，αβ）∈J◇，则

再由im（αβ）⊆im（β），ker（α）⊆ker（αβ）与［n］的有限性知，im（αβ）=im（β），ker（α）=ker（αβ），即（α，αβ）∈R◇，（αβ，β）∈L◇.

引理3设n≥3，S In=〈s1，s2，…，sn-1，＾sn，s0〉.

证明首先由文献［2］可知，2≤r≤m-1，3≤m≤n-1，有Jr◇⊆Jr+1◇·Jr+1◇.

然后

时，其中：

1）i1≠0，sp≠0 时，j1与tq可能等于0，可能不等于0，其中若j1=0 时，t1≠0，若tq=0 时，jq≠0，共4 种情形；

2）i1≠0，sp=0，ip≠0 时，j1与tq可能等于0，可能不等于0，其中若j1=0 时，t1≠0，若tq=0 时，jq≠0，共4 种情形；

3）i1=0，s1≠0，sp≠0，时，j1与tq可能等于0，可能不等于0，其中若j1=0 时，t1≠0，若tq=0 时，jq≠0，共4 种情形；

4）i1=0，s1≠0，sp=0，ip≠0，时，j1与tq可能等于0，可能不等于0，其中若j1=0 时，t1≠0，若tq=0时，jq≠0，共4 种情形.

先考虑其中1 种情形，若

易验证其他情形和以上一样.

易知n＞3 时，有στ≠τσ成立，则

推论2当1≤n≤3 时，rank（CIn）=2.

定理的证明由引理3 与引理5 可知，当n≥3时，rank（CIn）≤3.再由推论2 知，当1≤n≤3 时，rank（CIn）=2.由引理7 知，当n＞3，rank（CIn）≥3.因此，结合推论1 与引理5，当n为自然数时，有