邻域概率粗糙集的不确定性度量
周艳红, 张 迪, 莫智文
(1.中国民用航空飞行学院 计算机学院,四川 广汉618307; 2.四川师范大学 智能信息与量子信息研究所,四川 成都610066)
粗糙集理论作为一种数据分析处理的理论[1],在知识获取、机器学习和数据挖掘等领域有广泛应用[2].在粗糙集理论中,不确定性度量是描述系统分类能力的重要依据,对此很多学者进行了相关研究[3-6].Pawlak[3]提出3 种不确定性度量,即精度、粗糙度和近似精度;文献[4]通过引入知识粒度,提出基于知识粒度的精度、粗糙度和近似精度;文献[5]研究了关于粒的不确定性度量及其关系;文献[6]在概率粗糙集模型中揭示了3 种经典不确定性度量(即精度、粗糙度和近似精度)的局限性,提出基于期望粒度的3 种单调不确定性度量,为属性约简奠定良好的基础.
经典粗糙集主要采用等价关系和等价类,在应用时需要对相关的数值数据进行离散化,具有局限性.为此,文献[7]提出比等价关系更为通用的邻域关系,并广泛应用于不确定性数据的特征提取、属性约简等[8-13].在邻域系统中,不确定性度量对属性约简具有重要作用.文献[8]提出邻域熵、信息粒、基于邻域熵的近似精度等多种不确定性度量,并研究其相关性质;文献[9]在邻域粗糙集中提出邻域精度、粗糙度及近似精度.
由于经典的邻域粗糙集模型对噪声的容忍性相对较差,为此,主要对邻域粗糙集模型进行扩展.首先,通过引入2 个阀值,构造出邻域概率粗糙集模型,提出3 种不确定性度量;再次,将邻域概率粗糙集和邻域粗糙集相结合,提出3 种改进的不确定性度量.
1 邻域粗糙集
主要介绍邻域粗糙集中一些基本的概念[8,10,14].设NIS=(U,C,V,f,δ)是一个信息系统,其中,U={xi|i=1,…,n}为非空有限集;C是非空属性集;V为所有属性的值域,即表示属性c所有可能取值的集合);δ∈[0,1]为邻域参数.定义NDS=(U,C∪D,V,f,δ)是邻域决策信息系统,其中C和D分别表示系统的条件属性和决策属性.U/D={X1,X2,…,Xm}是决策属性D在U上的一个等价类.
关于属性子集A={a1,a2,…,a|A|}的距离函数为
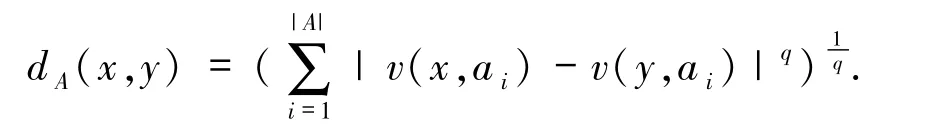
其中,q=1 时,dA(x,y)为Manhattan距离;q=2 时,为Euclidean 距离;q=∞时,为Chebychev 距离.本文采用Manhattan距离.由dA和δ产生邻域(类)为
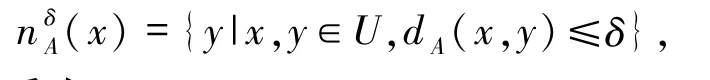
邻域关系为
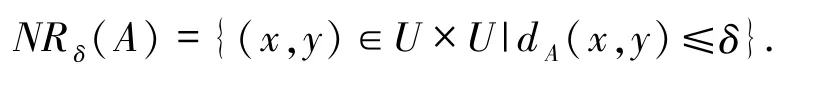

2 邻域概率粗糙集的不确定性度量
在邻域粗糙集基础上,本节通过引入2 个阀值,提出邻域概率粗糙集模型,并逐步构建出3 种改进的不确定性度量.
2.1 3 种邻域概率不确定性度量及其单调性通过引入2 个阀值,提出邻域概率粗糙集模型,定义3种不确定性度量,即邻域概率精度、粗糙度和近似精度,并研究这3 种不确定性度量的单调性.
定义2 在NIS中,0≤β <α≤1,A⊆C,X⊆U,则X关于A的邻域概率下、上近似为:
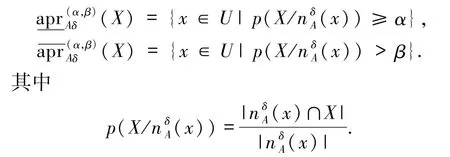
在NDS中,A⊆C,U/D={X1,X2,…,Xm},则U/D关于A的邻域概率下、上近似为:
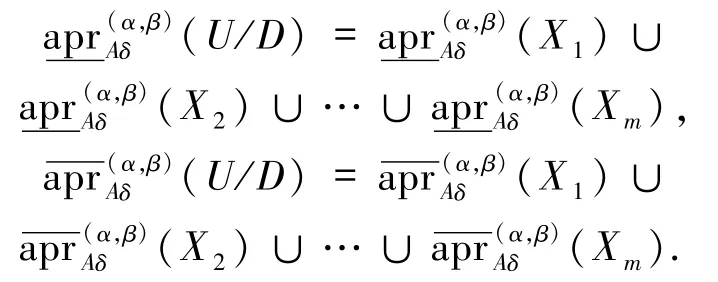
定义3在NIS中,0≤β <α≤1,A⊆C,X⊆U,则X关于A的邻域概率精度和粗糙度分别为:
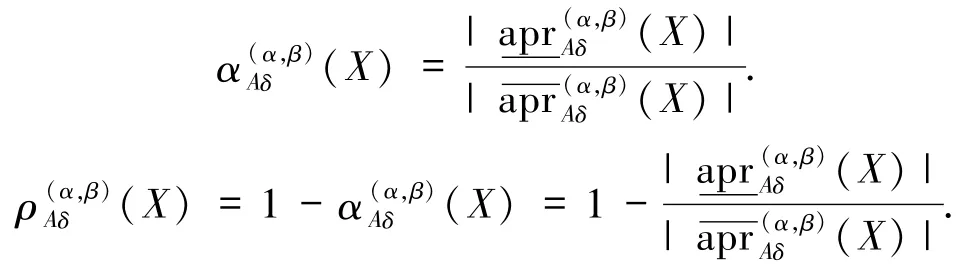
定义4在NDS中,0≤β <α≤1,A⊆C,则U/D关于A的邻域概率近似精度为
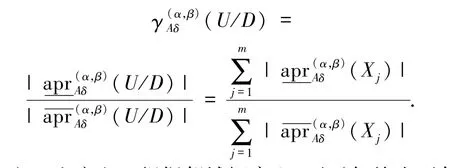
定义3 和定义4 根据邻域概率上、下近似给出了邻域概率精度、粗糙度和近似精度的概念.
对比文献[6]中概率粗糙集中的概率精度、粗糙度和近似精度,本节所定义的邻域概率粗糙集中的概率精度、粗糙度和近似精度更具有一般性,即推论1.
推论1NIS中,若δ=0 时,则有:

推论1 表明在δ =0 时,邻域概率粗糙集退化为概率粗糙集,即邻域概率粗糙集是概率粗糙集的推广,更具有一般化.
下面主要通过例1 讨论其单调性.
例1设NDS=(U,C∪D,V,f,δ)如表1.

表1 例1 决策表Tab. 1 Decision table of Example 1
表1 中,U={x1,x2…,x6},C={a1,a2,a3},U/D={X1,X2}={{x1,x4,x6},{x2,x3,x5}},α =0.4,β=0.3,δ=0.4.
选取B={a1},A={a1,a2}和C={a1,a2,a3}.首先计算A所对应的邻域类,即


表2 例1 中粒度粗化过程中的邻域类Tab. 2 Neighborhood classes during granularity coarsening in Example 1
根据表2,由定义3 和4 分别计算出邻域概率精度、粗糙度和近似精度所对应的值,结果如下:

从例1 中说明邻域概率精度、粗糙度和近似精度不具备单调性,即
1)在NIS中,0≤β <α≤1,B⊆A⊆C,X⊆U,下列结论不成立:

2)在NIS中,0≤β <α≤1,B⊆A⊆C,X⊆U,下列结论不成立:

由于例1 中所涉及的粗化过程较少,邻域概率近似精度的非单调性并未完全体现,其结果将会在UCI数据实验中充分体现.
2.2 3 种改进邻域概率不确定性度量及其单调性在粗化过程中,由于邻域概率粗糙集中的上下近似不具备单调性.因此,邻域概率粗糙集中的精度、粗糙度和近似精度也不具备单调性,进而需要对邻域概率精度、粗糙度和近似精度进行改进,使其满足粒化单调性,即为改进的邻域概率精度、粗糙度和近似精度,并讨论相关性质.下面通过结合邻域粗糙集的上下近似,建设性地提出改进的邻域概率精度、粗糙度及近似精度,并对单调性进行研究.
定义5在NIS中,0≤β <α≤1,A⊆C,X⊆U,则X关于A的改进邻域概率精度和粗糙度分别为:

定义6在NDS中,0≤β <α≤1,A⊆C,X⊆U,U/D={X1,…,Xm},则U/D关于A的改进邻域概率近似精度为
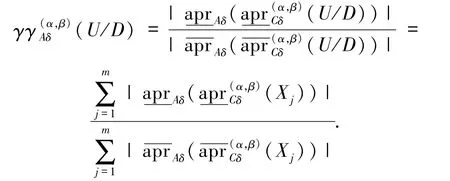
定义5 和定义6 将邻域概率粗糙集和邻域粗糙集相结合,分别提出了改进的邻域概率精度、粗糙度和近似精度的概念.下面主要讨论其单调性.立,性质3 说明改进的邻域概率精度、粗糙度具有参数单调性.
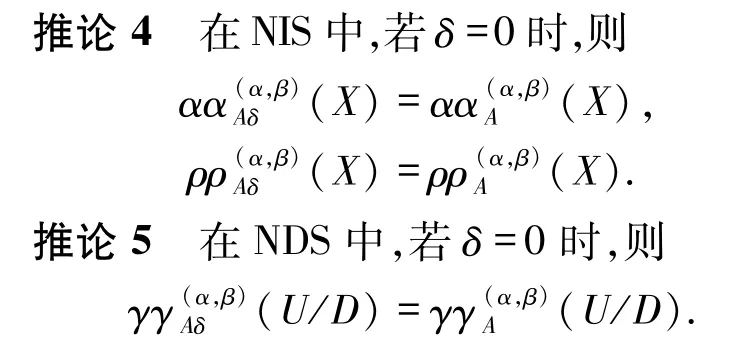


由推论4 和推论5 看出,文献[6]在概率粗糙集中所提出的概率精度、粗糙度和近似精度是改进邻域概率精度、粗糙度和近似精度的一种特例.
下面通过例2 对改进邻域概率精度、粗糙度和近似精度单调性进行验证说明.
例2利用定义5 和定义6,通过计算,其改进的邻域概率精度、粗糙度和近似精度的值如表3.

表3 3 种改进邻域概率不确定性度量的值Tab. 3 Values of three improved neighborhood probabilistic uncertainty measures
在粒度粗化过程中,3 种改进的邻域概率不确定性度量具有明确的单调性.例如,针对例1 选取的粗化过程“{a1,a2,a3}→{a1,a2}→{a1}”,改进邻域概率精度、粗糙度和近似精度分别表现为:
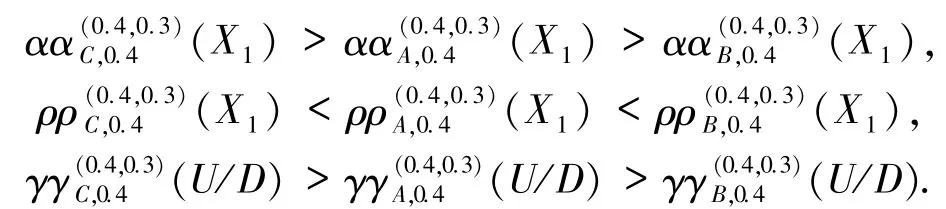
对比例1,改进的邻域概率精度、粗糙度和近似精度具有单调性,改良了邻域概率粗糙集中邻域概率精度、粗糙度和近似精度的非单调性.
3 UCI数据实验
主要选取2 种UCI数据进行实验,对本文所提出的邻域概率精度、粗糙度和近似精度以及改进的邻域概率精度、粗糙度和近似精度的非单调性/单调性进行比较分析.
数据实验包含2 组数据,具体为:wdbc 数据集包含569 个对象,30 个条件属性(只取前12 个),1个决策属性(U/D={X1,X2}),取δ=0.3,α=0.4,β=0.3;sonar数据集包含208 个对象,60 个条件属性(只取前11 个),1 个决策属性(U/D={X1,X2}),取δ =0.05,α =0.4,β =0.3.实验结果如图1 -10 所示.为方便,将邻域概率精度、粗糙度和近似精度分别简记为PNA、PNR、PNAA以及改进的邻域概率精度、粗糙度和近似精度分别简记为MPNA、MPNR、MPNAA.

图1 2 种邻域概率精度(wdbc,δ=0.3,X1)Fig. 1 Two kinds of neighborhood probabilistic accuracies(wdbc,δ=0.3,X1)
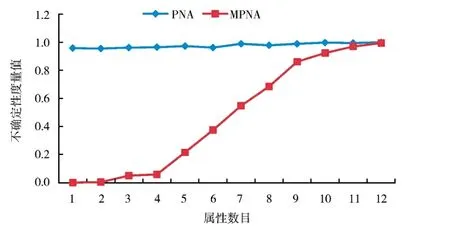
图2 2 种邻域概率精度(wdbc,δ=0.3,X2)Fig. 2 Two kinds of neighborhood probabilistic accuracies(wdbc,δ=0.3,X2)

图3 2 种邻域概率粗糙度(wdbc,δ=0.3,X1)Fig. 3 Two kinds of neighborhood probabilistic roughnesses(wdbc,δ=0.3,X1)

图4 2 种邻域概率粗糙度(wdbc,δ=0.3,X2)Fig. 4 Two kinds of neighborhood probabilistic roughnesses(wdbc,δ=0.3,X2)
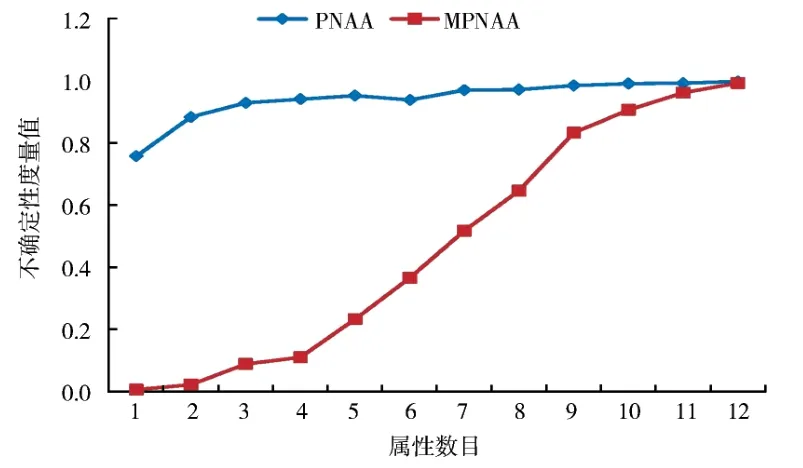
图5 2 种邻域概率近似精度(wdbc,δ=0.3,U/D)Fig. 5 Two kinds of neighborhood probabilistic approximation accuracies(wdbc,δ=0.3,U/D)
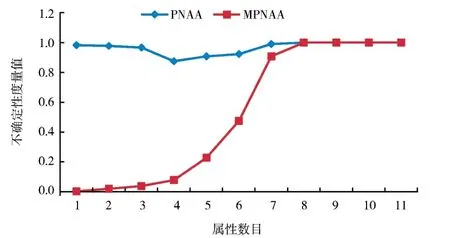
图6 2 种邻域概率近似精度(sonar,δ=0.05,U/D)Fig. 6 Two kinds of neighborhood probabilistic approximation accuracies(sonar,δ=0.05,U/D)
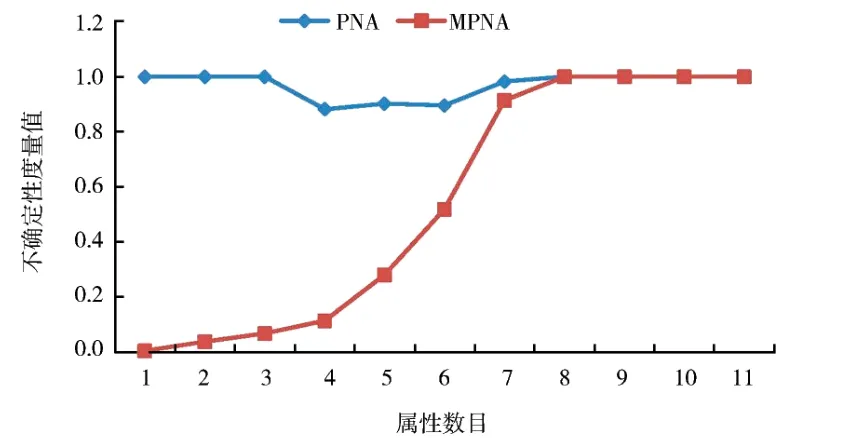
图7 2 种邻域概率精度(sonar,δ=0.05,X1)Fig. 7 Two kinds of neighborhood probabilistic accuracies(sonar,δ=0.05,X1)
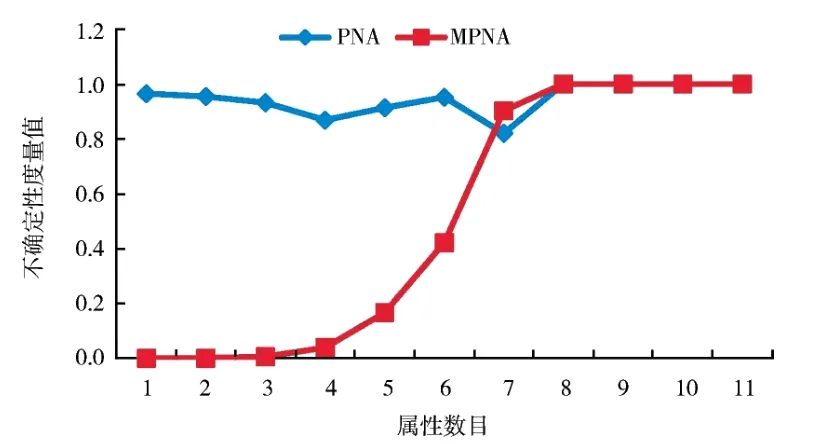
图8 2 种邻域概率精度(sonar,δ=0.05,X2)Fig. 8 Two kinds of neighborhood probabilistic accuracies(sonar,δ=0.05,X2)
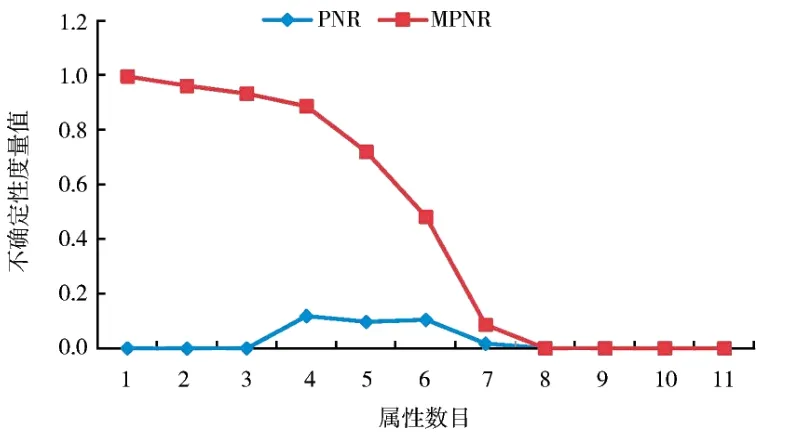
图9 2 种邻域概率粗糙度(sonar,δ=0.05,X1)Fig. 9 Two kinds of neighborhood probabilistic roughnesses(sonar,δ=0.05,X1)
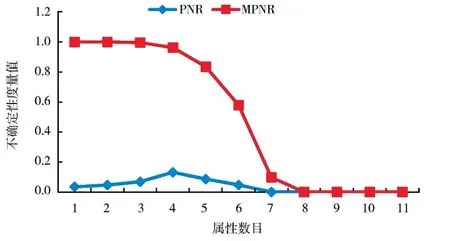
图10 2 种邻域概率粗糙度(sonar,δ=0.05,X2)Fig. 10 Two kinds of neighborhood probabilistic roughnesses(sonar,δ=0.05,X2)
在wdbc 和sonar 中,从图1、2 和图7、8 看出,随着属性的增加,邻域概率精度的值变化较平缓且具有非单调性,而改进的邻域概率精度变化明显且具有良好的单调性.而图3、4 和图9、10 显然体现出邻域概率粗糙度具有非单调性,而改进的邻域概率粗糙度具有单调性.图5、6 表明邻域概率近似精度具有非单调性,而改进的邻域概率近似精度具有明显的单调性.
4 结论
通过引入2 个阀值,提出邻域概率粗糙集模型,利用上下近似定义3 种不确定性度量,即邻域概率精度、粗糙度和近似精度;再将邻域概率粗糙集与邻域粗糙集相结合,提出3 种改进的不确定性度量,即改进的邻域概率精度、粗糙度和近似精度,并讨论其单调性.最后通过UCI数据实验对以上的不确定性度量的非单调性/单调性进行有效性说明.实验表明3 种改进的不确定性度量具有良好的单调性,为后期的属性约简研究奠定良好的基础.同时邻域概率粗糙集也是概率粗糙集[6]的推广.
致谢中国民用航空飞行学院面上项目(J2019-037)对本文给予了支助,谨致谢意.

