一类非自治分数阶随机反应扩散方程随机吸引子的分形维数

白欠欠， 舒 级， 李林妍， 李 辉

（四川师范大学 数学科学学院 可视化计算与虚拟现实四川省重点实验室，四川 成都610066）

0 引言

研究如下带加性噪声的非自治分数阶随机反应扩散方程

初边值条件为

其中，U⊆R3是具有光滑边界的有界区域，s∈（0，1），u=u（x，t）是定义在U×［τ，+∞）上的实值函数，τ∈R，W是概率空间（Ω，F，P）上的一维双边实值Wiener 过程，h∈D（（- Δ）s）∩W2s，p（U）（p≥4）.假设外力项g（x，t）与非线性项f（u）满足如下条件：

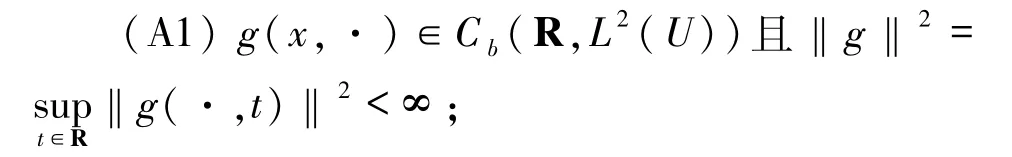
（A2）f（u）具有如下形式

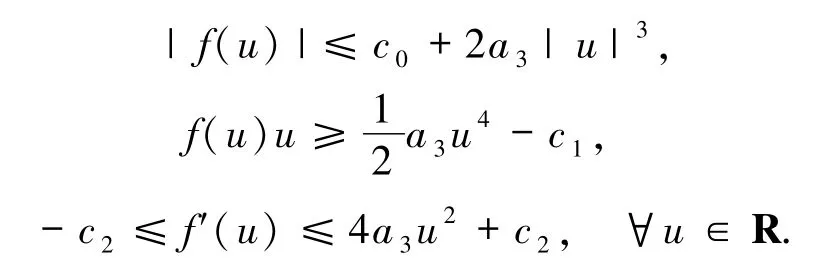
分数阶微分方程是指含有分数阶导数或者分数阶积分的一类方程，具有深刻的物理背景和丰富的理论基础.近年来，分数阶微分方程在物理学、生物学、化学及金融数学等许多领域得到广泛的应用，其中包括数学物理中的经典方程，比如分数阶Schrödinger方程［1-2］、分数阶Ginzburg -Landau 方程［3-8］、分数阶Landau - Lifshitz 方程［9］、分数阶Landau-Lifshitz-Maxwell方程［10］和分数阶反应扩散方程［11-12］.

当s∈（0，1）时，称（-Δ）s为分数阶拉普拉斯算子.在有界域U上，分数阶拉普拉斯算子有不同的定义，包括积分分数阶拉普拉斯算子和谱分数阶拉普拉斯算子2 种定义［13］.当s=1 时，（-Δ）s就是标准的拉普拉斯算子.文献［14 -19］提出拉回随机吸引子的概念，是确定系统整体吸引子［20-23］的推广，较好地刻画了随机动力系统的长时间行为.近年来，许多学者已深入研究带有标准拉普拉斯算子的随机方程的随机吸引子，比如自治方程［24-38］和非自治方程［12，39-45］.特别地，Zhou 等［45］对非自治随机反应扩散方程的随机吸引子的分形维数的上界进行了估计.对于分数阶随机反应扩散方程，目前仅有文献［11 -12，46］研究了随机吸引子的存在性，而随机吸引子的分形维数的有界性尚未有相关结论.受文献［12，45］的启发，本文研究方程（1）的随机吸引子的分形维数有界性.

1 预备知识

下面首先给出拉回随机吸引子和非自治随机动力系统的基本概念［11，33，42］.对于自治情形，可参见文献［16 -19］.

假设（X，‖·‖X）是一个可分Hilbert 空间，B（X）为X的Borel σ -代数，（Ω，F，P）是概率空间，（Ω，F，P，（θt）t∈R）是度量动力系统（MDS）.

定义1.1［33］映射Φ：R+×R ×Ω ×X→X称为X上关于（Ω，F，P，（θt）t∈R）的连续随机动力系统，若它对所有τ∈R，ω∈Ω及t，s∈R+，满足下列条件：

1）Φ（·，τ，·，·）：R+× Ω ×X→X是（B（R+）×F×B（X），B（X））-可测的；

2）Φ（0，τ，ω，·）=idX；

3）Φ（t+s，τ，ω，·）=Φ（t，τ+s，θsω，·）◦Φ（s，τ，ω，·）；

4）Φ（t，τ，ω，·）：X→X连续.

定义 1.2［42］1）X中的随机有界集｛B（ω）｝ω∈Ω称为关于（Ω，F，P，（θt）t∈R）是缓增的，若对P-a.e.ω∈Ω及∀b＞0，有

2）随机变量R（ω）称为关于（Ω，F，P，（θt）t∈R）是缓增的，若对P- a. e. ω∈Ω 及∀b＞0，有

定义1.3［33］D是X的所有随机子集的集合，K=｛K（τ，ω）：τ∈R，ω∈Ω｝∈D，则K称作Φ 的随机吸收集.如果对∀B∈D，存在TB（ω）＞0 使得对P-a.e.ω∈Ω，有

定义1.4［11］A=｛A（τ，ω）：τ∈R，ω∈Ω｝∈D，A称作是Φ 的一个D -拉回吸引子，如果满足下列条件：

1）对τ∈R，A（·，τ）：（Ω，F，P→2X是可测的，且A（τ，ω）在X中是紧的；

2）A是不变的，即对∀τ∈R，ω∈Ω，有Φ（t，τ，ω，A（τ，ω））=A（τ+ t，θtω），t≥0；

3）A吸引D的每个元素，即对B∈D，τ∈R，ω∈Ω，有

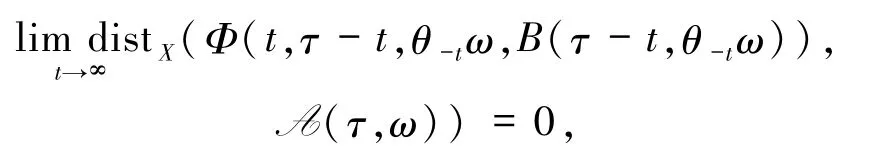
其中distX（·，·）表示X中2 个集合的Hausdorff半距离，即对2 个非空集合A，B⊆X，有

定义1.5［11］Φ称作是D-拉回渐近紧的，如果对∀τ∈R，ω∈Ω，D∈D，tn→∞，xn∈D（τ -tn，在X中有一个收敛子列.

定理1.6［33］Φ 是X上关于（Ω，F，P，（θt）t∈R）的连续Cocycle，若Φ 在X中有紧的随机吸收集，则Φ有唯一的D-拉回吸引子

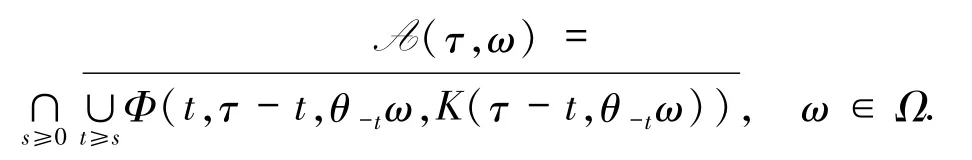
下面介绍分数阶导数及分数阶Sobolev 空间的相关知识［47］.

记S 是R3上的Schwartz空间，对0 ＜s＜1，u∈S，分数阶拉普拉斯算子（-Δ）s可以定义为

其中C（s）是与s有关的正常数，且

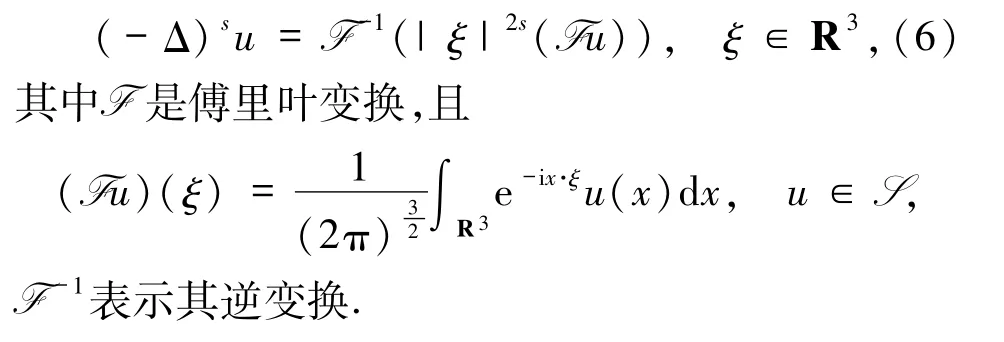
特别地，对∀u∈S，有为了方便起见，用‖·‖和（·，·）分别表示L2（R3）的 范 数 和 内 积，用‖· ‖p表 示Lp（R3）（p≥1）的范数，记Hs（R3）的Gagliardo 半范数为‖·‖˙H s（R3），有

引理1.7［48］若f，g∈H2s（R3），则有

其中s1与s2是非负常数，且s1+s1=s.

最后给出随机不变集的分形维数有界性定理.

定理1.8［45］设｛Φ（t，τ，ω）｝t≥0，τ∈R，ω∈Ω是可分Banach空间X上的一个随机动力系统，且度量动力系统（Ω，F，P，｛θtω｝t∈R）是遍历的.如果在X上存在有界闭的随机子集族｛X（τ，ω）｝τ∈R，ω∈Ω满足下述条件：对∀τ∈R，ω∈Ω，有以下几种情况：

（H1）存在缓增的随机变量Rω（独立于τ），使续的.

（H2）不变性：∀t≥0，X（t+τ，θtω）=Φ（t，τ，ω）X（τ，ω）.

（H3）存在正数λ、δ和t0，随机变量C0（ω）≥0，C1（ω）≥0，以及m维正交算子Pm：X→Pm X，（dim（PmX）=m）使得对∀τ ∈R，ω ∈Ω，u，v∈X（τ，ω），有：

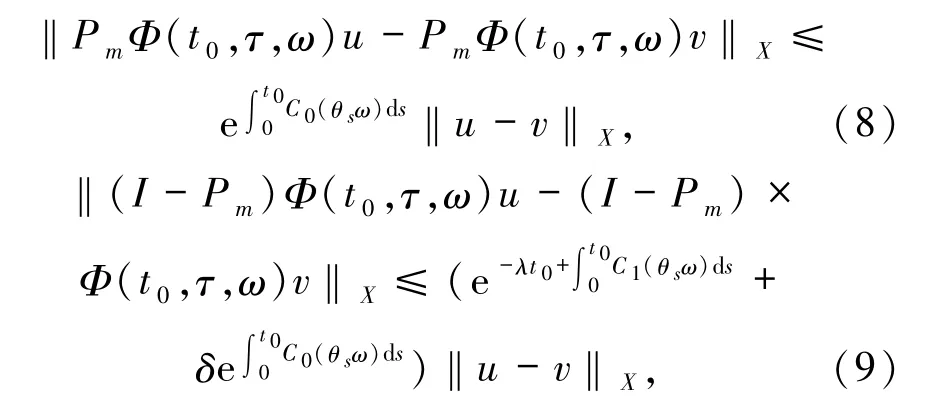
其中，λ、δ、t0、m独立于τ、ω.

（H4）λ、t0、δ、C0（ω）、C1（ω）满足

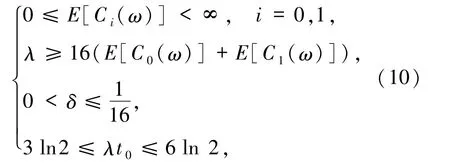
其中“E”表示期望，那么对于∀τ∈R，ω∈Ω，X（τ，ω）的分形维数有上界

其中Nε（X（τ，ω））表示在X中覆盖X（τ，ω），以ε ＞0 为半径的球的最小数量.

2 连续随机动力系统

方程（1）-（3）生成一个连续随机动力系统.

在概率空间（Ω，F，P）中定义时间平移算子θt：Ω→Ω，满足θtω（·）=ω（t+·）-ω（t），那么（Ω，F，P，（θt）t∈R）为一遍历度量动力系统.这里规定，对所有t∈R，ω∈Ω，W（t，ω）=W（t）（ω）=ω（t）.

设A=（-Δ）s是一个自伴且正定的线性算子，其特征值｛λi｝i∈N满足

下面将带加性白噪声的随机方程转化为只含有随机参数的方程.考虑一维Ornstein -Uhlenbeck过程

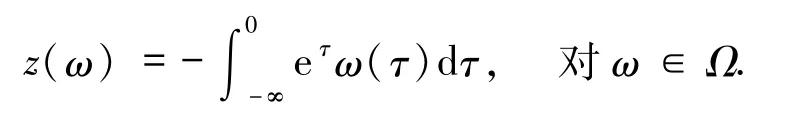
由文献［14，45］知，z（θtω）是随机方程dz+zdt=dW的平稳解，关于t连续，并且z（θtω）具有如下性质：

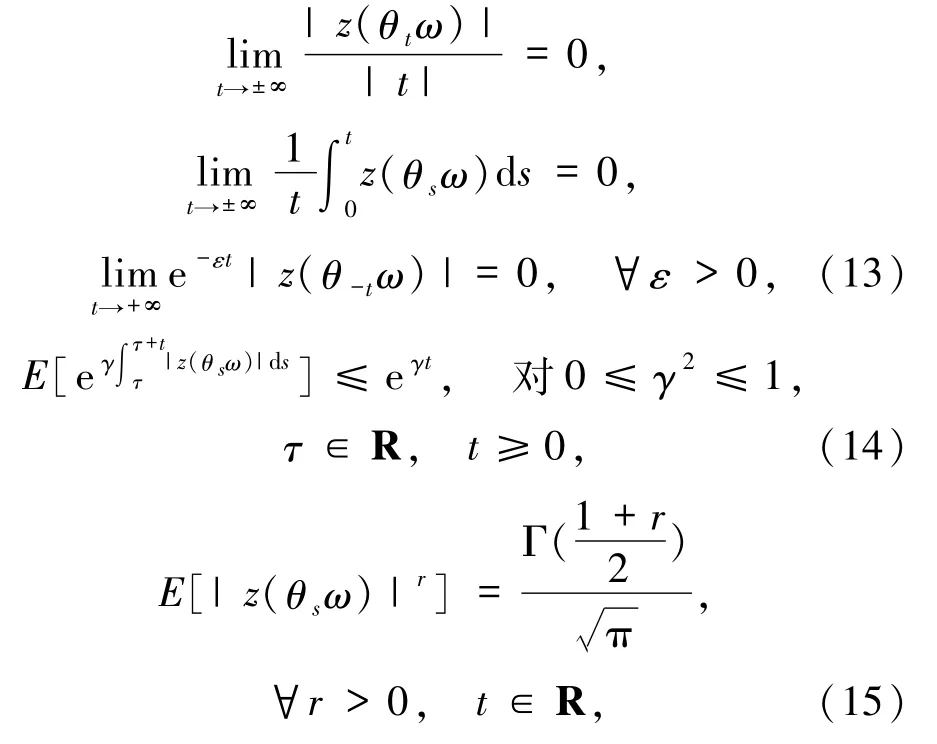
其中Γ是gamma函数.

令v=v（t，τ，ω，vτ）=u（t，τ，ω，uτ）-h（x）z（θtω），其中u（t，τ，ω，uτ）是方程（1）-（3）的解，uτ∈L2（U）是初始条件，那么方程（1）-（3）在L2（U）中等价于下述随机方程：

应用标准的Galerkin 方法，可以证明，在条件（A1）和（A2）下，对每一个ω ∈Ω，方程（16）在L2（U）中解是适定的［12］，从而可以在L2（U）上定义一个连续随机动力系统Φ：R+× R × Ω ×L2（U）→L2（U），有

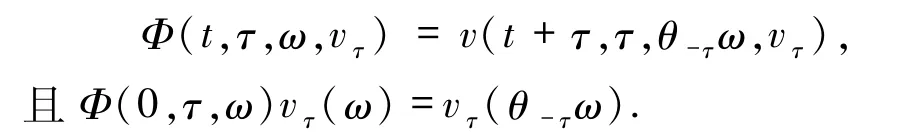
为了简便起见，字母ci（i=1，2，…）和kj（j=1，2，…）都表示正常数.

3 随机吸引子的存在性

设D是L2（U）中一些非空随机缓增子集构成的集族.为了证明随机吸引子的存在唯一性，首先给出Φ在L2（U）和Hs（U）中D -拉回吸收集的存在性.

引理3.1假设（A1）和（A2）成立，则对∀τ∈R，ω∈Ω，D=｛D（τ，ω）：τ∈R，ω∈Ω｝∈D，存在时间T0（τ，ω，D）≥0 以及一个缓增随机变量

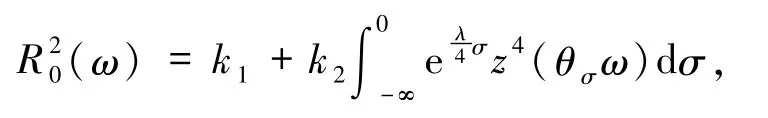
使得对∀t≥T0（τ，ω，D），方程（16）的解v（r，τ -t，ω，vτ-t）∈L2（U），vτ-t∈D（τ-t，θ-tω）满足

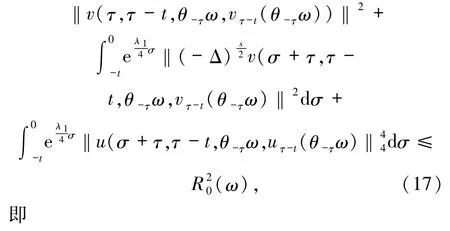
B0（ω）=｛v∈L2（U）：‖v‖≤R0（ω）｝是Φ在L2（U）中的D-拉回吸收集.

证明将方程（16）两边与v在L2（U）中作内积，得到

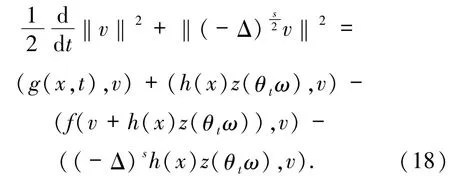
下面利用Young不等式、Hölder 不等式和条件（A2）估计（18）式中右边的每一项：

由Poincaré不等式以及h∈D（（-Δ）s）∩W2s，p（U）（p≥4），方程（18）变为

对（19）式在［τ -t，r］（r≥τ -t）上运用Gronwall引理，并用θ-τω替换ω，得到

由于vτ-t∈D（τ-t，θ-tω），且z（θtω）是缓增的.因此，当r= τ 时，由（20）式自然得到（17）式，且R0（ω）是一个缓增的随机变量.

引理3.2假设（A1）和（A2）成立，则对∀τ∈R，ω∈Ω，D=｛D（τ，ω）：τ∈R，ω∈Ω｝∈D，存在时间T1（τ，ω，D）≥1 以及2 个缓增随机变量：

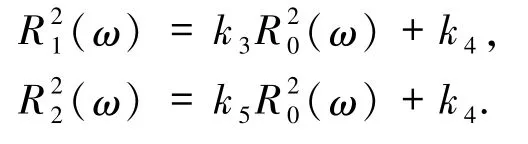
使得（16）式的解v（r，τ -t，ω，vτ-t）∈L2（U），vτ-t∈D（τ-t，θ-tω）满足：

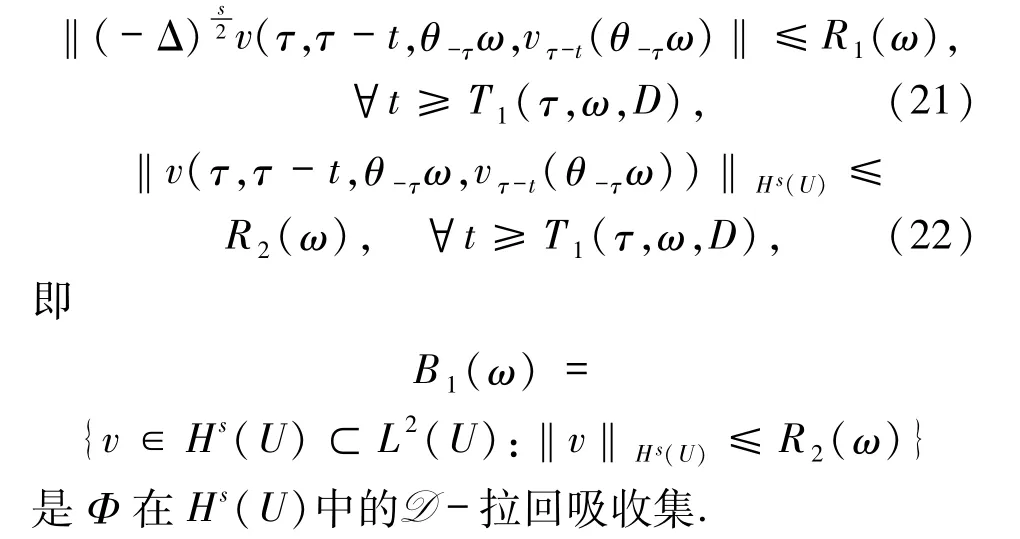
证明将（16）式两边与（-Δ）sv在L2（U）中作内积.并由

对（24）式关于σ在［τ-1，τ］上再次积分，得到

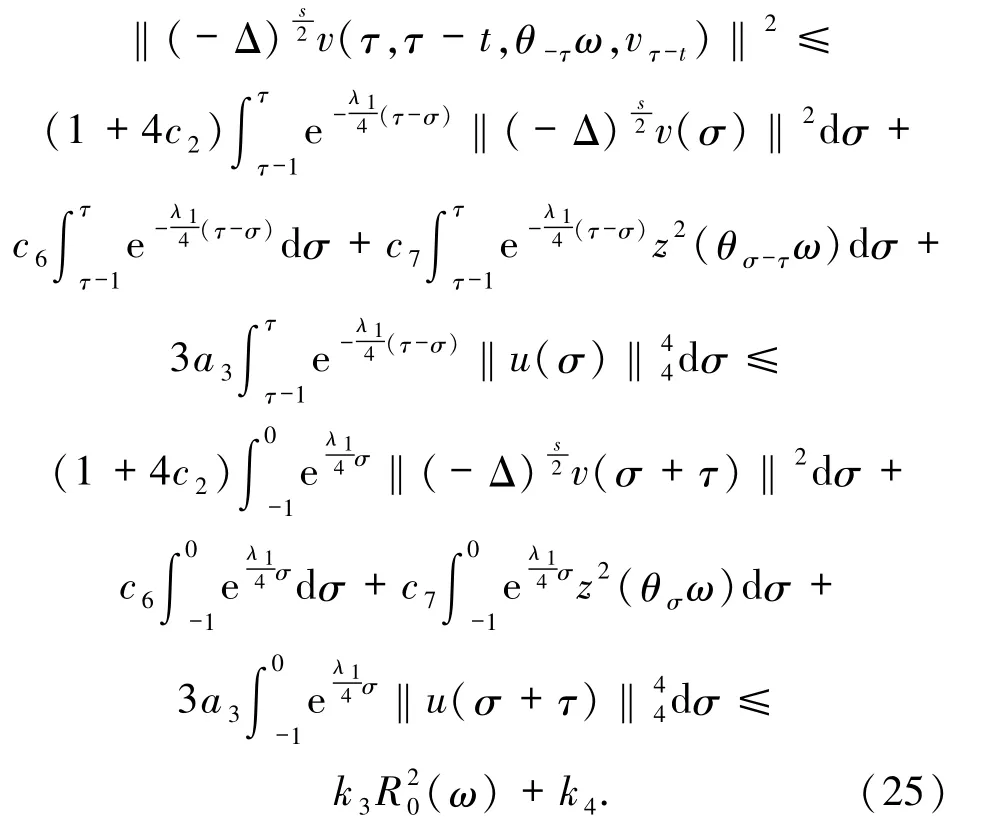
由（17）式与（25）式知（21）式成立.

现在由引理3.1 与引理3.2 可得Φ 在L2（U）上的随机吸引子的存在唯一性.

定理3.3假设（A1）和（A2）成立，则随机动力系统Φ在L2（U）上存在唯一的D -拉回吸引子A=｛A（τ，ω）：τ∈R，ω∈Ω｝∈D，并满足

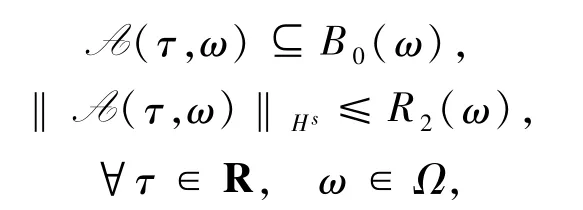
其中R2（ω）同上.

证明对∀τ∈R，ω∈Ω，由引理3.1、引理3.2及紧嵌入可知，B1（ω）是Φ 在L2（U）中的一个紧可测D-拉回吸收集.因此，由定理1.6，Φ在L2（U）上生成一个唯一的D -拉回吸引子A=｛A（τ，ω）：τ∈R，ω∈Ω｝∈D，且对∀τ∈R，ω∈Ω，A（τ，ω）⊆B0（τ，ω）∩B1（τ，ω）.

4 随机吸引子的分形维数

利用定理1.8 估计Φ 的随机吸引子A（τ，ω）的分形维数上界.

显然，A（τ，ω）满足定理1.8 的（H1）和（H2）.下面证明A（τ，ω）的Lipschitz 性质.对于∀τ∈R，ω∈Ω，vjτ（ω）∈A（τ，ω），j=1，2，令

由A（τ，ω）的不变性、Φ 的Cocycle 性质以及定理3.3 知，对于r≥τ，v1（r），v2（r）∈A（τ，θrω）⊆B1（θr（ω）），且

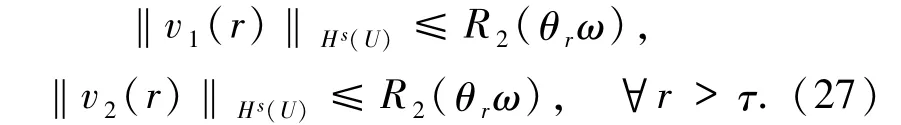
引理4.1假设（A2）成立，则对∀τ∈R，ω∈Ω，t≥0 以及vjτ（ω）∈A（τ，ω），j=1，2，有

证明将（26）式与y（r）在L2（U）中作内积，并由

对（29）式在［τ，τ +t］上运用Gronwall 引理，并用θ-τω替换ω，可得（28）式.

下面证明A（τ，ω）满足（H3）.令｛ei｝i∈N为算子A的特征值｛λi｝i∈N相对应的特征函数，即满足Aei=λiei，则｛ei｝i∈N构成L2（U）的一组标准正交基，记

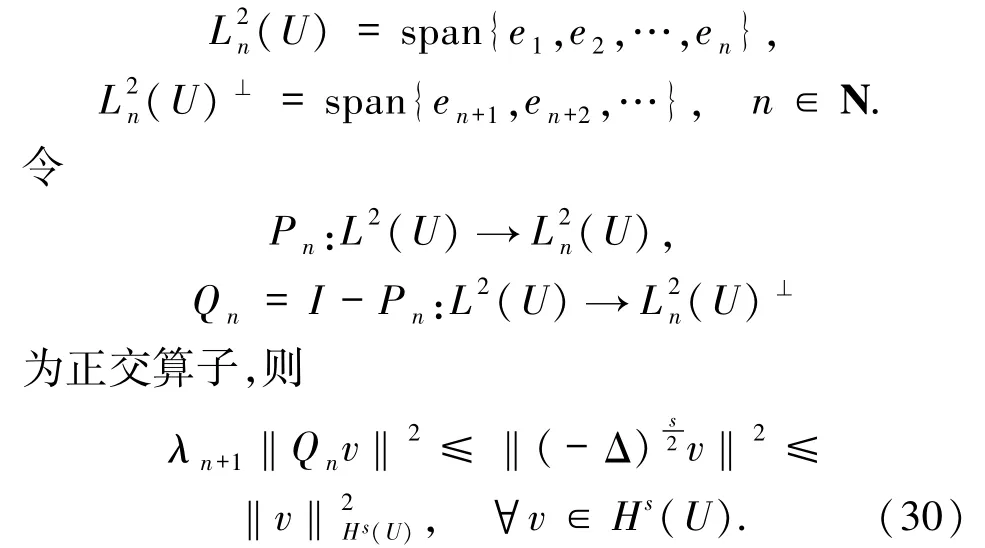
引理4.2假设（A1）和（A2）成立，则对∀τ∈R，ω∈Ω，t≥1，存在一个随机变量M0（ω）≥0 及一个n维正交算子Pn：L2（U）→L2n（U），使得对∀vjτ（ω）∈A（τ，ω），j=1，2，有：

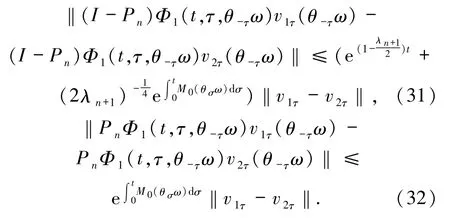
证明将（26）式与yn=Qny在L2（U）中作内积，则

利用Hölder 不等式和Young 不等式，并结合条件（A2）与（27）式有

其中ϑ∈（0，1）.结合（33）和（34）式得到

对（35）式在［τ，τ+t］（t≥0）上运用Gronwall引理，并用θ-τω替换ω，可得

由（28）式与M0（ω）＞c2≥0 知（32）式成立.

引理4.3对∀τ∈R，ω∈Ω有

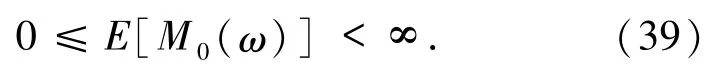
证明首先，gamma函数Γ有如下性质：

下面证明M0（ω）的每一项的期望有界.由引理3.1 与引理3.2 得：

再由（15）与（40）式可得

因此，由（41）和（42）式知

进一步，由（38）式可得

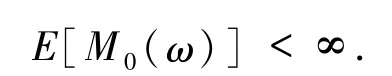
根据定理1.8、引理4.2 和引理4.3，可得到这一节的主要结论.

定理4.4假设（A1）和（A2）成立，则对∀τ∈R，ω∈Ω，A（τ，ω）的分形维数有上界再由（12）和（39）式知，存在有限整数n0∈N使得

令（31）与（32）式中t=t0＞0 满足