材料中带有记忆项的随机热方程在薄域上的随机吸引子

李 辉， 舒 级， 白欠欠， 李林妍

（四川师范大学 数学科学学院 可视化计算与虚拟现实四川省重点实验室，四川 成都610066）

近年来，许多学者从不同的角度对薄域问题进行了广泛的讨论，用渐近展开、奇异摄动等方法研究了这类问题.确定耗散系统在薄域上的渐近行为的系统研究首先由Hale等［1］提出.后来他们的结果被大量引用［2］.除此之外，Chueshov 等［3］研究了薄域T2×（0，ε）上随机3D Navier -Stokes 方程的遍历性，其中T2为一个二维环面.Caraballo等［4］研究了一类半线性抛物型随机方程组在薄有界管状域内的同步问题.

设Q是Rn（n≥1）上光滑有界区域，Oε是如下定义的n+1 维区域：

其中g∈C2（¯Q，（0，+∞）），0 ＜ε≤1.易知存在正数r1、r2，使得对∀x*∈¯Q，有

本文考虑薄域Oε上加性噪声驱动的带有记忆项的随机热方程

初值为

其中τ∈R，λ0，β ＞0，γ 是一个非负递减的记忆核，是定义在˜O ×R上的非负函数，h（x）∈C2（¯Q ×［0，r2］），W是定义在概率空间上的双边实值Wiener 过程.s）Δ＾uε（s）ds是与＾uε有关的依赖过去历史的扩散项.

众所周知，方程（2）来源于带记忆项的热流理论［5］，它描述了一个依赖于温度的反应过程.当γ=0，方程（2）不含记忆项，方程（2）简化为带噪声的随机抛物方程.在这种情况下，文献［6 -7］中证明了随机反应扩散方程的遍历性和随机吸引子的存在性.当不含噪声时，方程（2）在文献［8］中进行了一些讨论.

由于随机偏微分方程开始出现在各种各样的应用中，需要考虑一些不确定性因素或随机影响，它们被称为噪声.全局随机吸引子的研究可以追溯到Ruelle的结果［9］.随机系统的拉回吸引子的概念首先被文献［10］引入，推广了文献［11］中确定性方程的全局吸引子.随机偏微分方程的随机吸引子已被许多学者讨论，比如自治随机方程［12-17］、非自治随机方程［18-22］.最近，文献［5］得到了一些关于带有记忆项的随机方程的随机吸引子的结果.另外，文献［23］证明了薄域上随机反应扩散方程的随机吸引子的存在性.然而在薄域上带有记忆项的随机方程却很少有结果.受文献［23 -24］的启发，在本文中将研究方程（2）（3）的随机拉回吸引子的存在性.为了在薄域Oε上处理方程（2）（3），需要转换方程（2）（3）到一个固定区域O上.另一方面，由于记忆项包含了现象过去的全部历史，无法证明其随机动力系统的紧性，但是它的渐近紧性可以通过分解方法［8］来证明.

1 随机动力系统

本节给出问题（2）（3）解的存在性和唯一性，并且该解在薄域Oε上能生成一个连续随机动力系统.考虑如下方程

初值为

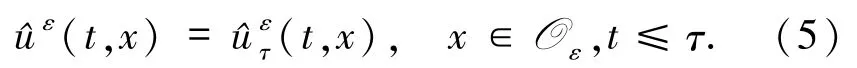
假设f满足如下条件：对所有x∈˜Q，＾uε∈R，

下面将方程（1）（2）转化为区域O上的有界边值问题.对∀x=（x*，xn+1）∈Oε，定义变换：

对于上述薄域空间，引入新的函数空间并定义相关的內积与范数.首先赋予空间Hg（O）內积

现在考虑概率空间（Ω，F，P），其中Ω =｛ω∈C（R，R）：ω（0）=0｝，F 是由Ω 的紧开拓扑导出的Borel σ-代数，P是（Ω，F）上对应的Wiener 测度.这里规定W（t，ω）= ω（t），t∈R.定义时间平移算子

那么（Ω，F，P，｛θt｝t∈R）是一个度量动力系统.

给定ω∈Ω，令

2 解的一致估计

ω、ε、B无关的正常数.

证明将（28）式与vε在空间Hg（O）中做内积，有

引理2.2假设（6）-（12）式成立，则存在ε0＞0，对∀0 ＜ε ＜ε0，ω∈Ω，τ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在与ε 无关的T=T（τ，ω，B）＞1，使得对∀t≥T，方程（28）-（31）的解满足

由（8）和（9）式可得

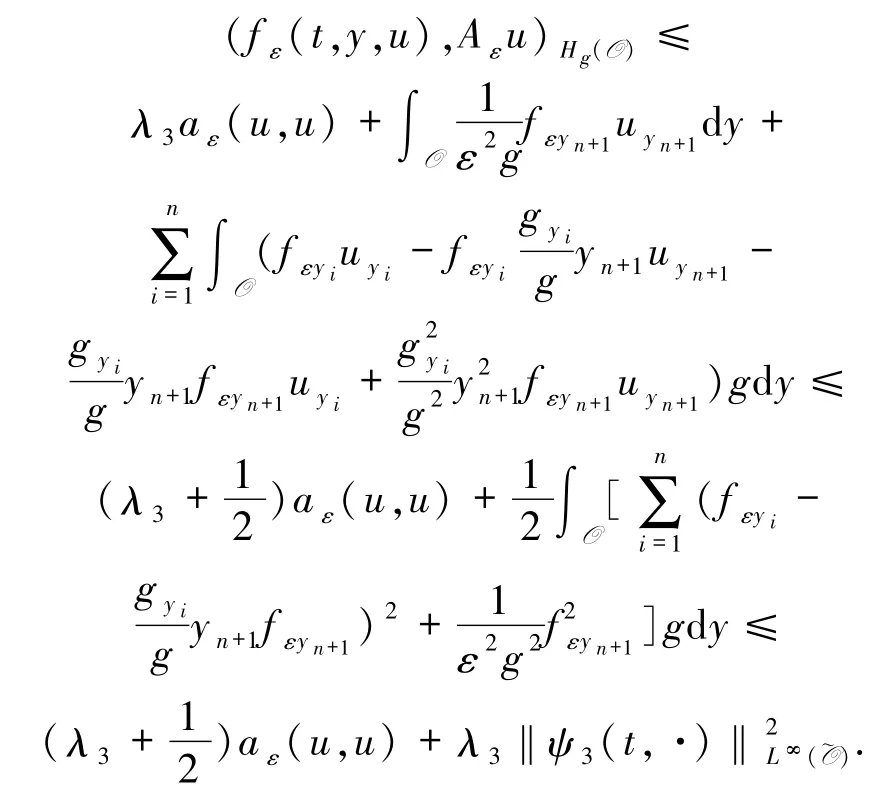
从而结论得证.

3 渐近紧性

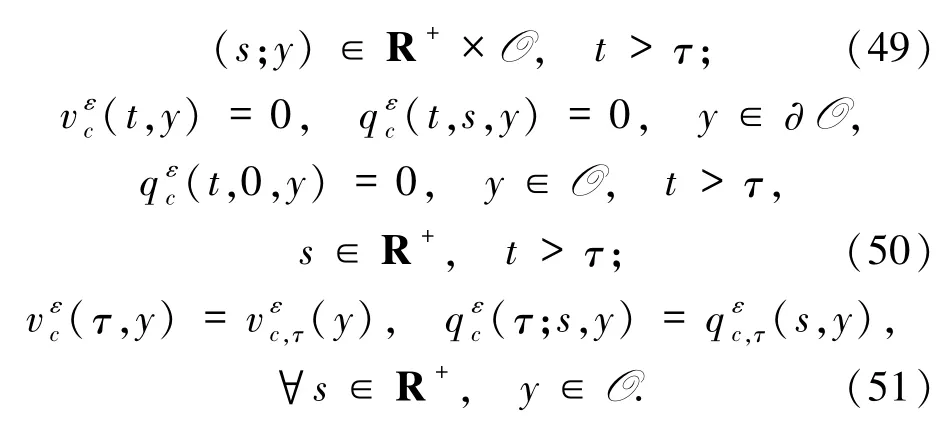
显然，问题（44）-（47）和（48）-（51）的适定性可由Galerkin方法得到.

类似引理2.1 得

引理3.1假设（6）-（11）和（32）式成立，则存在ε0＞0，对∀0 ＜ε ＜ε0，ω ∈Ω，τ ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在与ε 无关的T=T（τ，ω，B）＞0，使得对∀t≥T，方程（44）-（47）的解满足

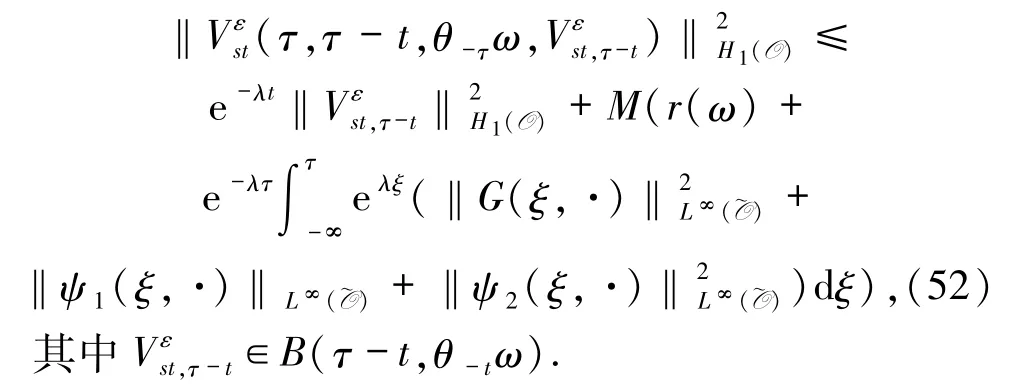
由引理3.1 易得：

引理3.2假设（6）-（11）和（32）式成立，则存在ε0＞0，对∀0 ＜ε ＜ε0，ω ∈Ω，τ ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在与ε 无关的T=T（τ，ω，B）＞0，使得对∀t≥T，方程（48）-（51）的解满足

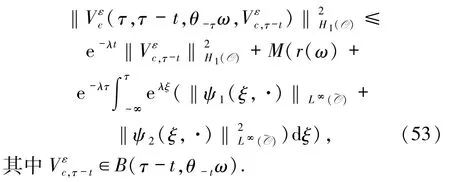
引理3.3假设（6）-（12）式成立，则存在ε0＞0，对∀0 ＜ε ＜ε0，ω∈Ω，τ∈R，B=｛B（τ，ω）：ω∈Ω，τ∈R｝∈D，存在与ε无关的T=T（τ，ω，B）＞1，使得对∀t≥T，方程（48）-（51）的解满足

证明将（8）式与在空间Hg（O）中做內积，有

由（49）、（10）和（11）式得：

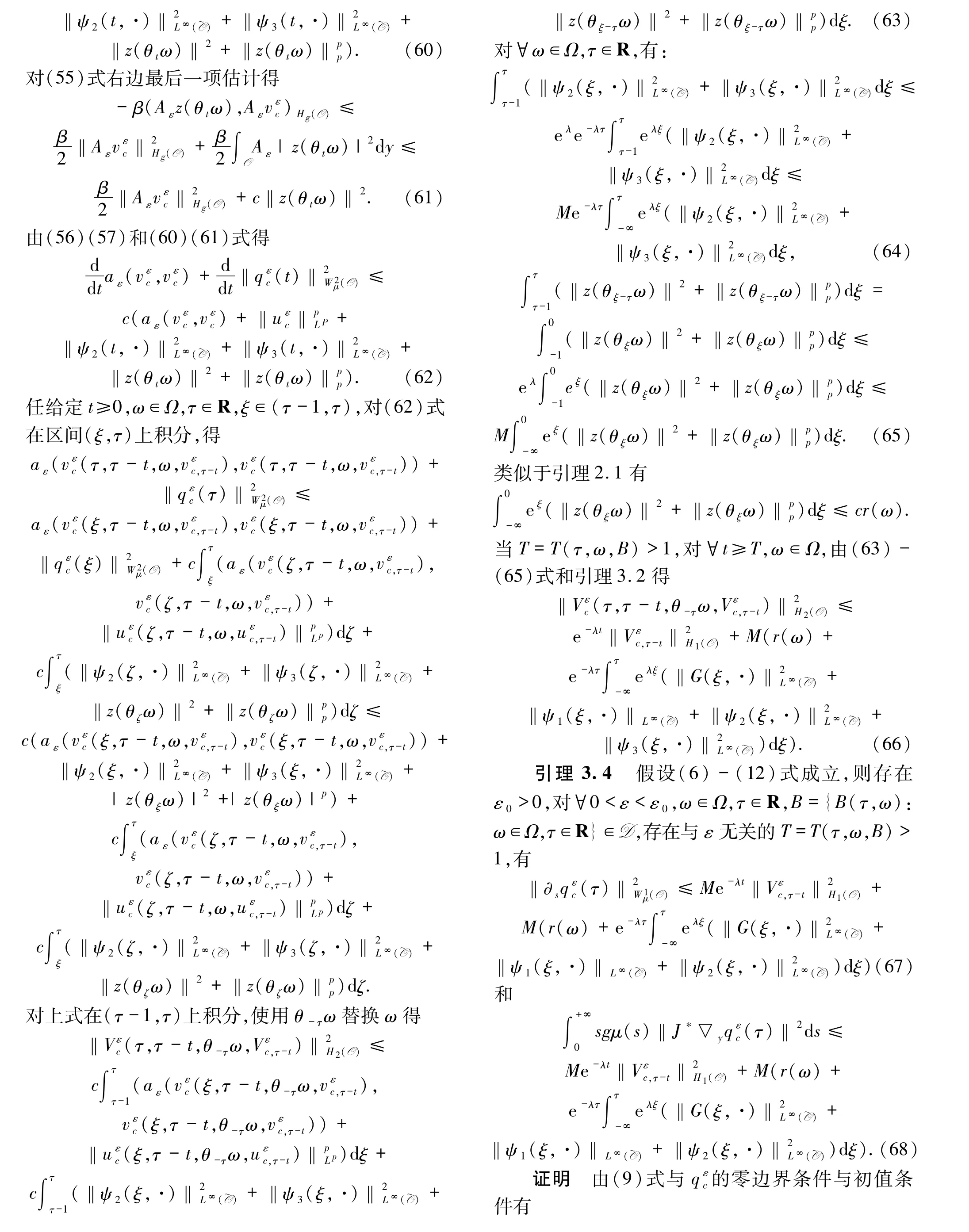
4 拉回吸引子的存在性

本节给出随机方程（28）-（31）式对应的cocycle Φε的D1-拉回吸引子的存在性.

定理4.1假设（6）-（11）和（32）（33）式成立，则存在ε0＞0，对∀0 ＜ε ＜ε0，cocycle Φε在空间H1（O）中存在唯一D1-拉回吸引子Aε=｛Aε（τ，ω）：ω∈Ω，τ∈R｝∈D1.

证明由引理3.5 和3.6、问题（28）-（31）生成的随机动力系统在D1中是渐近紧的.因此，Φε存在唯一D1-拉回吸引子.

致谢可视化计算与虚拟现实四川省重点实验室对本文给予了资助，谨致谢意.