不定二次型的判定方法及其应用

付宏伟，曾梅兰①

（湖北工程学院 数学与统计学院，湖北 孝感432000）

0 引言

二次型正定性的理论在数学和物理的许多分支中有着广泛的应用［1-4］. 到目前为止，关于二次型的正定、半正定、负定、半负定的判定问题已有很多结果［5-9］，关于不定二次型的判定问题讨论却较少. 文献［10］给出不定二次型的判定及其分类. 本文给出不定二次型的性质、判定定理及其应用.

定义［11-12］对于实二次型f(x1，x2，…，xn)=XTAX，其中矩阵A是实对称的. 如果存在实向量同时存在实向量X2=(b1，b2，…，bn)T≠0 ，使 得则称矩阵A为不定矩阵，该二次型为不定二次型.

1 主要结果

下面给出不定二次型的性质与判定定理.

性质设实二次型是不定二次型，则存 在(c1，c2，…，cn)≠0 ，使 得

f(c1，c2，…，cn)=0.

证明由于f(x1，x2，…，xn)=XTAX是实二次型，则存在可逆的线性替换X=CY，使得

这里p,q为非负整数，且p+q≤n. 又f(x1，x2，…，xn)为不定二次型，那么存在实向量X1=(ɑ1，ɑ2，…，ɑn)T≠0，使得f(X1)=X1TAX1＞0，因此，p≥1. 同时存在实向量X2=(b1，b2，…，bn)T≠0，使得f(X2)=XT2AX2＜0 ，那 么，q≥1. 令Y3=εp+εp+1,X3=CY3=(c1,c2,…,cn)T，其 中εi=(0,…,1,…0) ，则X3≠0，且f(c1，c2，…，cn)=1-1=0.

定理对于实二次型f(x1，x2，…，xn)=XTAX，其中矩阵A是实对称的，则下列条件等价：

（1）f(x1，x2，…，xn)是不定二次型；

（2）在实可逆矩阵C，使得其中p,q均为正整数，且p+q≤n；

（3）A 既有正特征值，又有负特征值.

这里λ1，λ2，…，λn是A 的全部特征值. 作正交变换X=CY ，则f(x1，x2，…，xn)=λ1y21+λ2y22+…+λny2n. 由于f(x1，x2，…，xn) 为不定二次型，那么存在实向量X1=(ɑ1，ɑ2，…，ɑn)T≠0 ，使得f(X1)＞0 ，因此，存在λi＞0. 同时存在实向量X2=(b1，b2，…，bn)T≠0，使得f(X2)＜0，那么，λj＜0. 故A 既有正特征值，又有负特征值.

(3)⇒(1) 设A 有p 个正特征值λ1，…，λp，q 个负特征值-λp+1，…，-λp+q，则存在正交矩阵C，使得

作正交变换X=CY ，则

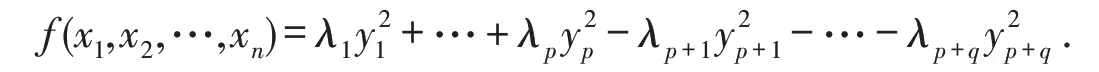
令X1=Cε1，则f(X1)=λ1＞0. 令X2=Cεp+1，则f(X2)=-λp+1＜0. 故f(x1，x2，…，xn)是不定二次型.

2 应用举例

从不定二次型的定义和判定定理，得到不定二次型的3种判定方法：定义法、合同法和特征值法. 有些不定二次型的判定较为复杂，如何灵活运用这几种判定方法，下面给出其应用举例.

证法1（定义法） 设λ 是A 的特征值，由于A 可逆，则λ ≠0 且存在向量x ≠0，使得

那么，

证法2（合同法）A可逆，则存在可逆矩阵P,Q，使得PAQ=E，那么