偏最小二乘回归分析在空气质量监测数据校准中的应用
李艳午,王佳欢①
(芜湖职业技术学院,安徽 芜湖241003)
0 引言
多元回归分析是研究多变量相关性的统计分析方法,在生物统计学、社会科学、行为科学、气象预报等领域有着广泛的应用[1].
多元回归分析的方法有很多,聚类分析、主成分分析、典型相关性分析、偏最小二乘回归分析等都是多元回归分析的代表性方法. 其中,偏最小二乘回归分析是一种通过使误差的平方和最小化,找到数据的最佳匹配函数的回归模型. 这种模型提供一种多对多线性回归建模的方法,特别是当两组变量的个数较多且存在多重相关性时,用此方法建立的回归模型[2-6],具有传统的经典回归分析方法所不具有的优点.
1 空气质量监测数据校准的偏最小二乘回归分析模型
1.1 问题的提出
随着工业化和城市化的高速发展,环境污染已经成为社会发展和科技进步的沉重代价. 尤其是大量化石燃料的使用、工农业生产的排放、居民生活垃圾的焚烧等带来的大气污染,日益成为危害人民健康、破坏自然环境的罪魁祸首. 所以,大气污染防治成为世界各国共同关注的一个社会问题,也引起学界研究[7-10].
空气质量的有效监测是做好大气污染防治的基础性工作. 目前,对空气质量的监测通常是通过对“两尘四气”(PM2.5、PM10、CO、NO2、SO2、O3)浓度的监测来实现的. 通常在一个城市会选择若干个监测点作为国家监测控制站点(简称为国控点),每隔一定时间(如:1 h)发布一次相关的监测数据,这些数据能较为准确地反映监测点附近的空气质量状况. 但是,由于国控点的布控较少、数据发布时间滞后(时间间隔通常在1 h以上)、花费较大等原因,无法实时给出空气质量的监测和预报.
现有一种便携式微型空气质量监测仪,可以对某一地区空气质量进行实时网格化监控,并能同时监测温度、湿度、气压、风速、降水等气象参数. 但是,由于这种检测仪所使用的电化学气体传感器在长时间使用后,会产生一定的零点漂移和量程漂移,非常规气态污染物和天气因素也都会对传感器产生影响,这就会使得在同一时间内微型空气质量监测仪所监测的数据与该国控点的数据产生一定的差异. 因此,需要利用国控点的数据对临近点用这种微型监测仪监测的数据进行校准,以提高监测数据的精度.
影响微型监测仪监测数据的因素主要有2大类:空气质量(6个指标)和气象因素(5个指标),这2类因素又相互交叉影响. 因此,这是典型的多变量相关性分析问题,适宜用偏最小二乘回归分析来建模.
1.2 偏最小二乘回归分析模型
首先,设置变量:用x1,x2,…,x6分别表示国控点的指标PM2.5、PM10、CO、NO2、SO2、O3的数据;用x7,x8,…,x11分别表示自行监测点的温度、湿度、风速、气压、降水等气象指标的数据;用zj,j=1,2,…,6 分别表示自建点6项空气质量指标校准值. 用i1,i2,…,im分别表示监测数据发布的第1个、第2个、…、第m个时间点,第i个时间点x1,x2,…,x11的监测值分别记作[ɑi1,ɑi2,…,ɑi,11],监测数据矩阵A=(ɑij)m×11.
建模的步骤如下:
第1步数据标准化
将自变量的指标值ɑij转化为标准化指标值ɑ˜ij.

为对应的标准化变量.
第2步求相关系数矩阵
利用MATLAB软件,可以计算出6个因变量加11个自变量的相关系数矩阵R17×17.第3步分别提出自变量组和因变量组的成分
利用Matlab软件,求得各对成分分别为:

第4步求回归方程
在具体数据下,如果前p个成分解释自变量的比率达90%以上,那么只要取p对成分即可求得自变量组和因变量组与u1,u2,…,u6之间的回归方程,分别如下:
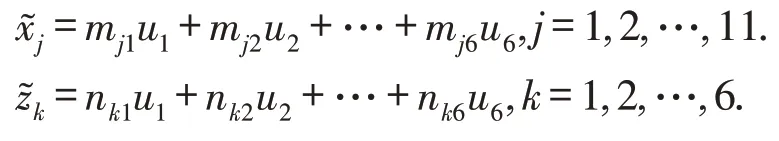
第5步求因变量组与自变量组之间的回归方程
把第3步中的ui代入第4步中的回归方程,得到标准化指标变量之间的回归方程:

再将标准化变量˜˜(i=1,2,…,6;j=1,2,…,11)分别还原成原始变量zi,xj,即得到回归方程:

2 模型仿真与误差分析
2.1 模型的仿真检验
利用2019年全国大学生数学建模竞赛D题所提供的原始数[11],作仿真与误差分析. 首先,对原始数据做了预处理,剔除有问题的数据,最值保留189 d的数据;并对保留数据做了平滑处理,即把两组数据都转化为每天的均值.
然后,对平滑处理后的自建点和国控点数据作相关性分析和误差分析. 相关性分析的结果表明,2个监测点的PM2.5指标相关性程度较高,达到显著相关的程度,PM10的相关性程度也较高,而其他4种气体的相关性程度则较低. 这表明该仪器监测的实时数据中PM2.5和PM10的可信度较高,对空气质量的监测数据有一定可信度和参考价值. 误差分析的结果表明,监测指标PM2.5的相对误差较小,而NO2的相对误差较大,6项指标相对误差综合排序为:

这表明便携式监测仪的监测数据非常有校准的必要.
为探索便携式监测仪数据产生误差的因素,分析影响自建点6项空气指标的因素及强弱排序. 从影响因素的排序结果可见,PM2.5 和PM10 是影响各个监测指标的2 个主要因素,而气象因素则是次要因素.
最后,按照偏最小二乘回归分析的建模步骤,建立自建点的6个空气质量指标变量与国控点的6个空气质量指标变量和5个气象指标变量之间的回归方程为:

从校准数据的拟合预测图来看,PM2.5、PM10 拟合效果是比较理想的,CO、NO2、O3的拟合效果也不错,只有SO2一个指标拟合的效果不够理想.

图1 校准后的数据预测图
2.2 误差分析
把自建点的11项指标数据代入回归方程,即可得到校准后的数据,为直观地量化评价模型的精度,把校准后的数据与国控点的数据再作总体的相对误差分析,结果如表1.

表1 自建点相对于国控点的数据的总体相对误差
结果表明,6项监测指标中除SO2外其余监测指标校准后的数据总体相对误差均有明显下降,这说明所建立的回归方程可以很好地对便携式监测仪的监测数据进行有效地校准.
3 结语
偏最小二乘回归分析与主成分分析法,虽然都是对主成分进行回归,但是在解决多元线性回归中的多变量多重相关性问题时,两者还是有一些不同之处的. 主成分分析只利用自变量的信息,而偏最小二乘回归分析运用自变量和因变量的信息,所以回归的效果比主成分分析要好.
基于变量之间的多重相关性,建立的偏最小二乘回归分析模型,集中主成分分析、典型相关性分析和线性回归分析法的特征,不仅提供一个合理的回归模型,而且完成一些类似于主成分分析和典型相关性分析的研究内容,得到一些有意义的结果.
便携式空气质量监测仪监测数据误差影响因素的多重性与交互性,契合偏最小二乘回归分析的问题背景和数学思想. 利用偏最小二乘回归分析理论,建立的监测数据校准模型在一定程度上提高监测数据的精度,对空气质量的监测有实际意义.
事实上,造成空气质量监测数据产生误差的多重因素及交互影响,具有神经网络模型的背景[14-15]. 所以,可以考虑建立神经网络模型对便携式空气质量监测仪的数据进行校准,这是本文研究进一步完善和改进的一个方向.

