Lowner微分方程与调和拟共形映射
聂云梦,黄华鹰①
(安徽大学 数学科学学院,安徽 合肥230601)
0 引言

设F(ω,t)∈C2(D,[0,T]),D表示复平面C上的单连通区域,t∈[0,T],T >0,对Lowner微分方程1990年,Reich在文献[1]中证明以et-拟共形映射ω=f(z,t)为解的Lowner微分方程式(1)中复值连续函数F(ω,t)满足,同时证明若F(ω,t)是定义在Δ×[0,T]上的拟共形形变,且存在非负常数A,满足|Fωˉ(ω,t)|≤A,则Lowner 微分方程式(1)存在拟共形映射解. 2011 年,魏华影[2]推广Reich 的结果,证明如果F(ω,t)是定义在Δ×[0,T]上的拟共形形变,且存在非负连续函数A(t),满足|Fωˉ(ω,t)|≤A(t),则方程(1)的解是-拟共形映射,进一步证明了解ω=f(x,t)是R→R的拟对称同胚,当且仅当F(ω,t)满足

对任意的ω∈R,h>0 成立,其中R是实轴,F(t)是关于t的非负连续函数. 并且对于单位圆周Γ上的情形,文献[2]也给出类似的结果. 对于Lowner微分方程(1)在拟共形映射和拟对称同胚的参数表示中的具体研究可参考文献[3-9]等.
本文将考虑一类特殊的拟共形映射—调和拟共形映射. 1968 年,Martio[10]提出这一类函数,随后,Partyka和Sakanf分别在文献[11-12]中给出关于调和拟共形映射的更多例子和性质. 特别地,Kalaj等[13]给出任一上半平面H上的调和拟共形映射f(z),其中z=x+iy∈H,具有唯一的表示形式:

其中:u(x,y)为实值调和函数,c为固定常数.
本文将结合这一类调和拟共形映射与Lowner微分方程,考虑以下问题:具有一族上半平面的调和同胚(或调和拟共形映射)解的Lowner微分方程,F(ω,t)满足什么条件?
本文主要给出2个定理.
1 预备知识
首先给出一些基本概念.
定义1.1[14]设f(z)=u(x,y)+iv(x,y) 是平面区域D⊂C内具有二阶连续偏导函数的复值函数,即f(z)∈C2(D),z=x+iy∈D, 若f(z)的拉普拉斯算子
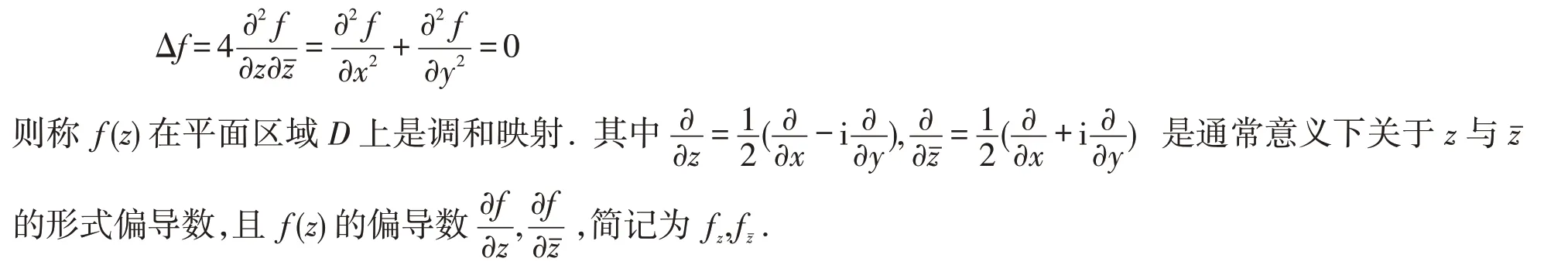
设f(z)是平面单连通区域D上的调和映射,则f(z)具有如下形式

其中g(z),h(z)是平面区域D内的全纯函数,且其幂级数形式可以写成
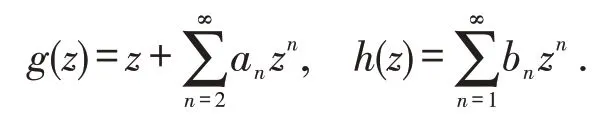
关于调和映射的表示形式可参考文献[14].
由Lewy 定理可知,函数f(z) 在平面区域D上局部单叶当且仅当f(z) 的Jacobian 行列式Jf=|fz|2-|fzˉ|2≠0.
若Jf >0,则称f(z)是区域D上的保向映射.
如果g(z),h(z)是平面区域D内的全纯函数,则关于z的偏导数gz(z),hz(z)可写成g′(z),h′(z).
定义1.2[15]复值连续函数F∈C2(D)在平面区域D内有广义偏导数Fzˉ,且Fzˉ∈L∞(D),则称F是区域D内的拟共形形变. 其中L∞(D)是指在平面区域D上本性有界函数全体.
拟共形映射定义有多种形式,本文利用以下分析定义.
定义1.3[16]设f(z):D→D′是区域D到区域D′的保向同胚,若f(z)在区域D内线段上几乎处处绝对连续,且存在常数K≥1,使得不等式
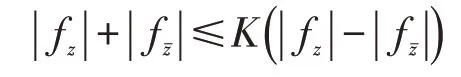
对几乎处处z∈D都成立,则称f(z)是K-拟共形映射. 特别地,当K=1时,f(z)为共形映射.
由拟共形映射的分析定义可知,K-拟共形映射ω=f(z)满足如下的Beltrami方程

2004年,Duren[14]证明,若ω=f(z)是平面区域D内具有二阶偏导数的同胚映射,则f是调和函数当且仅当f的第二复伸张νf在区域D内是全纯函数.
2 主要结果
首先给出存在调和同胚解的Lowner方程所需的必要条件.
定理2.1设F(ω,t)∈C2(H,[0,T]),若Lowner 微分方程(1)的解ω=f(z,t)在H×[0,T]是一族调和同胚,则对任一t∈[0,T],F(ω,t)满足

证明对任一t∈[0,T],由于ω=f(z,t)是上半平面H到复平面C内的调和同胚,在上半平面H上存在全纯函数g(z,t)和h(z,t),使得ω=f(z,t)=g(z,t)+h(z,t),并且fzzˉ(z,t)=0.

因此,具有一族调和同胚解的Lowner方程族必满足上述条件.
推论2.1设F(ω,t)∈C2(H,[0,T]),Lowner 微分方程(1)的解ω=f(z,t)是H×[0,T]上的一族调和同胚,则F(ω,0)是上半平面H的调和映射.
证明由于ω=f(z,t)是上半平面H内的一族调和同胚,则存在H×[0,T]内的全纯函数族g(z,t),h(z,t),使得

又ω=f(z,0)=z,则

当t=0 时,ω=f(z,t)的第二复伸张
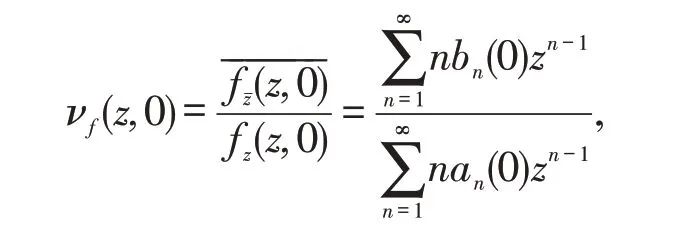
由式(3)知,νf(z,0)=0.结合定理2.1中式(2)知,Fωωˉ(ω,0)=0,因此F(ω,0)在上半平面内是调和映射.
一个自然的问题是,具有调和拟共形映射解的Lowner方程中复值连续函数F(ω,t)是否为调和映射?对于这个问题,一般调和拟共形映射来说是难于研究的. 本文中,考虑上半平面内形如ω=f(z,t)=u(x,y,t)+iy的调和拟共形映射,以这一族调和拟共形映射为解的Lowner方程,其F(ω,t)也是一族调和映射.
引理2.1设f(z,t)=u(z,t)+iv(z,t)是定义在上半平面H×[0,T]内的一族C1类K(t)-拟共形映射,K(t)是大于或等于1 且只依赖于t的非负连续函数,若v(z,t)=c(t)y,其中c(t)为非负连续函数,则对任意t∈[0,T],f(z,t)均是上半平面H内的满射且是bi-Lipschitz的.
证明因为f(z,t)=u(z,t)+iv(z,t)是一族C1类拟共形映射,则对任意t∈[0,T],下列不等式成立:

其中:Jf(z,t)是f(z,t)的Jacobian行列式,K(t)是大于1且只依赖于t的非负连续函数.
另一方面,对f(z,t)=u(z,t)+iv(z,t)分别关于求偏导得到

其中:ux(z,t),uy(z,t)分别是u(z,t)的偏导数z=x+iy∈H. 将fz(z,t),fzˉ(z,t)分别代入式(4)得到下列不等式:

显然,由式(5)可以看出

从而得到

即

又K(t),c(t)均在闭区间[0,T]内是非负连续函数,从而K(t),c(t)在闭区间[0,T]内必一致有界,由上述不等式(6)和(7)可得,u(z,t)的偏导数ux(z,t),uy(z,t)在闭区间[0,T]内也是一致有界的,即存在非负常数M,使得

再由不等式(6)知,ux(z,t)>0,(z,t)∈H×[0,T].
由v(z,t)=c(t)y与不等式(8)式可知,Jf(z,t)≠0,从而对任意t∈[0,T],f(z,t)均是满的,且f(z,t)满足Lipschitz 条件. 又因为拟共形映射的逆也是拟共形映射,可知,f-1(z,t)也满足Lipschitz 条件,即f(z,t)在H内是bi-Lipschitz的.
定理2.2设F(ω,t)∈C2(H,[0,T]) ,若Lowner 微分方程(1)在上半平面H×[0,T]内存在一族形如ω=f(z,t)=u(x,y,t)+iy的K(t)-调和拟共形映射解,则F(ω,t)在上半平面H内是一族调和映射,其中u(x,y,t)是一族连续依赖于t的上半平面H内的实值调和函数,且满足初始条件u(x,y,0)=x,K(t)(≥1)是非负连续函数. 特别地,若u(z,t)∈C2(H,[0,T]),则F(ω,t)是上半平面H内的调和拟共形形变.
证明对任意t∈[0,T],因为ω=f(z,t)=u(x,y,t)+iy是拟共形映射,则ω=f(z,t)关于z与zˉ的偏导数为

其中ux(x,y,t),uy(x,y,t)分别是u(x,y,t),z=x+iy∈H的偏导数.,显然当t=0 时,F(ω,0)是调和映射.
另一方面,对Lowner 微分方程(1)两边分别对z与zˉ求偏导,得到
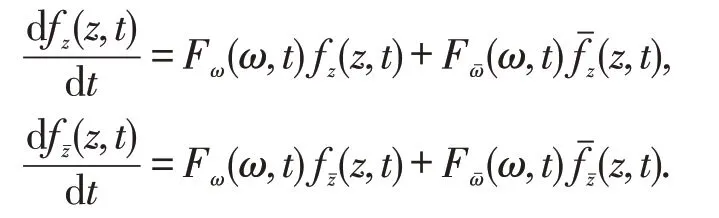
把fz(z,t),fzˉ(z,t)分别代入上述两个等式的两端,并化简得到
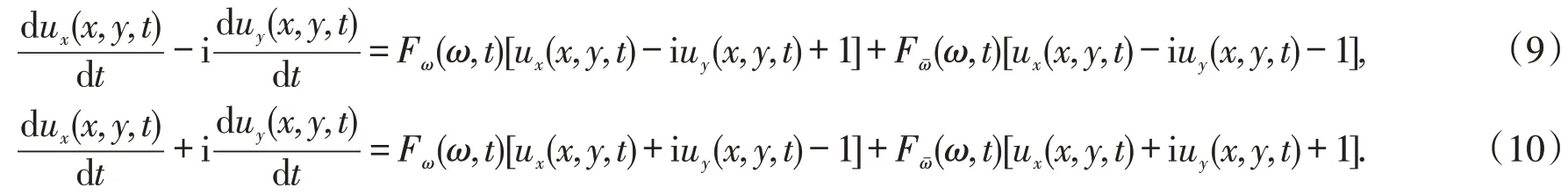
式(9)+式(10)得

式(9)-式(10)得

把式(11)代入上式得

结合式(11)和式(12)得

从式(13)(14)可看出Fω(ω,t)与Fωˉ(ω,t)互为共轭,即又因为F(ω,t)∈C2(H,[0,T]),所以F(ω,t)在H×[0,T]内的第二复伸张即F(ω,t)的第二复伸张νF(ω,t)在H×[0,T]内为全纯函数. 因此,对任意t∈[0,T],函数F(ω,t)在H内是调和的.
另一方面,由式(14)知
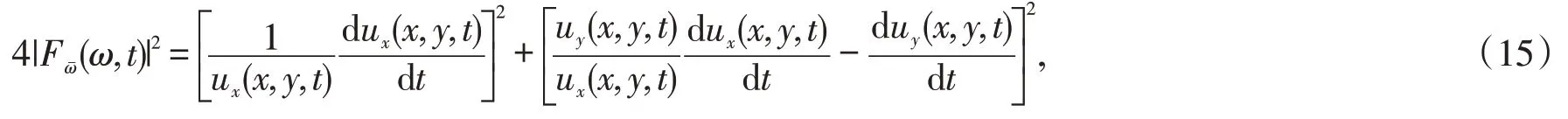
又因为ω=f(z,t)=u(x,y,t)+iy是K(t)-调和拟共形映射,由引理2.1 的证明过程知,存在非负常数M,且M >1,使得对所有的t∈[0,T],

特别地,由u(z,t)∈C2(H,[0,T])可知,对任意的z=x+iy∈H,ux(x,y,t),uy(x,y,t)关于t∈[0,T]分别是一阶连续偏导函数,于是得到在闭区间[0,T]内一致有界,即存在非负常数N,L,使得对所有的t∈[0,T],均有

将不等式(16)(17)分别代入式(15)得到
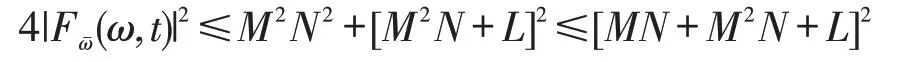
记Q=MN+M2N+L,则|Fωˉ(ω,t)|≤Q2,于是得到,若u(z,t)∈C2(H,[0,T]),F(ω,t)是上半平面H内的调和拟共形形变.

