赏析与数列前n项和有关的不等式证明

陶 蕊

(浙江省元济高级中学，314300)

数列不等式是由数列知识与不等式内容整合、交汇而成的,是高中数学的重要内容,也是初等数学与高等数学的衔接点之一．本文以高考题为例,从五种角度出发探讨与数列前n项和有关的不等式证明题的解决方案．

策略1直接求和+有界性

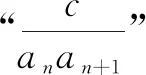
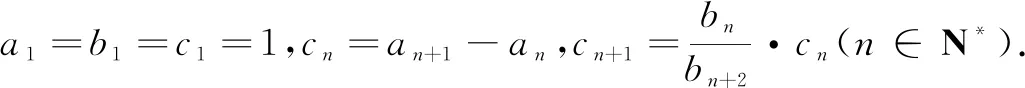
(1)略；

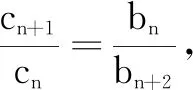
策略2单调性+最值

数列是定义在正整数集上的特殊函数,在解题时要具有函数的思想和意识．

(1)求an与bn;

(i)求Sn;

(ii)求正整数k,使得对任意的n∈N*均有Sk≥Sn.

解(1)an=2n,bn=n(n+1).(过程略)

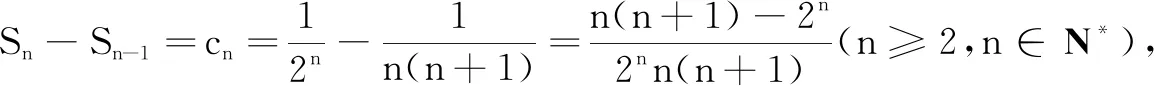
策略3放缩求和

放缩法是处理数列不等式的重要方法,其本质是利用不等式的传递性,难点是变形灵活、技巧性强．如何把握放缩的“度”是放缩的精髓所在.放缩求和目标模型常见的有等差模型、等比模型、裂项相消模型、错位相减模型、倒序相加模型这五种，其中等比模型和裂项相消模型出现的频率较高．

例3(2019年浙江高考题)设等差数列{an}的前n项和为Sn,a3=4,a4=S3.数列{bn}满足:对每个n∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列.

(1)求数列{an},{bn}的通项公式;

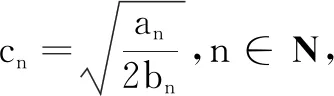
解(1)an=2n-2,bn=n2+n.(过程略)

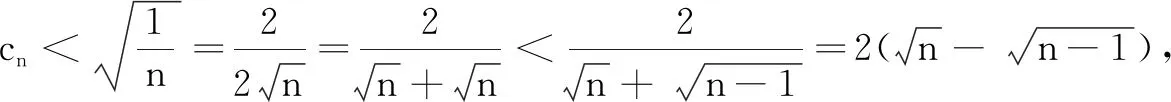
例4(2014年全国高考题)已知数列{an}满足a1=1,an+1=2an+1.

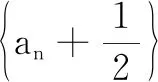
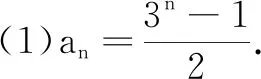
策略4数学归纳法

数学归纳法证明不等式的适用范围是遇到与正整数有关的命题,若用其他方法不容易证明,则可以考虑应用数学归纳法,关键是运用归纳假设,由n=k命题成立证明n=k+1时命题也成立．

例5题同例3.

解(1)an=2n-2,bn=n2+n.(过程略)

下面用数学归纳法证明不等式成立.

当n=1时，c1=0<2,不等式成立.

策略5综合分析法

运用综合分析的解题方法，一方面是执果索因、逆向思考问题， 在分析过程中去寻觅结论成立的一些条件(隐含条件、过渡条件等),由欲知确定需知；另一方面是由需知利用已知，充分利用已知条件进行衔接，往往会收到柳暗花明又一村的效果．

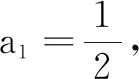
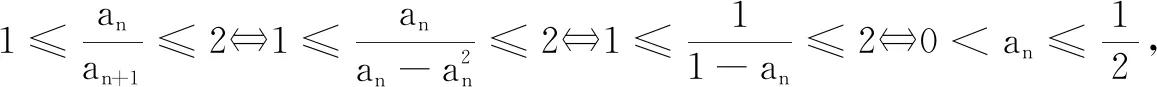
当n=1时,命题成立.

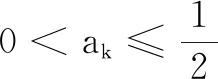
综上，命题得证.

综上,命题得证．

与数列前n项和有关的不等式证明题是高考命题的热点.虽然在思维和方法上要求高、难度大,但是只要观察已知条件的结构特征,选择合适的解题策略，此类问题即可突破．