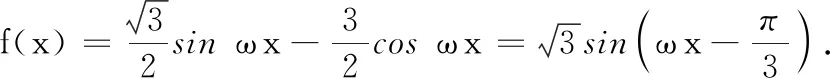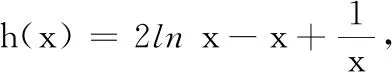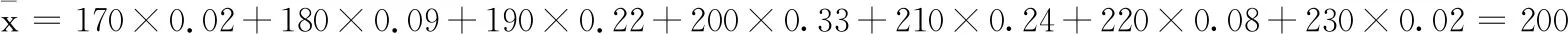高三数学综合测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1.已知集合A={x|x<1},B={x|3x<1},则( )

(A)A∩B={x|x<0}

(B)A∪B=R

(C)A∪B={x|x>1}

(D)A∩B=∅

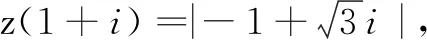
(A)-1+i (B)-1-i

(C)1+i (D)1-i

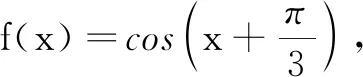
(A)f(x)的一个周期为-2π

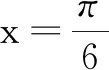
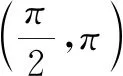
4.已知向量a,b满足|a|=5,|b|=6,并且a·b=-6,则cos〈a,a+b〉=( )

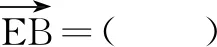
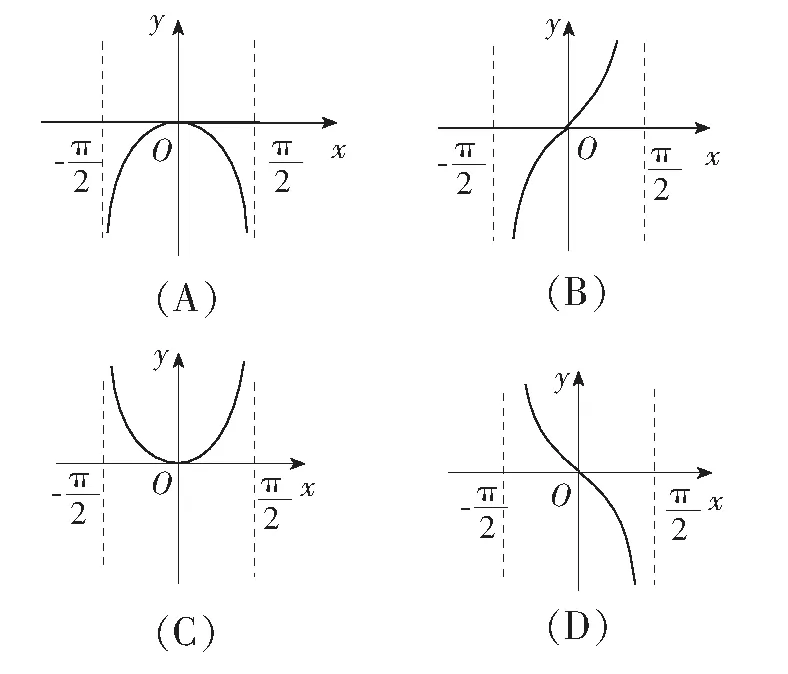
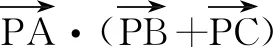
(A)(2,3) (B)(2,3]

(C)[2,3) (D)[2,3]

二、多项选择题(本大题共4小题,每小题5分，计20分)

(A)g(x)为奇函数

(B)g(x)的最小正周期为π

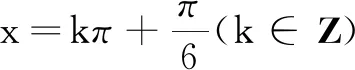
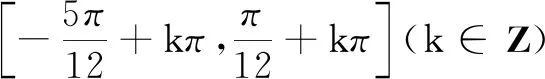
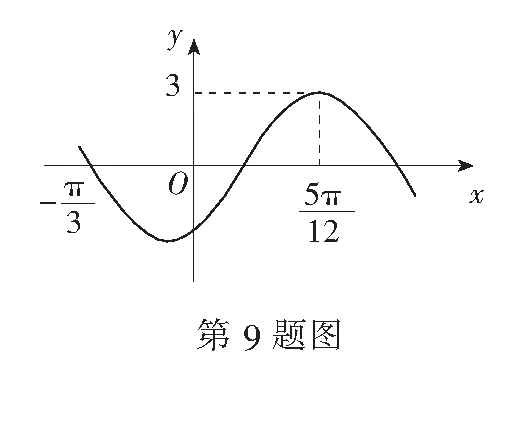
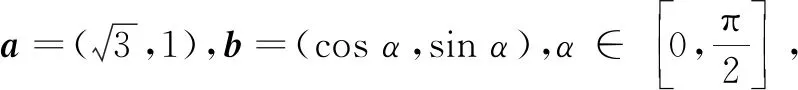
(A)|b|=1

(C)a·b的最大值为2

(D)|a-b|的最大值为3

11.已知函数f(x)=sinx-|sinx|,下列结论正确的有( )

(A)f(x)是奇函数

(B)f(x)是周期函数,且周期为2π

(C)f(x)的最小值为-2

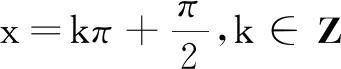
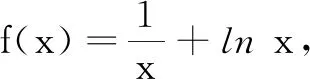
(A)f(1)是f(x)的极小值

(B)函数y=f(x)-x有且只有1个零点

(C)f(x)在(-∞,1)上单调递减

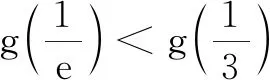
三、填空题(本大题共4小题,每小题5分，计20分)

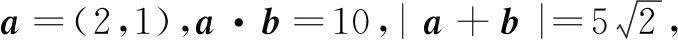
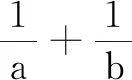
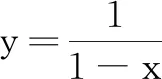
四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

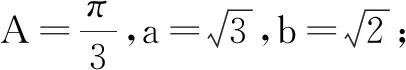
问题:在∆ABC中,角A,B,C所对的边分别为a,b,c,______,判断三角形解的情况,并在三角形有两解的情况下解三角形.

注:如果选择多个条件分别解答,按第一个解答计分.

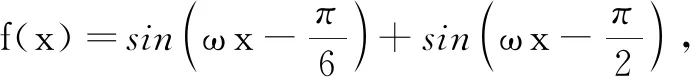
(1)求ω;

19.(本小题满分12分)已知函数f(x)=axlnx,g(x)=x2-b,若曲线y=f(x)与y=g(x)相交于P(1,0),且在点P处有相同的切线.

(1)求a,b的值;

(2)比较f(x)与g(x)的大小关系.

20.(本小题满分12分)从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:

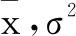
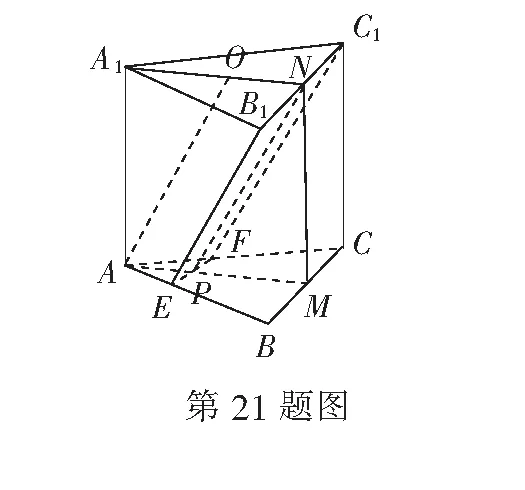
(i)利用该正态分布,求P(187.8

(ii)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数利用(i)的结果,求EX.

21.(本小题满分12分)如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.

(1)证明:MN∥AA1且平面A1AMN⊥平面EB1C1F;

(2)设O为∆A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.

22.(本小题满分12分)已知函数f(x)=emx+x2-mx.

(1)求函数f(x)的单调区间;

(2)若对于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1,求m的取值范围.

参考答案

一、单选题

1.A;2.C;3.D;4.D;

5.A;6.A;7.D;8.C.

二、多选题

9.BD;10.AC;11.BCD;12.ABD.

三、填空题

四、解答题

19.(1)由f(1)=g(1),可得12-b=0,b=1.又f′(x)=a(lnx+1),g′(x)=2x,且f′(1)=g′(1),故a=2.

s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.

(2)(i)由(1)知,Z服从正态分布N(200,150),从而P(187.8

(ii)由(i)可知,一件产品的质量指标值位于区间(187.8,212.2)的概率为0.682 6,依题意知X～B(100,0.682 6),所以EX=100×0.682 6=68.26.

21.(1)因为M,N分别为矩形BC,B1C1的中点,所以MN∥BB1.又因AA1∥BB1,故MN∥AA1.

在正三角形ABC中,因为M为BC的中点,所以BC⊥AM.

又侧面BB1C1C为矩形,故BC⊥BB1.而MN∥BB1,所以MN⊥BC.

由MN∩AM=M,MN,AM⊂平面A1AMN,得BC⊥平面A1AMN.

又B1C1∥BC,故B1C1⊥平面A1AMN.

因为B1C1⊂平面EB1C1F,所以平面EB1C1F⊥平面A1AMN.

(2)连结NP,因为AO∥平面EB1C1F,平面AONP∩平面EB1C1F=NP,所以AO∥NP.

根据三棱柱上下底面平行,其面A1NMA∩平面ABC=AM,面A1NMA∩平面A1B1C1=A1N,故ON∥AP.所以四边形ONPA是平行四边形.

设∆ABC边长是6m(m>0),则ON=AP,NP=AO=AB=6m.

在B1C1上截取B1Q=EP=m,故QN=2m.因为B1Q=EP,且B1Q∥EP,所以四边形B1QPE是平行四边形,有B1E∥PQ.

由(1)知B1C1⊥平面A1AMN, 故∠QPN为B1E与平面A1AMN所成角.

22.(1)f′(x)=m(emx-1)+2x.

若m≥0,则当x∈(-∞,0)时,emx-1≤0,f′(x)<0;当x∈(0,+∞)时,emx-1≥0,f′(x)>0.

若m<0,则当x∈(-∞,0)时,emx-1>0,f′(x)<0;当x∈(0,+∞)时,emx-1<0,f′(x)>0.

综上,f(x)在(-∞,0)单调减,在(0,+∞)单调增.

(2)由(1)知,对任意的m,f(x)在[-1,0]单调减,在[0,1]单调增,故f(x)在x=0处取得最小值.

所以,对于任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1的充要条件是

①

设g(t)=et-t-e+1,则g′(t)=et-1,易见g(t)在(-∞,0)单调减,在(0,+∞)单调增.又g(1)=0,g(-1)=e-1+2-e<0,故当t∈[-1,1]时,g(t)≤0即当m∈[-1,1]时,g(m)≤0,g(-m)≤0,即① 式成立.

当m>1时,由g(t)的单调性,得g(m)>0,即em-m>e-1,不合题意;当m<-1时,g(-m)>0,即e-m+m>e-1,不合题意.

综上,m的取值范围是[-1,1].