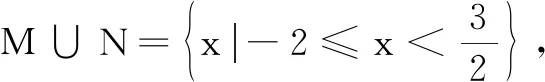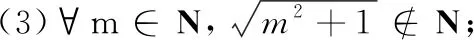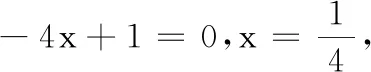高一数学测试
一、单项选择题(本大题共8小题,每小题5分,计40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果集合A={x|x2+x=0},那么( )
(A)0⊆A(B){0}∈A
(C)∅∈A(D){0}⊆A
2.已知集合A={x|x2-5x<-4},集合B={x|x≤0},则A∩(RB)=( )
(A)(-1,0) (B)(-1,4)
(C)(1,4) (D)(0,4)
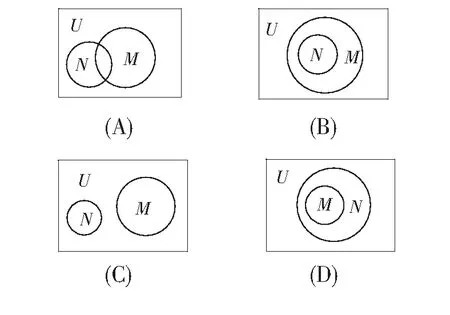
3.已知全集U=R,正确表示集合M={-2,0,2}和N={x|x2-2x=0}关系的Venn图是 ( )
4.设a>0,则“b>a”是“b2>a2”的 ( )
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
5.已知集合A={a,a2,0},B={1,2},若A∩B={1},则实数a的值为( )
(A)-1 (B)0 (C)1 (D)±1
6.已知p:4x-m<0,q:1≤3-x≤4,若p是q的一个必要不充分条件,则实数m的取值范围为( )
(A){m|m≥8} (B){m|m>8}
(C){m|m>-4} (D){m|m≥-4}
7.若关于x的方程x2-px+6=0和x2+6x-q=0的解集分别为M,N,且M∩N={2},则p+q=( )
(A)21 (B)8 (C)7 (D)6
8.取整函数:[x]=不超过x的最大整数,如[1.2]=1,[2]=2,[-1.2]=-2.取整函数在现实生活中有着广泛的应用,诸如停车收费,出租车收费等都是按照“取整函数”进行计费的.以下关于“取整函数”的性质是假命题的有( )
(A)∃x∈R,[2x]=2[x]
(B)∀x,y∈R,[x]=[y],则x-y<1
(C)∀x,y∈R,[x+y]≤[x]+[y]
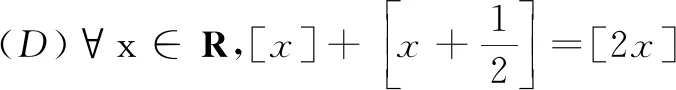
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.已知全集U=R,集合A,B满足AB,则下列选项正确的有( )
(A)A∩B=B
(B)A∪B=B
(D)A∩(UB)=∅
10.在下列命题中,真命题有( )
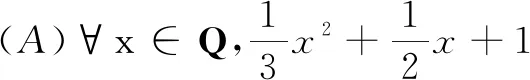
(B)∃x,y∈Z,使3x-2y=10
(C)∀x∈R,x2>|x|
(D)命题“∀x∈R,x3-x2+1≤0”的否定是“∃x∈R,x3-x2+1>0”
11.在下列结论中,正确的有( )

(B)在∆ABC中,“AB2+AC2=BC2”是“∆ABC为直角三角形”的充要条件
(C)若a,b∈R,则“a2+b2≠0”是“a,b全不为0”的充要条件
(D)若a,b∈R,则“a2+b2≠0”是“a,b不全为0”的充要条件

(A){1,3,4}为“权集”
(B){1,2,3,6}为“权集”
(C)“权集”中不一定有元素1
(D)“权集”中一定有元素1
三、填空题(本大题共6小题,13-16题每小题5分,17,18题每小题12分,计44分)
13.满足关系式{2,3}⊆A⊆{1,2,3,4}的集合A的个数是______.
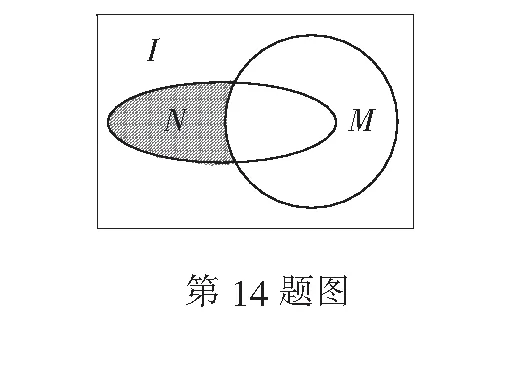
14.设全集I=R,集合M=(-1,+∞)与N=(-2,2)都是I的子集,则图中阴影部分所表示的集合为______.
15.已知A={x|x2+3x-4=0},B={x|x2-ax+a-1=0},若BA,则a的值为______.
16.甲、乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分.甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为______.
17.下列各小题中的p是q的什么条件(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”).
(1)p:x2-1=0,q:x-1=0;
(2)p:AB,q:A∩B=A;
(3)p:a,b∈R,a+b>0,q:ab>0;
(4)p:m∈(0,3),q:m∈(0,1);
(5)p:一个四边形是矩形,q:四边形的对角线相等;

(1)______;(2)______;(3)______;(4)______;(5)______;(6)______.
18.写出下列命题的否定,并判断它们的真假.
(1)∀a∈R,一元二次方程x2-ax-1=0有实根;
(2)每个正方形都是平行四边形;
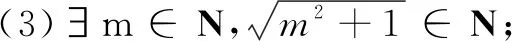
(4)∀x∈R,x2+5x=4.
(1)______;______.
(2)______;______.
(3)______;______.
(4)______;______.
四、解答题(本大题共4小题,计46分.解答时应写出必要的文字说明、证明过程或演算步骤)
19.(本小题满分10分)设全集为R,A={x|3≤x<7},B={x|2 (1)求A∩B; (2)求CR(A∪B). 20.(本小题满分12分)设集合M={x|(x+a)(x-1)≤0}(a>0),N={x|4x2-4x-3<0}. (2)若(CRM)∪N=R,求实数a的取值范围. 21.(本小题满分12分)已知集合A={x|(k+2)x2+2kx+1=0}. (1)当k=2时,求A; (2)若A是空集,求k的取值集合; (3)若集合A至多只有2个子集,求k的取值集合. 22.(本小题满分12分)已知集合A={x|1 (1) 若A∪B=B,求实数m的取值范围; (2)若“x∈A”是“x∈B”的充分不必要条件,求实数m的取值范围; (3)若A∩B=∅,求实数m的取值范围. 参考答案 一、单项选择题 1.D;2.C;3.B;4.A; 5.A;6.B;7.A;8.C. 二、多项选择题 9.BD;10.ABD;11.AD;12.BD. 三、填空题 13.4;14.(-2,-1]; 15.2;16.{48,51,54,57,60}. 17.(1)必要不充分; (2)充分不必要;(3)既不充分又不必要;(4)必要不充分;(5)充分不必要;(6)充要. 18.(1)∃a∈R,一元二次方程x2-ax-1=0没有实根;假命题. (2)存在一个正方形不是平行四边形;假命题. (4)∃x∈R,x2+5x≠4; 真命题. 四、解答题 19.(1)由题意,A∩B={x|3≤x<7}. (2)由题意,A∪B={x|2 (2)因为a>0,M={x|-a≤x≤1},则有RM={x|x<-a或x>1}.又(RM)∪N=R,所以 (3)若集合A至多只有2个子集,则A为空集,或A为只含有一个元素的集合. 当A是空集时,由(2)知k的取值集合为(-1,2). 综上,k的取值集合为{-2}∪[-1,2]. 22.(1)由A∪B=B,得A⊆B.于是 解得m≤-2.所求实数m的取值范围为(-∞,-2]. (2)由题意,有AB.于是或解得m<-2或m≤-2.故所求实数m的取值范围为(-∞,-2]. (3) 当A∩B=∅时,有B=∅或B≠∅. 综上,实数m的取值范围为[0,+∞).