一道初等数学题解法的高观点思考

徐文艺

(江苏省扬州大学旅游烹饪学院营养2001班，225000)

一、引言

转眼进入大学校园已两个多月了,通过《高等数学》课程的学习,笔者接受了现代数学的一些思想,对中学数学产生了新的认知,又触发了我对数学的研究兴趣．记得曾做个如下一道题.

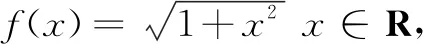
这是一道能激发学生思维火花的典型习题.在初步理解“数学是研究数、形和关系的科学”的观点后,对该题进行了再思考,获得了新认识，本文据此对这道题再作一些探索．

二、思考

1.囿于数,技巧解困

在已知函数解析式的条件下比较两个数的大小,如果局限在“数”的认知范围,常用的解题思路是“作差比较”或“作商比较”．

解法1(平方比较)

作差比较大小,由于题设中带绝对值的两个数直接作差求解时变形去绝对值比较麻烦,故采取平方比较．先估计大小，明确方向不妨取a=0,b=1时,知|f(a)-f(b)|小,这样明确方向．于是

|f(a)-f(b)|2<|a-b|2

⟺2ab0,

可知恒有|f(a)-f(b)|<|a-b|成立．

解法2(作商比较)

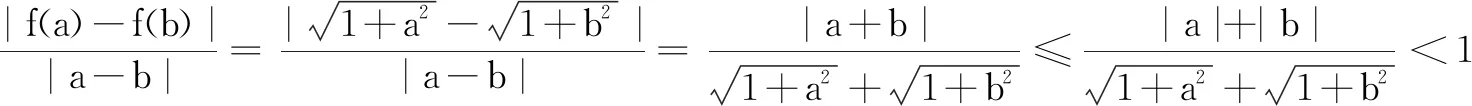
评注从作商比较过程看,分子有理化、放缩变形是可能会遇到的困难．

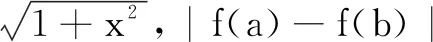
2.迁移形,思路开阔

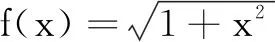
解法3(联系平面几何)

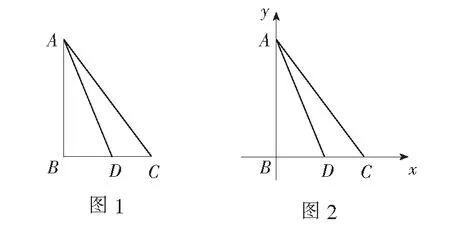
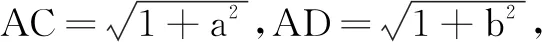
解法4(联系解析几何)

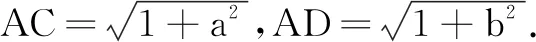
解法5(联系向量)

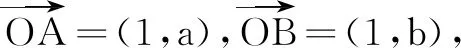
解法6(联系复数)

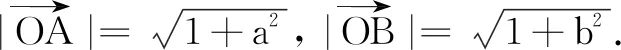
3.放眼关系,思维提升

如果从现代数学的研究对象“关系”角度考虑本题的解法,还可以得到以下三种解题方法．

解法7(联系解析几何)

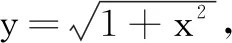
解法8(换元法)

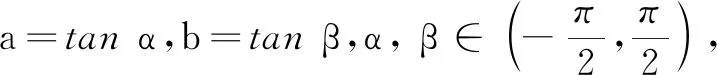
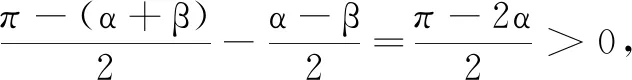
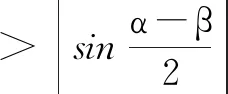
解法9(利用中值定理)

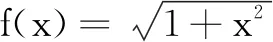
三、启示

记得语文老师曾说过,好戏是“捏”出来的.我感到好题也需要不断揣摩,站在不同的观点,就会有不同的感受.解决数学问题时观其形、究其本,无论从哪个角度观察,其根本是数学思想方法及其灵活运用．