定点定值问题的曲线系探究与本源揭示

侯书红

(中央民族大学附属中学昆明五华实验学校，650032)

探究解析几何的定值问题时,常规思路往往是联立方程组、运用韦达定理解决问题,计算起来有时相当复杂.而曲线系方程体现了整体处理、参数变换的数学思想,为简化运算提供了有效工具.本文以两道试题为例,展示从曲线系方程入手能快速解题,并通过一般性探究其本源,期望对读者能有所启迪.

一、问题提出

与文[1]类似,我们不难得到如下结论

结论已知圆锥曲线方程为f(x,y)=0,曲线上四点对应的四边形的四条边方程为l1(x,y)=0,l2(x,y)=0,l3(x,y)=0,l4(x,y)=0,则经过这四点的二次曲线系方程可表示为l1(x,y)l2(x,y)+λf(x,y)=μl3(x,y)l4(x,y).

二、问题解析

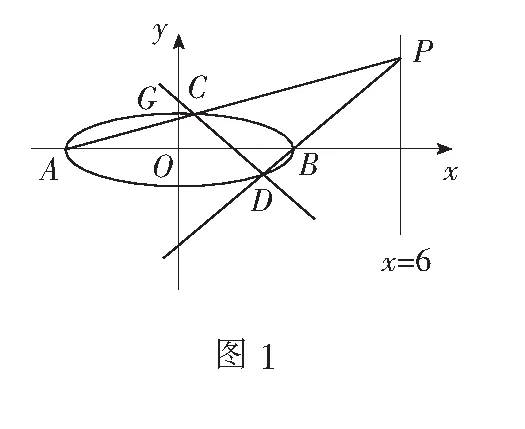
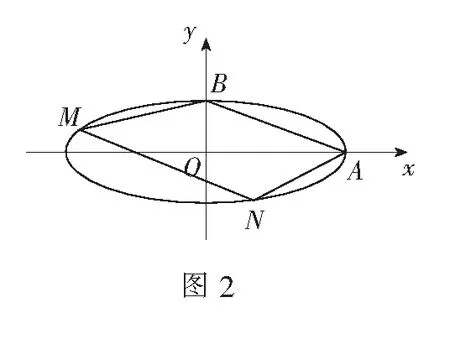
(1)求E的方程;

(2)证明:直线CD过定点.

对例1进行本源探究,可得如下变式：

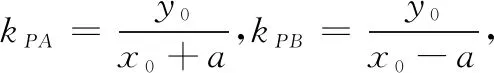
证明如图2,易知直线AN,BM,AB的方程分别为y=k1(x-2),y=k2x+1,x+2y=2.又MN∥AB,可设直线MN的方程为x+2y+m=0,过A,B,M,N四点的曲线系方程为(k1x-y-2k1)(k2x-y+1)+λ(x2+4y2-4)=μ(x+2y-2)(x+2y+m),整理得(k1k2+λ)x2+(1+4λ)y2-(k1+k2)xy+(k1-2k1k2)x+(2k1-1)y-(2k1+4λ)=μx2+4μy2+4μxy+(μm-2u)x+(2mμ-4μ)y-2mμ.

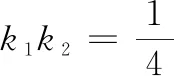
对例2进行本源探究,可得如下变式：

从以上两例可以看出,通过曲线系方程能比较简捷地探究出问题的本源,有利于解析几何问题的解决.