用递推数列处理无穷多级电阻问题

刘向东 冯心怡

(上海市闵行中学，200240)

“宇宙间万物的总规律,其本质就是数的严整性和和谐性．”物理学科中也处处包含着数学之美．在学习无穷多级电阻时,可能会产生这样一个问题:将无穷多级电阻从某一级处截断,所得前半部分的总电阻是多少呢?让我们先探究一类递推数列的通项公式,再通过几道例题欣赏数学和物理这两个学科之间的相关之美．

一、一类递推数列的通项公式

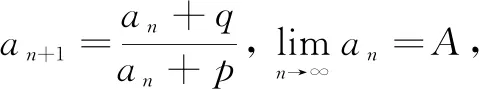
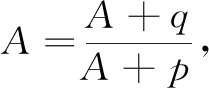
二、应用举例

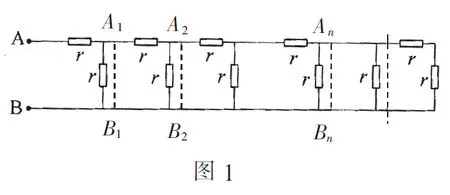
例1如图1是由无限个阻值均为1Ω的电阻按一定规律组成的网络.若从图中A1B1处沿虚线将网络截断,A,B间阻值为R1(Ω);若从A2B2处沿虚线将网络截断,A,B间阻值为R2(Ω);…;依次类推,从AnBn处沿虚线将网络截断,A,B间阻值为Rn(Ω).试求Rn的通项与极限.

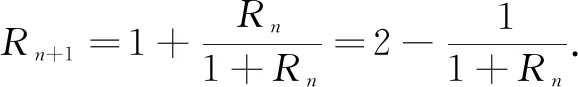
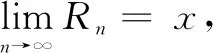
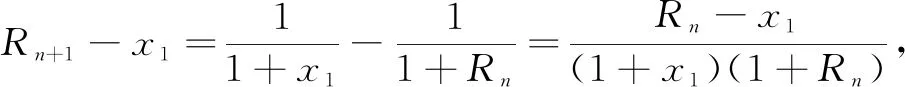
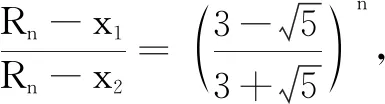
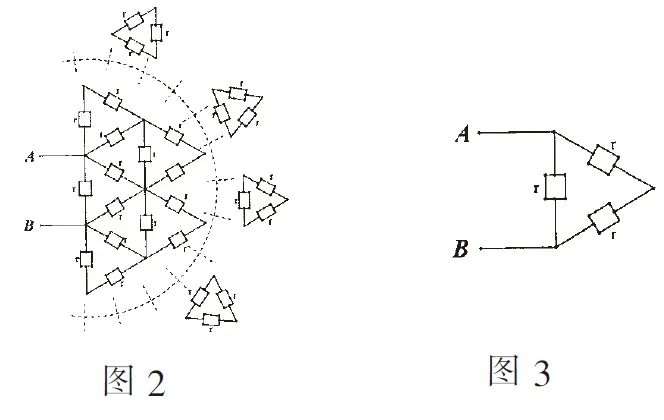
例2如图2的无穷多级电阻网络,每个电阻为r=1Ω,记A,B间电阻为R；图3为R1状态,图4为R2状态,图5为R3状态.每次在最外围边的电阻上并联2个电阻.试求Rn的通项与极限.

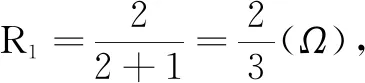
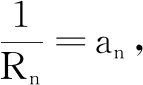
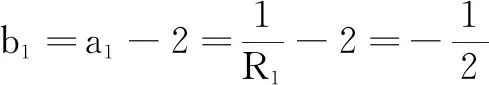
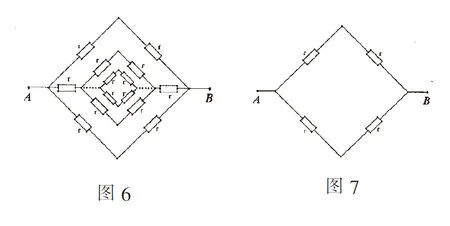
例3如图6是一个无穷多级电阻网络,记A,B间电阻为R,图7为R1状态,图8为R2状态. 每次在A,B内部并联一个小正方形形状的导电线框(线框电阻不计),正方形的每条边上都有一个阻值为r=1Ω的电阻. 依此类推,直到Rn,试求Rn的通项与极限.

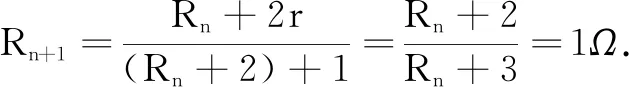
对物理无穷多级电阻问题,采用数学中数列的知识来探讨也是一件很有趣的事．对于含有无穷多级电阻的电路,我们可将其分解,运用递推的思想来理解该电路,这就是学科间相辅相成的和谐之美．