改进的永磁同步电机模型预测直接转矩控制策略

苏丹丹，李浩东，尹延周，李志远，苏建文

(1. 河北大学 质量技术监督学院，河北 保定 071002；2. 河北长安汽车有限公司，河北 定州 073000)

直接转矩控制(direct torque control，DTC)根据定子磁链矢量所在的分区及定子磁链滞环调节器和转矩滞环调节器的输出选择合适的空间电压矢量，具有结构简单、对电机参数变化鲁棒性强、转矩响应速度快等优点[1-2].但由于滞环控制器自身原因，逆变器开关频率不恒定，且每个采样周期只作用单一电压矢量，不可避免地导致较大的转矩和定子磁链脉动[3].为此国内外学者提出了很多改进的直接转矩控制方案，如基于空间矢量调制的直接转矩控制[4]、基于占空比调制的直接转矩控制[5-6]、模型预测直接转矩控制[7-9]等，其中模型预测直接转矩控制具有实现简单、控制灵活、动态响应好等优点而被广泛关注[10-11].

1 永磁同步电机直接转矩控制策略

1.1 转矩与定子磁链观测器

直接转矩控制以电机实际输出的电磁转矩Te与定子磁链ψs为反馈值，通过建立观测器模型来估计Te与ψs.

在永磁同步电机转子两相旋转dq坐标系下建立的转矩观测器模型为

(1)

式中，ψd、ψq分别为dq轴的定子磁链，id、iq分别为dq轴的电流，P为电机极数.

基于电流模型法建立的定子磁链ψs观测器模型，如下：

(2)

式中，λf为永磁体主磁通，Ld、Lq为dq轴电感.

1.2 双滞环调节器

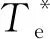
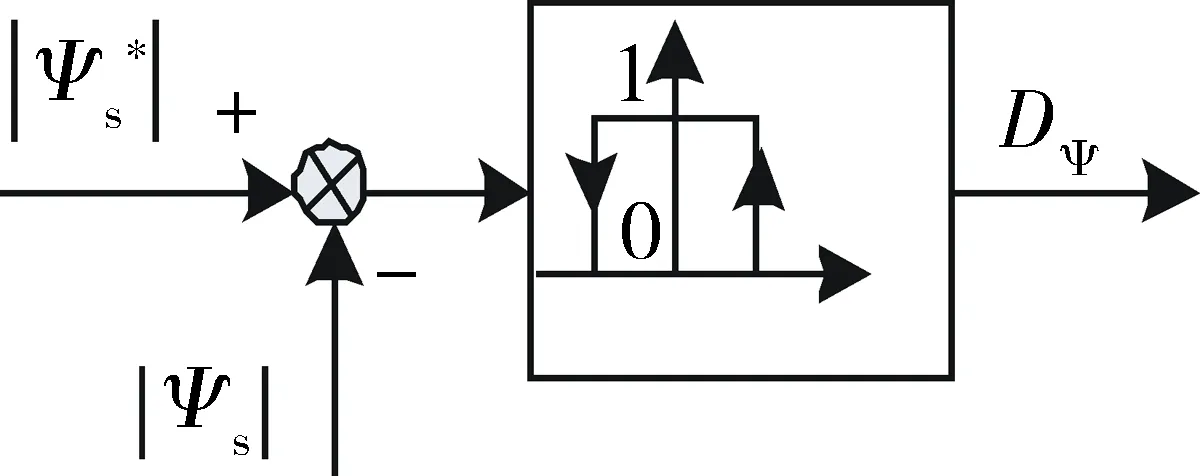
图1 定子磁链滞环Fig.1 Hysteresis controller of stator flux

图2 转矩滞环Fig.2 Hysteresis controller of torque

1.3 电压矢量选择表

两电压电平源型逆变器根据其上下桥臂的开关状态，可以输出8种不同的空间电压矢量，其中包括6种非零电压矢量和2种零电压矢量[12].在直接转矩控制中，为了能准确地确定某瞬时定子磁链的空间位置，将定子静止坐标系均匀分成6个区域，分别标以θ(1)、θ(2)、…、θ(6).在电机运行中，要求定子磁链|Ψs|满足

(3)

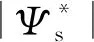
表1中列出了6个区域内逆变器输出的电压矢量，可根据定子磁链矢量所在的分区及转矩和定子磁链滞环调节器的输出选择合适的电压矢量.通过分析表1可知，当转矩误差在滞环调节范围内时，直接转矩控制策略会选择零矢量.

1.4 直接转矩控制原理

永磁同步电机直接转矩控制是根据定子磁链矢量所在的分区及定子磁滞环调节器和转矩滞环调节器的输出选择合适的空间电压矢量，其控制原理如图3所示.

表1 电压矢量选择

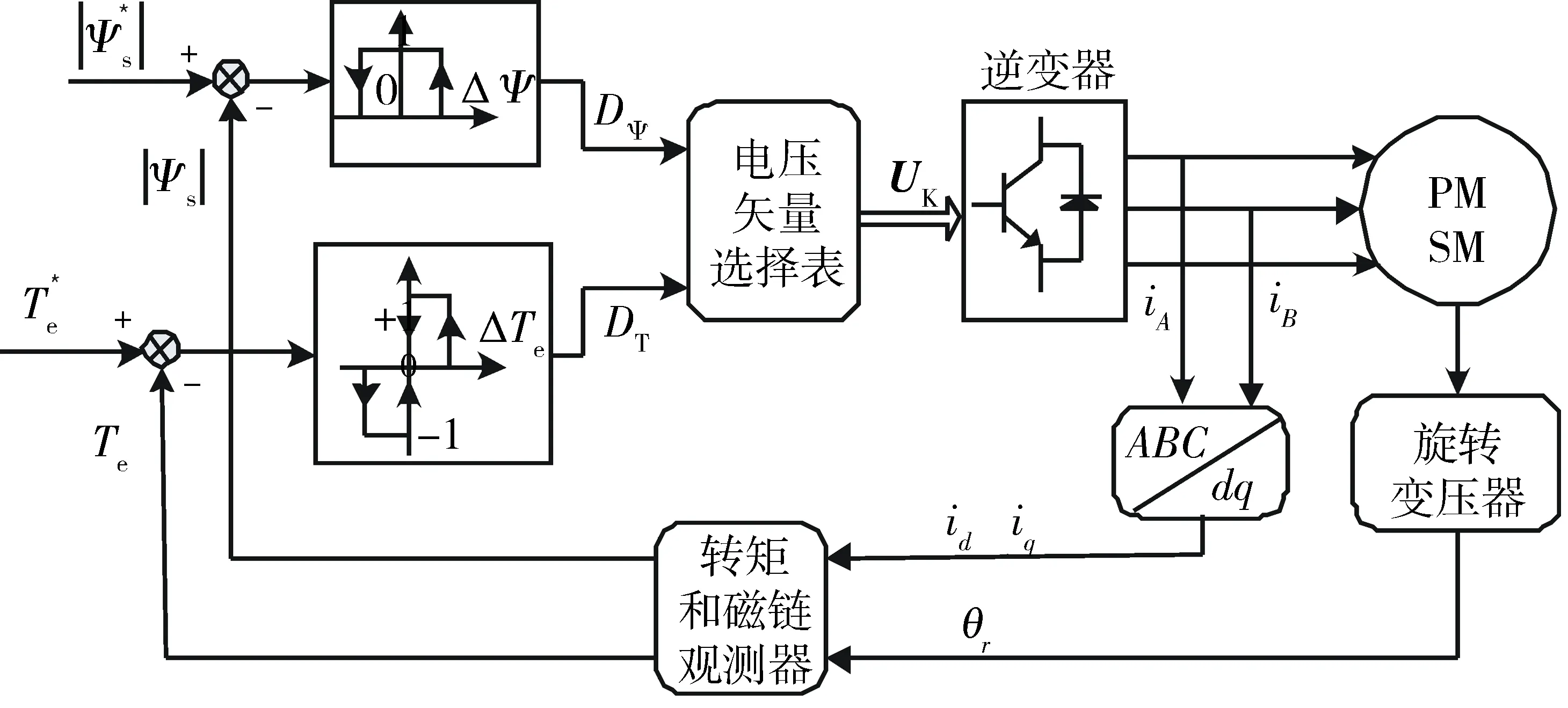
图3 直接转矩控制原理Fig.3 Block of direct torque control

2 传统模型预测直接转矩控制策略

模型预测直接转矩控制是以转矩和定子磁链为控制目标，对每种电压矢量作用下的转矩和定子磁链分别进行预测，再根据转矩和定子磁链的综合误差最小的原则利用评价函数选择出最优电压矢量作为下一时刻电机的输入[3].图4为传统模型预测直接转矩控制的流程.

图4 传统模型预测直接转矩控制流程Fig.4 Flow chart of traditional model predictive direct torque control

模型预测直接转矩控制的过程可分为以下4个步骤.

1)测量：通过传感器测量永磁同步电机相电流、直流母线电压、转子位置等信号.

2)预测：基于永磁同步电机的离散数学模型预测逆变器在7个电压矢量作用下的转矩和定子磁链.

3)评价：分别计算7个电压矢量作用下的评价函数，并选择使评价函数值最小的电压矢量为最优电压矢量.

4)应用：逆变器输出最优电压矢量.

随着预测步长的增加，系统的计算量会成倍增加.为了简化计算，本文选择的预测步长为1.

模型预测直接转矩控制的评价函数是使转矩与定子磁链能够跟踪各自的参考值，同时为了平衡转矩误差和定子磁链误差在最优电压矢量选取过程中所占比重，引入了相应的权重因子对评价结果进行调节.常用的模型预测直接转矩控制评价函数为

(4)

式中，λT和λψ分别为转矩误差和定子磁链误差的权重因子.

3 改进的模型预测直接转矩控制策略

为了降低传统模型预测直接转矩控制的计算工作量，本文在直接转矩控制策略与传统模型预测直接转矩控制理论的基础上，提出了改进的模型预测直接转矩控制策略.

3.1 永磁同步电机在dq两相旋转坐标系下的离散数学模型

永磁同步电机在dq两相旋转坐标系下离散的电压方程可表示为

(5)

其中

式中，Rs为永磁同步电机相电阻，Ts为采样周期，Uq(k)、Ud(k)为k时刻dq轴电压，iq(k)、id(k)为k时刻dq轴电流，ωr(k)为转子的电角速度.

离散的永磁同步电机定子磁链方程为

(6)

式中，ψd(k)和ψq(k)分别为k时刻d轴和q轴磁链，ψs(k)为k时刻定子磁链.

离散的输出转矩方程为

(7)

式中，Te(k)为k时刻输出电磁转矩.

电机的运动方程为

(8)

式中，J为转动惯量；ωm(k)为k时刻转子机械角速度；TL(k)为k时刻负载转矩；F为摩擦因数.

3.2 零电压矢量作用下永磁同步电机转矩与定子磁链预测

永磁同步电机在零电压矢量作用下的离散数学模型为

(9)

式中，iq(k+1)、id(k+1)为经过一步延时补偿后k+1时刻的dq轴电流；iq0(k+2)、id0(k+2)为基于永磁同步电机模型预测出的零电压矢量作用1个采样周期后的k+2时刻的dq轴电流.

在零电压矢量作用下k时刻永磁同步电机的输出转矩和定子磁链为

(10)

(11)

根据以上公式可知，在零电压矢量的作用下电机输出转矩和定子磁链均变化平缓，且绝缘栅双极型晶体管(IGBT， insulated gate bipolar transistor)无开关动作，因此零电压矢量的使用能够降低转矩脉动和逆变器的开关损耗.

3.3 零电压矢量的选择

在零电压矢量作用下，转矩和定子磁链的预测值与参考值之间的误差定义为

(12)

式中，ΔTe0(k)是零电压矢量作用下k时刻预测的转矩与参考值之间的误差；Δψs0(k)是零电压矢量作用下k时刻预测的定子磁链与参考值之间的误差.

在零电压矢量选择过程中，应设定一个合理的转矩误差与定子磁链误差阈值(DT0，Dψ0).如果零电压矢量作用下的预测转矩和定子磁链与给定参考值之间的误差均在允许范围内，则逆变器输出的最优电压矢量为零电压矢量，否则需进一步在非零电压矢量中选择最优矢量，如式(13)所示.

(13)

当需要选择非零电压矢量时，可根据直接转矩控制定子磁链的分区及电压矢量选择表，选择最优非零电压矢量.

如果在最优电压矢量选择过程中忽略零电压矢量，即仅基于定子磁链的分区及电压矢量选择表选择最优非零电压矢量，该最优非零电压矢量作用下所产生的转矩误差和定子磁链误差分别为

(14)

(15)

式中，ΔTeopt(k)是最优非零电压矢量作用下k时刻预测的转矩与参考值之间的误差；Δψsopt(k)是最优非零电压矢量作用下k时刻预测的定子磁链与参考值之间的误差；Teopt(k)是最优非零电压矢量作用下k时刻预测的转矩；ψsopt(k)是最优非零电压矢量作用下k时刻预测的定子磁链.

在电机控制中使用零电压矢量过多会导致电机输出的平均转矩降低，使用零电压矢量过少会使IGBT开关频率明显增大.因此，转矩误差与定子磁链误差阈值的合理选择具有重要意义.为了降低转矩误差与定子磁链误差，转矩误差与定子磁链误差阈值可由式(16)计算.

(16)

3.4 改进的模型预测直接转矩控制策略

图5为所提出的改进的模型预测直接转矩控制原理框图.首先，驱动系统在每个采样周期均通过传感器测量电流信号与转子位置信号，并进行一步延时补偿；其次，基于永磁同步电机的数学模型，预测零电压矢量作用下的电磁转矩和定子磁链；然后，计算预测值与参考值之间的误差，并将该误差与其阈值进行比较.如果转矩误差与定子磁链误差均在阈值范围内，则最优电压矢量为零电压矢量；否则，根据转矩误差与定子磁链误差，基于传统直接转矩控制理论中定子磁链的分区和电压矢量选择表，选出最优的非零电压矢量.最后，将逆变器输出的最优电压矢量作用于驱动系统.

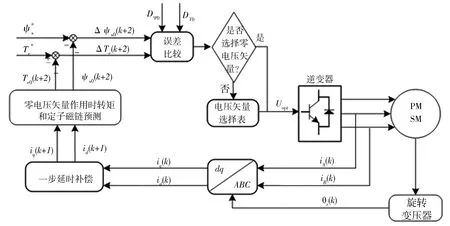
图5 改进的模型预测直接转矩控制原理Fig.5 Improved model predictive direct torque control

本文所提出的改进的模型预测直接转矩控制能够明显降低计算工作量.首先，只需要预测零电压矢量作用下的输出转矩和定子磁链，需预测的电压矢量的个数为1，降低了计算工作量；其次，本文所提出的改进的模型预测直接转矩控制控制策略是根据转矩与磁链误差，利用了传统直接转矩控制理论中定子磁链的分区和电压矢量选择表确定出最优非零电压矢量，因而不需要计算评价函数，同时省去了评价函数中权重因子繁杂的调节工作.

4 基于MATLAB的仿真实验

永磁同步电机参数如表2所示.图6和图7为直接转矩控制、传统的模型预测直接转矩控制与改进的模型预测直接转矩控制的MATLAB仿真结果对比图.仿真过程中，直流母线电压为200 V，转速为400 r/min，参考转矩为60 N·m，信号采样频率为20 kHz.直接转矩控制中转矩滞环的偏差为2 N·m，定子磁链滞环的偏差为0.01 Wb；传统的模型预测直接转矩控制策略中定子磁链的权重因数为500，转矩的权重因数为1；改进的模型预测直接转矩控制中，零电压矢量作用时预测转矩与参考转矩的偏差设为2 N·m，预测定子磁链与参考定子磁链的偏差设为0.01 Wb.

表2 永磁同步电机参数

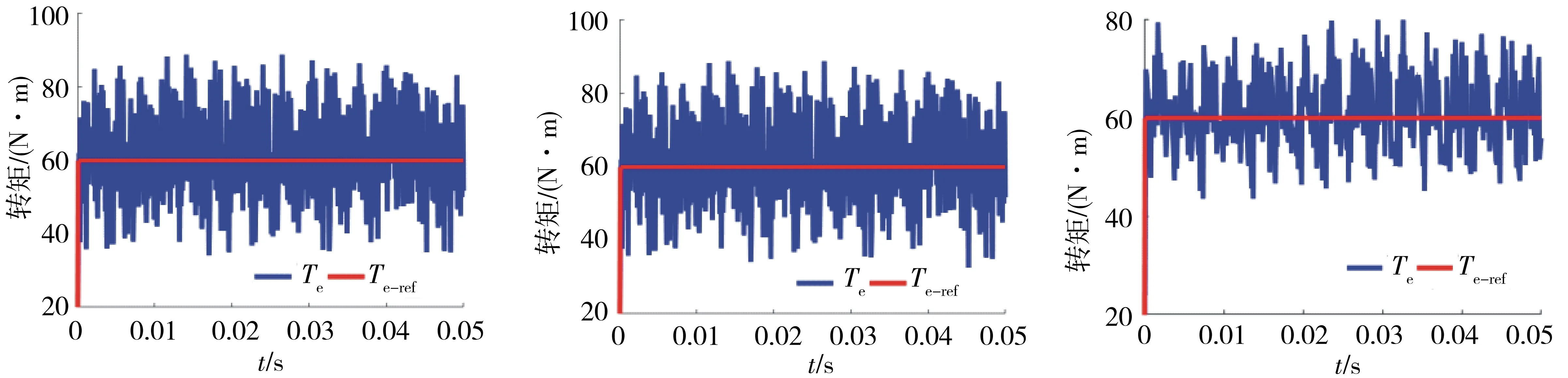
a.直接转矩控制；b.传统的模型预测直接转矩控制；c.改进的模型预测直接转矩控制.图6 输出转矩对比Fig.6 Contrast of torque

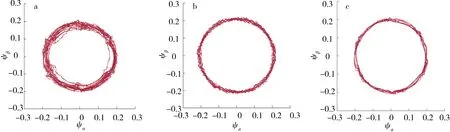
a.直接转矩控制；b.传统的模型预测直接转矩控制；c.改进的模型预测直接转矩控制.图7 αβ轴磁链对比Fig.7 Contrast of αβ-axis flux

图6为直接转矩控制、传统的模型预测直接转矩控制和改进的模型预测直接转矩控制的输出转矩.由图6可知，改进的模型预测直接转矩控制继承了直接转矩控制和传统模型预测直接转矩控制响应速度快的优点，并能够准确追踪参考转矩.图7为3种控制策略定子磁链的仿真结果.传统的模型预测直接转矩控制在评价函数中引入权重因子，因此定子磁链能很好地跟踪参考值.直接转矩控制与改进的模型预测直接转矩控制电压矢量的选择过程中更多的以转矩为主，因此定子磁链的跟踪效果稍差.

图8为直接转矩控制、传统的模型预测直接转矩控制与改进的模型预测直接转矩控制的实际运行时间对比图.仿真过程中，MATLAB的仿真时间设置为0.1 s.其中直接转矩控制实际用时1.118 59 s，传统的模型预测直接转矩控制实际用时1.217 49 s，改进的模型预测直接转矩控制实际用时1.162 s.与传统的模型预测直接转矩控制相比，改进的模型预测直接转矩控制降低了计算工作量，仿真过程中实际用时明显减少.

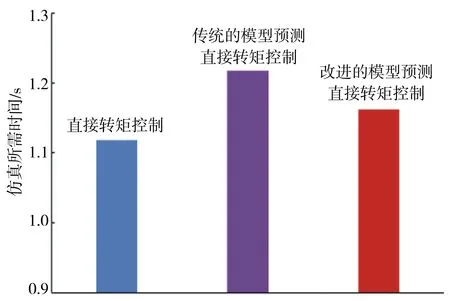
图8 MATLAB实际运行时间对比Fig.8 Contrast of running time

5 结论

本文依据永磁同步电机直接转矩控制和模型预测直接转矩控制的基本原理，研究了零电压矢量作用下的转矩误差和定子磁链误差，在此基础上提出了改进的模型预测直接转矩控制策略.改进的模型预测直接转矩控制只需要预测零矢量作用下的转矩和定子磁链，根据转矩和定子磁链误差与其阈值的比较结果确定最优电压矢量是否选择零电压矢量；当最优电压矢量为非零电压矢量时，利用了传统直接转矩控制理论中定子磁链的分区和电压矢量选择表确定出最优非零电压矢量.最后基于MATLAB建立了永磁同步电机直接转矩控制、传统模型预测直接转矩控制和改进的模型预测直接转矩控制的仿真模型.仿真结果表明，永磁同步电机采用改进的模型预测直接转矩控制策略时，电机转矩和定子磁链均能快速准确地跟踪参考值.