交联点官能度和网络缠结效应对凝胶薄膜屈曲失稳的影响

李涛，杨庆生

(北京工业大学 机械工程与应用电子技术学院，北京 100124)

水凝胶是一种具有亲水基团三维网络结构的聚合物.“小激励大响应”是这种智能软材料的典型特征.由于其对多种环境(如温度[1]、离子[2]、pH[3]、磁场[4]等)的刺激产生智能反应行为，因此受到了广大学者的关注.当前，随着医疗科技和电子技术的飞速发展，由水凝胶薄膜构成医疗设施和电子产品应运而生并得到了快速发展.这些器件的工作环境往往处于复杂的耦合多物理场中，受外界条件和凝胶自身材料属性共同影响，在这种复杂环境中凝胶膜的屈曲是常见的现象.由化学膨胀引起的软材料不稳定性现象，特别是屈曲行为通常是影响智能器件性能的主要失效机制.近年来，对于处在多物理场中凝胶大变形和凝胶屈曲失稳问题被中外学者广泛研究.2008年Hong等[5]推导了在化学-力学耦合作用下水凝胶发生大变形自由能方程，基于此理论，Liu等[6]探讨了水凝胶一维杆件和二维水凝胶薄膜的屈曲行为.但是此理论基于水凝胶完美交联假设，并未考虑构成凝胶的三维网络微结构在耦合变形过程中发生的变化.张校维等[7]将此理论进一步推广，考虑凝胶网络中未交联的滑动链的影响探讨了滑动链对凝胶屈曲的影响，但是依旧未考虑凝胶拓扑网络结构交联点官能度在化学-力学耦合过程中发挥的作用.Yang等[8]和Li等[9]综合考虑构成水凝胶三维网络结构的滑动链，交联点官能度影响以及大变形时网链的非高斯性，进一步拓展了理论推导了更符合实际情况的自由能公式.本文将基于此理论探讨凝胶微结构参数和外部环境对耦合场中水凝胶薄膜屈曲的影响.

1 水凝胶化学-力学耦合变形本构关系

水凝胶具有在化学-力学耦合场作用因为溶胀发生大变形的性质.对于中性水凝胶，在此过程中产生2种形式的自由能：一部分是由于凝胶网络伸展产生的弹性能；另一部分是由于凝胶网络与溶剂分子混合产生的混合能.根据Flory-Huggins聚合物溶液理论，水凝胶在此过程中的自由能可以表示为

W=Welastic+Wmixing,

(1)

其中，Welastic表示大变形情况下化学交联链与滑动链在共同作用产生的弹性自由能[9]，Wmixing表示聚合物网络与溶剂结合的混合自由能[8].中性水凝胶自由能表示为

(2)

其中，Nc、Ns、Cs分别为化学交联链、滑移链和溶剂的物质的量，R为普适气体常数，T为热力学温度，Ii(i=1,2,3)表示非线性连续介质力学中右Cauchy-Green张量C的主不变量，δ是一个衡量聚合物网络链的平均轮廓长度的值[10]，f是交联点官能度，η是滑动参数，υs为溶剂分子摩尔体积.

定义水凝胶溶胀比为J，由于固体聚合物和溶剂均不可压缩，因此

(3)

通过Legendre变换，可以得到巨正则自由能密度函数[5]

(4)

将公式(2)、(3)带入公式(4)，得到化学-力学耦合的自由能密度函数，引入化学势的影响.

水凝胶是一类超弹性材料，在化学-力学耦合作用的刺激下产生响应，发生大变形，这种大变形行为可用超弹性材料的本构理论研究.根据Yang等[8]关于响应性水凝胶在多物理场下的一般理论框架的研究，水凝胶的第二PK应力可以表示为

(5)

柯西应力张量σ可以表示为[11]

(6)

其中

(7)

(8)

将公式(7)、(8)带入公式(6)可得到柯西应力张量具体形式.

2 2D无脱层水凝胶膜-弹性基层合结构屈曲问题解析解

本文旨在研究蒙附在弹性基体上的水凝胶薄膜在化学-力学耦合场作用下发生无脱层屈曲行为的临界条件以及相应水凝胶微结构的影响.根据蔡晓苏等[12]的研究结果，薄膜的表面屈曲临界波长等受到弹性模量，泊松比以及薄膜厚度影响.由于水凝胶不可压缩性，其泊松比可以确定等于0.5，因此本文只关注凝胶弹性模量的影响.

水凝胶的弹性模量随耦合场中外界条件变化.为了求解水凝胶随环境变化的弹性模量，建立如图1所示模型.在化学-力学耦合场中将初始伸长量为λ0=1.5的无限大水凝胶薄膜固定在刚性基体上，在此基础上减小外界溶液化学势，使水凝胶薄膜在z方向自由伸长直至溶胀达到平衡状态，对应伸长率为λ，对应应力为Sz=0.根据公式(8)，Sz可表示为

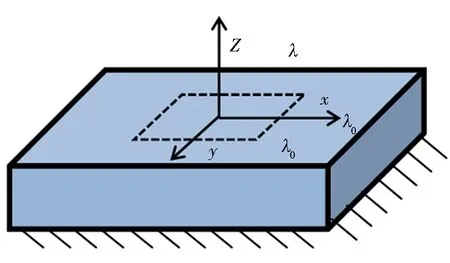
图1 刚性基体上水凝胶薄片的约束膨胀示意Fig.1 Schematics of the constrained swelling of a blanket gel layer attached to a rigid substrate

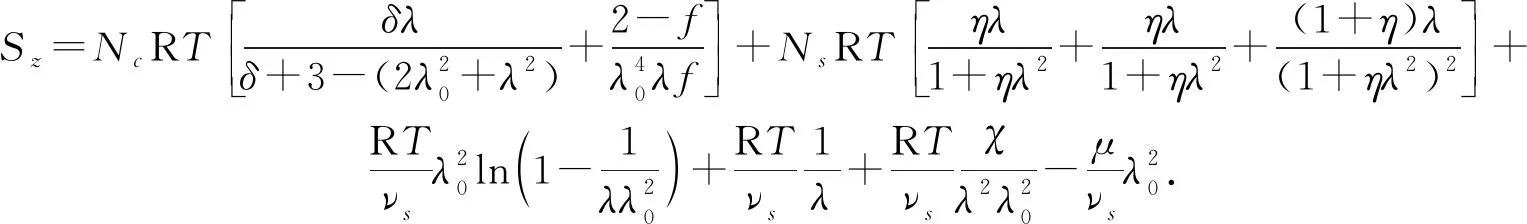
(9)

由于刚性约束，凝胶在x-y面内始终保持原始伸长率λ0，对应产生等双轴应力

(10)

将公式(9)，(10)联立可以求解得到关于等双轴应力关于伸长率的函数

(11)

作为一种超弹性材料，水凝胶增量模量可以表示为应力对应变的偏导数[6]

(12)

水凝胶在x-y平面伸长率保持λ0不变，根据公式(9)可求得水凝胶对应增量模量

(13)

为了研究凝胶薄膜屈曲问题，建立一个如图2所示模型平面应力模型：无限大的水凝胶薄膜附着在弹性基底上，初始厚度为h，层合结构在垂直于x-z面的方向上的宽度为b(b>>h).如图2a所示，凝胶薄膜贴附基体，当吸水溶胀膨胀但不发生屈曲时，处于平面均匀压应力状态.随着溶胀持续进行屈曲发生如图2b所示，对于宽度远大于厚度的水凝胶薄膜只在x方向失稳.当凝胶膜发生屈曲时，波长通常远大于厚度，因此可以采用von Karman弹性非线性板理论对凝胶膜进行建模[13].

定义z方向挠度为，则薄膜/基底结构屈曲形成的波形具有如下的形式[14]

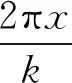
(14)

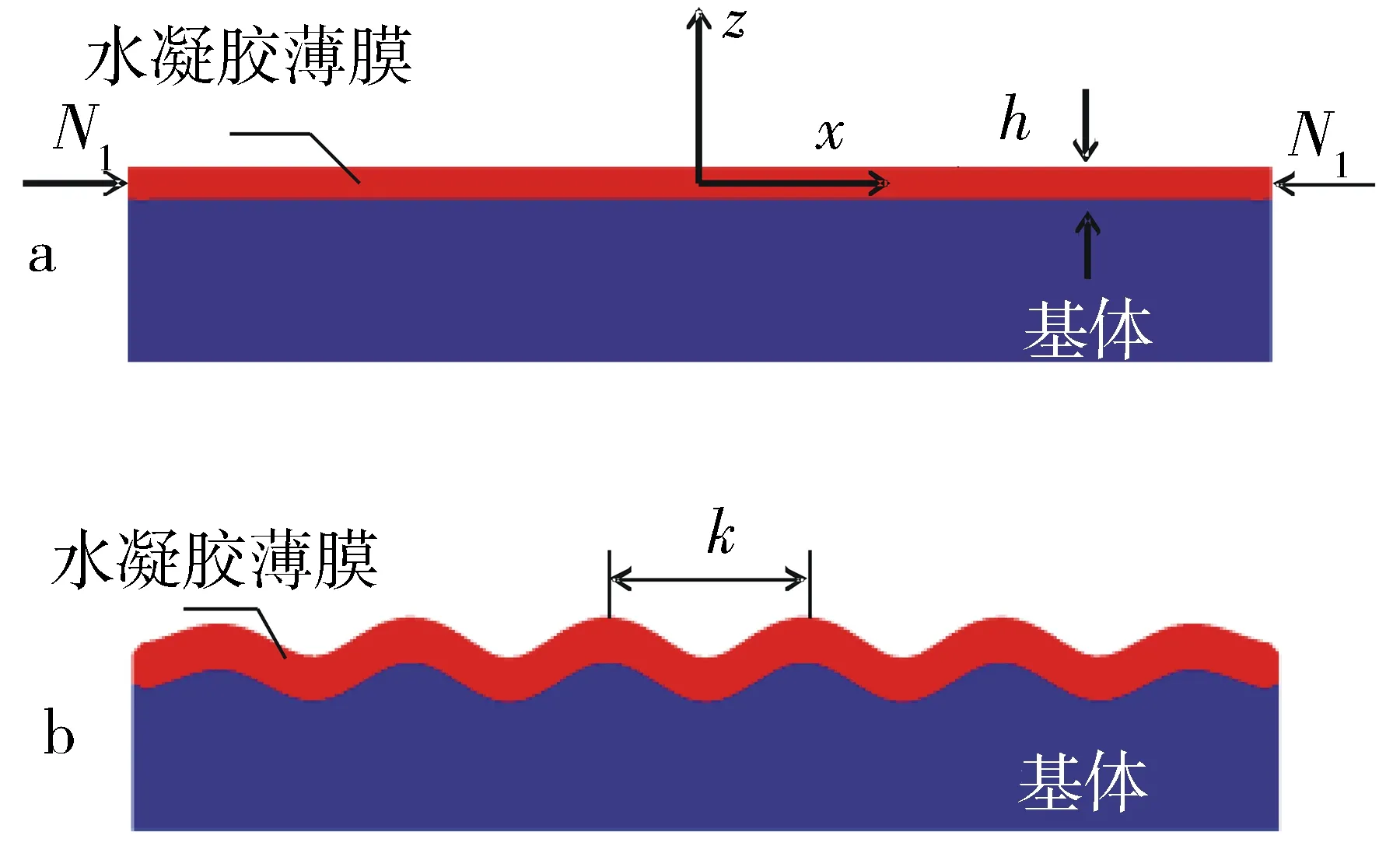
a.薄膜屈曲后;b.薄膜屈曲后.图2 二维水凝胶薄膜无脱层屈曲示意Fig.2 2D schematic diagram of delampless buckling of hydrogel films

其中k和wm分别为屈曲薄膜的波长和波峰值，薄膜和弹性基底间法向应力与变形相关，可以相应的表示为

(15)

控制凝胶薄膜挠度的von Karman弹性非线性公式可以写成[15]

D4w-(N1)2w=-bq，

(16)

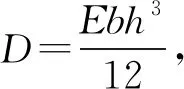
(17)

凝胶薄膜屈曲的临界压应力N1(N1=σ1bh)可以通过公式(17)求得

(18)

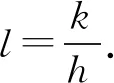
(19)

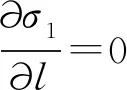
(20)

(21)

图3展示了在不同的滑动参数η和官能度f下临界波长随外界溶液化学势能的变化趋势.图3中可以看出，在交联点官能度f为定值时，临界波长和临界应力与滑动参数η呈负相关，且在化学势较小时影响明显；并且随着η增大，其对薄膜屈曲的临界应力影响变小.而在滑动参数η为定值时，临界波长与官能度f也呈负相关，低官能度条件下这种影响更为明显.

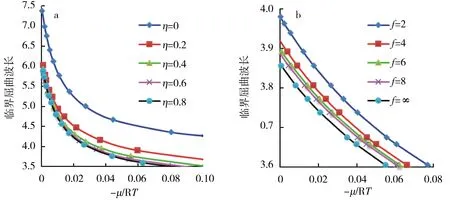
a.滑动参数变化；b.水凝胶交联点官能度变化.图3 不同微结构参数下临界波长与外界溶液化学势能的关系Fig.3 Variations of the critical wave length of a gel with the chemical potential of the external solution for different microstructural parameters

图4展示了与图3相同条件下不同的滑动参数η和官能度f对无量纲临界应力(除以NcRT得到)随外界溶液化学势能变化的影响，得到结果与图3展示的结果类似.

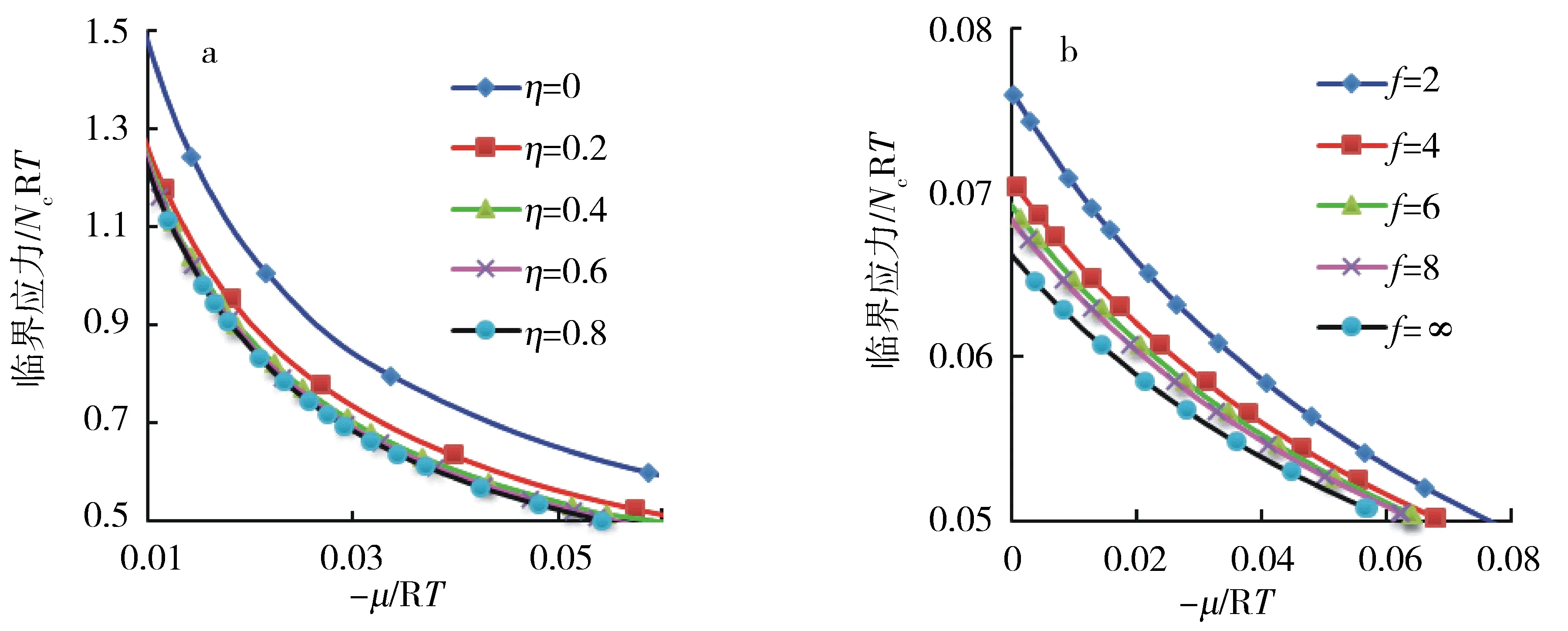
a.滑动参数变化；b.水凝胶交联点官能度变化.图4 不同微结构参数下归一化临界应力与外界溶液化学势能的关系Fig.4 Variations of the normalized critical stress of a gel with the chemical potential of the external solution for different microstructural parameters

3 结论

本文发展了一种综合考虑水凝胶网链真实情况的自由能密度函数，引入了与水凝胶网络结构相关的滑动链滑动参数，交联点官能度等微结构参数影响.在此基础上，通过解析方法求解了水凝胶薄膜/弹性基体结构在化学-力学耦合场中发生无脱层屈曲时的临界条件，得到如下结论：1)水凝胶薄膜的屈曲行为受外部化学环境影响，当水凝胶所处外界化学势降低，水凝胶的临界屈曲波长和应力均发生减小；2)水凝胶薄膜的临界屈曲应力和屈曲波长随着水凝胶缠结网链的滑动参数增加而减小，且这种影响在滑动参数较小时比较明显；3)水凝胶薄膜的临界屈曲应力和屈曲波长与水凝胶交联拓扑网络链的官能度有关，在相同的外部条件下，官能度越小临界屈曲应力和波长越小.

这种理论上的分析可以为在耦合场中应用的复杂凝胶薄膜结构，如入阵列透镜、心脏膜片、柔性电子设备的应用和制作提供相关理论依据.