弦支穹顶结构预应力张拉摩擦损失影响分析

郄禄文，徐辰昱，刘静，赵若旭，陈宗学

( 1.河北大学 建筑工程学院，河北 保定 071002；2.河北建设集团股份有限公司 钢结构分公司，河北 保定 071052)

弦支穹顶结构是一种在近几年发展迅速的杂交空间结构，它由上部刚性的单层网壳和下部柔性的索撑体系组成[1]，结构体系受力合理，可充分发挥材料性能，且可减少用钢量，经济适用性强[2].弦支穹顶结构从上部单层网壳到下部索撑体系张拉施工再到形成完整结构，其成形过程经历巨大变化.对于该类结构体系预应力的有效施加和传递是实现结构设计的重要技术，而采用张拉环索的方式对结构施加预应力时，索撑节点处因滑移摩擦产生预应力损失值大小的确定又是结构成形理论中需重要研究的内容.工程实践表明对于弦支穹顶结构体系无论采用哪种预应力张拉方式，预应力损失都是客观存在的[3].文献[4-5]实验结果表明采用张拉环索的方式施加预应力时，环索滑移引起每圈每个索撑节点平均预应力损失8%～10%，因此在进行该类结构预应力张拉全过程分析时若不考虑预应力损失的影响，其计算结果会与结构实际受力状态产生一定的差异，故研究预应力损失对结构体系的影响是十分必要的.目前，对于索撑节点滑动索的研究主要有以下几种方法：1)利用自由度耦合和变刚度弹簧单元法[3]，该方法在弦支穹顶环索张拉施工的全过程中因弹簧单元的刚度随施工步的进行而变化造成求解步骤烦琐；2)非线性接触分析[4]，该方法需采用精细的单元划分才能实现，计算量大也不便于在整体结构中实现；3)滑移索单元法[6-10]，仅文献[10]推导的索单元可考虑摩擦影响，但因滑移刚度计算十分复杂不易于实际工程应用；4)摩擦力补偿法[11]，其缺点是未考虑拉索的滑移方向；5)冷冻-升温法[12-13]，文献[12]通过虚加温度的方法经反复迭代调整索长直至张拉点两侧索力平衡，但此方法计算量大、难于收敛；6)文献[13]克服文献[12]不足，根据滑轮力学原理、利用广义逆的概念推导考虑索撑节点滑移摩擦的迭代算法易于在工程实际中实现.索撑节点的材料、设计、加工制作、施工等有关因素均会影响预应力张拉过程中索撑节点间的摩擦因数大小，但目前关于弦支穹顶结构索撑节点处滑移摩擦因数的取值对施工张拉过程中整体结构受力性能的影响还鲜有报道.本文基于文献[13]改进的预应力摩擦损失计算方法，以2022年冬奥会比赛场馆之一——河北北方学院体育馆的弦支穹顶屋盖为工程背景，利用ANSYS单元生死法及多时间步连续分析技术，研究索撑节点取不同摩擦因数时对弦支穹顶结构环索张拉全过程的影响，主要分析随各张拉步进行时屋盖各圈环索预应力、索撑节点预应力损失、撑杆及拉杆应力、网壳结构整体变形等变化规律，以期为同类结构施工提供参考.

1 工程概况

河北北方学院体育馆占地面积11 390 m2，总建筑面积26 352.4 m2，屋顶平面投影为双轴对称的类圆角矩形，平面尺寸为长轴90.99 m、短轴83.774 m，屋面矢高6.558 m，屋盖周边由32个球铰支座安装于下部钢筋混凝土牛腿柱上，整体效果如图1所示[14].弦支穹顶屋盖由上部单层网壳和下部索撑体系组成，上部单层网壳采用凯威特型和联方型组合布置网格形式，下部索撑体系由5圈环向拉索、6圈径向拉杆和竖向撑杆组成，屋盖结构如图2所示.屋盖构件和材料规格见表1，表中E表示杨氏模量，fy表示屈服强度，LG1～LG6为自内向外的6圈拉杆，HS1～HS5为自内向外的5圈环索.

图1 河北北方学院体育馆效果Fig.1 Renderings of Hebei North University gymnasium

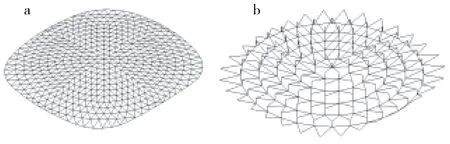
a.上部单层网壳；b.下部索撑体系.图2 屋盖结构Fig.2 Roof structure

表1 构件及材料规格

2 有限元模型建立

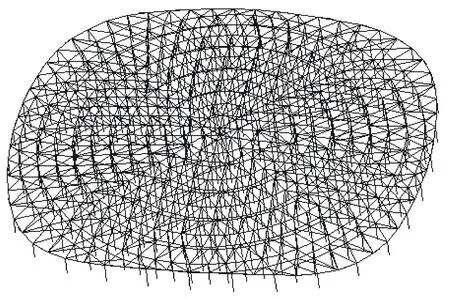
图3 有限元分析模型Fig.3 Finite element analysis model

利用有限元分析软件ANSYS建立河北北方学院体育馆弦支穹顶屋盖模型，上部单层网壳采用Beam188单元，环索采用只受拉的Link10单元，径向拉杆及竖向撑杆均采用Link8单元，网壳焊接球及索夹自重均采用质量单元Mass21，胎架采用只受压的Link10单元，球铰支座采用三向铰接约束，有限元分析模型如图3所示.计算时结构钢材采用理想弹塑性本构模型，考虑几何非线性和应力刚化效应.根据设计要求采用环向索张拉法在结构中成形所需的预应力值，应用单元生死法“杀死”和“激活”功能实现按施工顺序对环索施加预应力[15].

3 张拉过程分析

河北北方学院体育馆弦支穹顶屋盖下部环索张拉点数HS1和HS2为4个、HS3为6个、HS4和HS5为8个，张拉点位置及环索滑移方向如图4所示.预应力张拉分2批：第1批张拉在网壳成形和下部索撑体系安装完毕及满堂脚手架支撑条件下，由外至内依次张拉各圈环索至90%预应力设计值，第2批张拉在卸载胎架条件下，由内至外依次张拉各圈环索至100%预应力设计值，分别为46、136、404、657、2 108 kN.

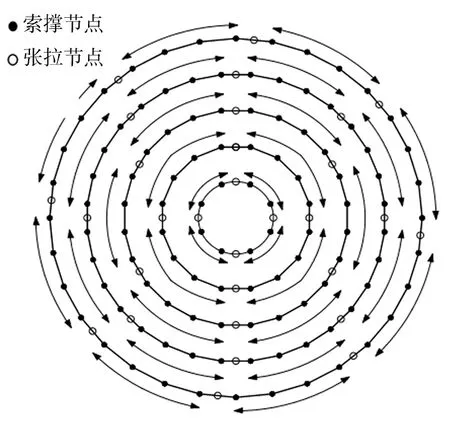
图4 张拉点及索滑移方向(箭头指示)Fig.4 Tensed-points’ position and directions of slipping cable(indicated by arrow)

参考文献[4，13]若张拉时钢夹片和索体间没有相对滑移，节点接触面间理论摩擦因数可取0.03；若节点构造完全不符合设计要求，张拉时夹片与索撑节点之间咬合，聚四氟乙烯片失去效果，此种情况索体与索撑节点间的摩擦因数约为0.3，甚至更大.基于以上理论及实验结果，本文索撑节点处分别取摩擦因数为0.03、0.1、0.2、0.3及0.4，以“降温法”[13]对环索施加预应力，采用正向分析的分级张拉方法模拟施工.计算时，考虑索撑节点两侧环索存在摩擦滑移平衡关系，同圈环索内力由张拉点向两侧递减，当两张拉点间环索最低预应力值达到设计值5%误差范围内，即认为环索张拉满足设计要求.

3.1 张拉过程环索预应力变化

根据施工张拉步要求，经过第1批由外圈至内圈5步张拉、第6步卸载胎架及第2批由内圈至外圈5步张拉合计11个施工步，得出索撑节点取5个不同摩擦因数时各圈环索在每一个施工步的最高预应力均值，如图5所示，图中最高预应力均值指同圈索张拉点间环索最高预应力的平均值.

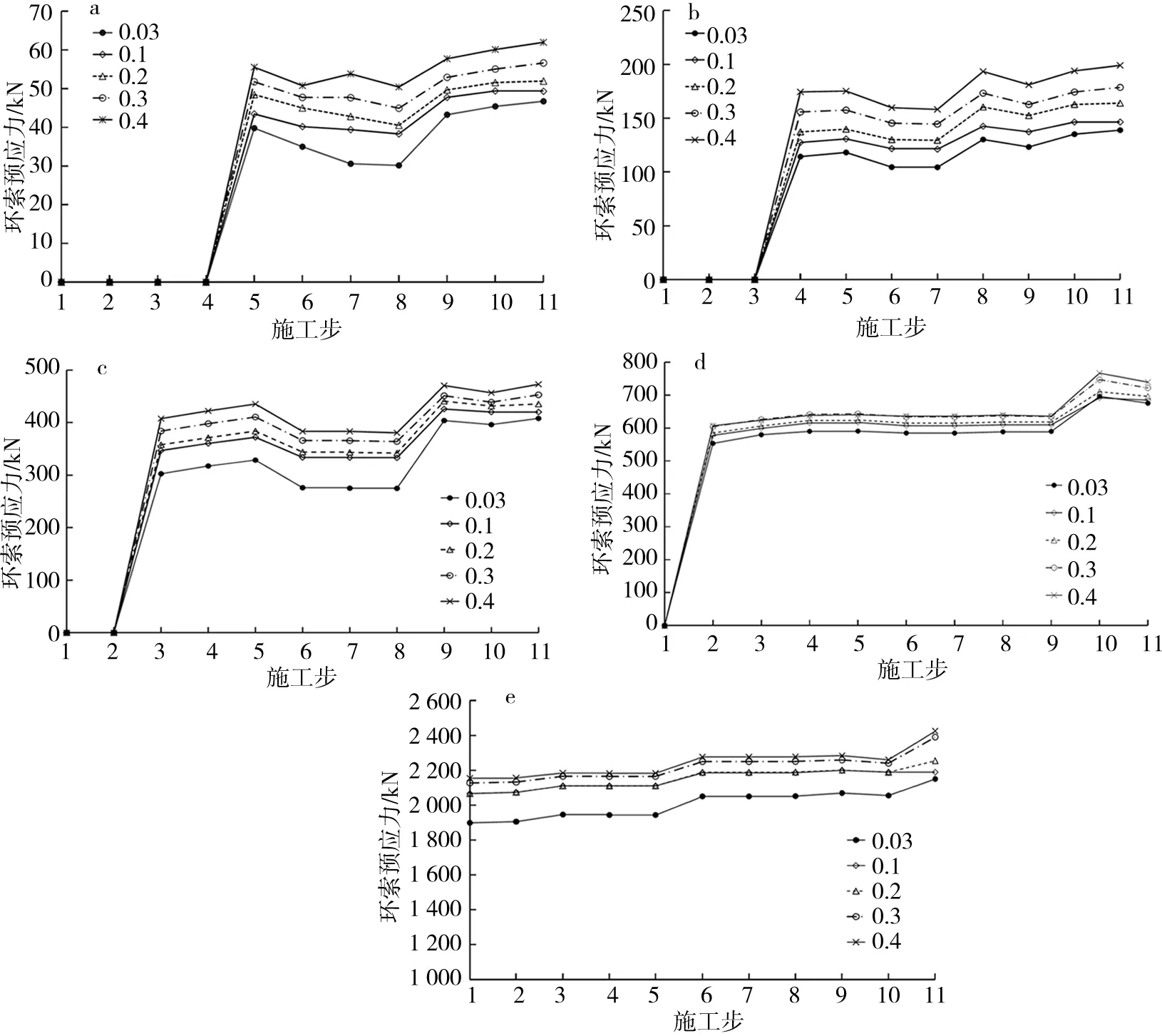
a.HS1环索预应力;b.HS2环索预应力; c.HS3环索预应力;d.HS4环索预应力; e.HS5环索预应力.图5 环索预应力-施工步变化曲线Fig.5 Prestress of cable-construction step curves

由图5可看出：1)在张拉全过程中，随索撑节点摩擦因数增大环索预应力在对应施工步逐渐增大，取5种不同摩擦因数时各圈环索预应力变化趋势基本一致，这表明摩擦因数的取值大小仅影响环索预应力大小，不改变其预应力分布模式.2)第1批张拉阶段，各圈环索在对应张拉步处获得预应力，未张拉环索处于松弛无预应力状态，说明单元生死法的计算方法符合实际施工过程.3)第6步为弦支穹顶结构卸载胎架，落架后第1～4圈环索预应力均下降，平均降幅依次为8.51%、8.32%、11.91%、1.25%，但第5圈环索预应力在卸载胎架后增大，即该圈环索处于继续“张紧”状态，当取不同摩擦因数时其环索预应力平均增幅在3.54%～5.5%之间.4)第2批张拉阶段，各圈环索预应力在张拉结束时均呈不同幅度增大，以摩擦因数取0.03计算模型的环索预应力为例，由内至外各圈环索预应力增长分别达51.92%、33.03%、52.74%、15.57%、4.90%. 5)张拉阶段因相邻圈环索张拉施工时相互影响明显，所有环索会在张拉时出现新的动态内力平衡状态，如外圈环索的张拉会使相邻内圈环索预应力略微减小出现松弛，所以对环索预应力要作较为精确地控制，且在张拉施工时应持续监测环索预应力变化.

3.2 张拉完成时环索预应力

屋盖结构张拉完成时，同圈环索所有张拉点处的最高预应力均值如表2所示.图6和图7给出各圈环索张拉完成时最高预应力偏差和索撑节点平均预应力损失随摩擦因数不同的变化情况，图中最高预应力偏差指同圈环索张拉点间环索最高和最低预应力平均值之差与环索预应力设计值之比，索撑节点平均预应力损失指同圈环索最高预应力偏差与索撑节点数之比.

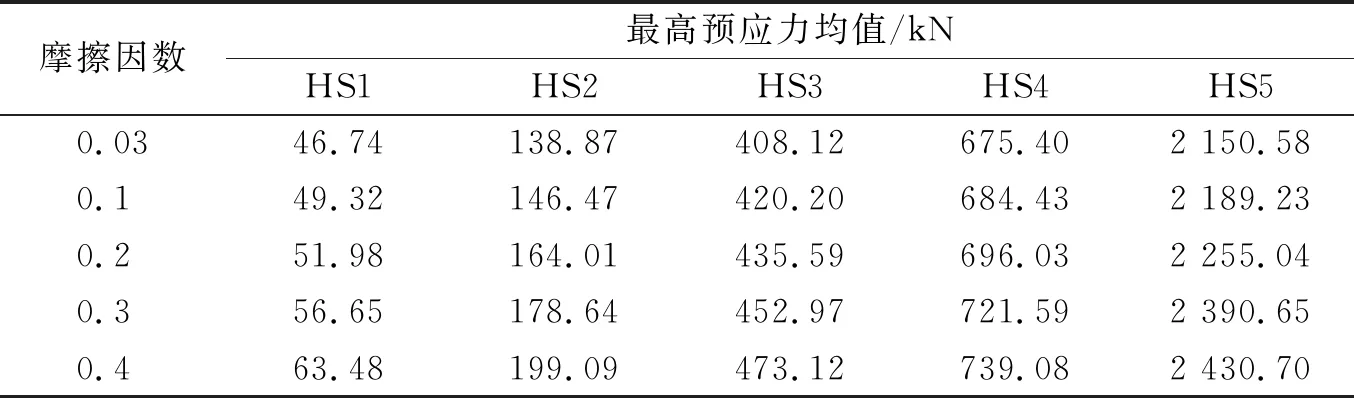
表2 张拉完成时环索最高预应力均值

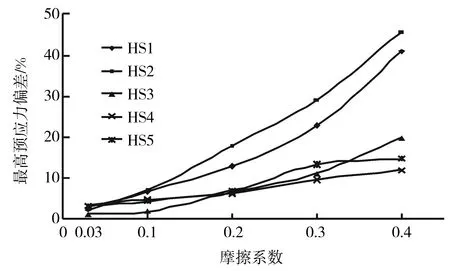
图6 张拉完成时环索最高预应力偏差 Fig.6 Maximum prestress deviation of cable after tension

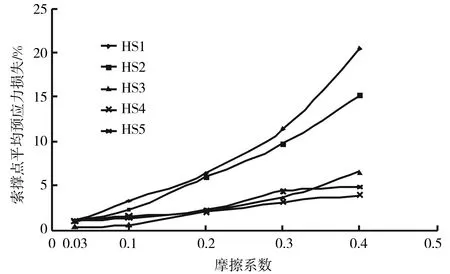
图7 张拉完成时节点平均预应力损失Fig.7 Loss of the average prestress of joints

由表2、图6和图7可看出：1)当各圈环索最低预应力均值达到预应力设计值要求时，随着索撑节点摩擦因数增大，环索最高预应力均值、预应力偏差以及索撑节点平均预应力损失都不断增大.2)在弦支穹顶屋盖张拉施工中，若钢夹片和索体间没有相对滑移即摩擦因数取0.03时，5圈环索最高预应力偏差仅为1.15%～3.23%之间；若夹片与索撑节点之间咬合且聚四氟乙烯片失去效果，摩擦因数取0.4时5圈环索最高预应力偏差达到11.94%～45.57%，这表明通过降低索撑节点与环索间的摩擦因数可极大地降低环索实际预应力与设计预应力的偏差.3)第1～2圈环索最高预应力偏差和节点平均预应力损失均大于相同摩擦因数时的3～5圈环索，这是因为第1～2内圈索撑节点因相邻索段间夹角较小导致索撑节点处滑移摩擦力增加，节点预应力损失较大分别达到20.50%、15.19%；第3～5圈环索由于索撑节点相邻索段间夹角逐渐增大且张拉点数增加，节点预应力损失较小分别为6.58%、3.98%和4.88%.4)摩擦因数取0.03时索撑节点平均预应力损失五圈环索比较接近最大仅为1.07%，表明当钢夹片和索体间没有相对滑移时，索撑节点相邻索段间夹角及张拉点数量对节点预应力损失影响不大.

3.3 屋盖撑杆和拉杆应力

屋盖撑杆和拉杆最大应力随施工步的变化曲线如图8所示.因索撑节点取不同摩擦因数时屋盖撑杆、拉杆应力分布规律基本一致，限于篇幅仅列出摩擦因数取0.3的屋盖张拉完成时撑杆和拉杆应力云图(图9).

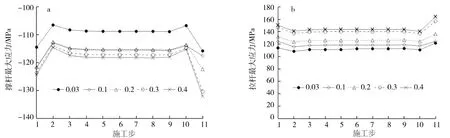
a.撑杆最大应力; b.拉杆最大应力.图8 屋盖撑杆和拉杆最大应力变化曲线Fig.8 Maximum stress curves of roof strut and tention members

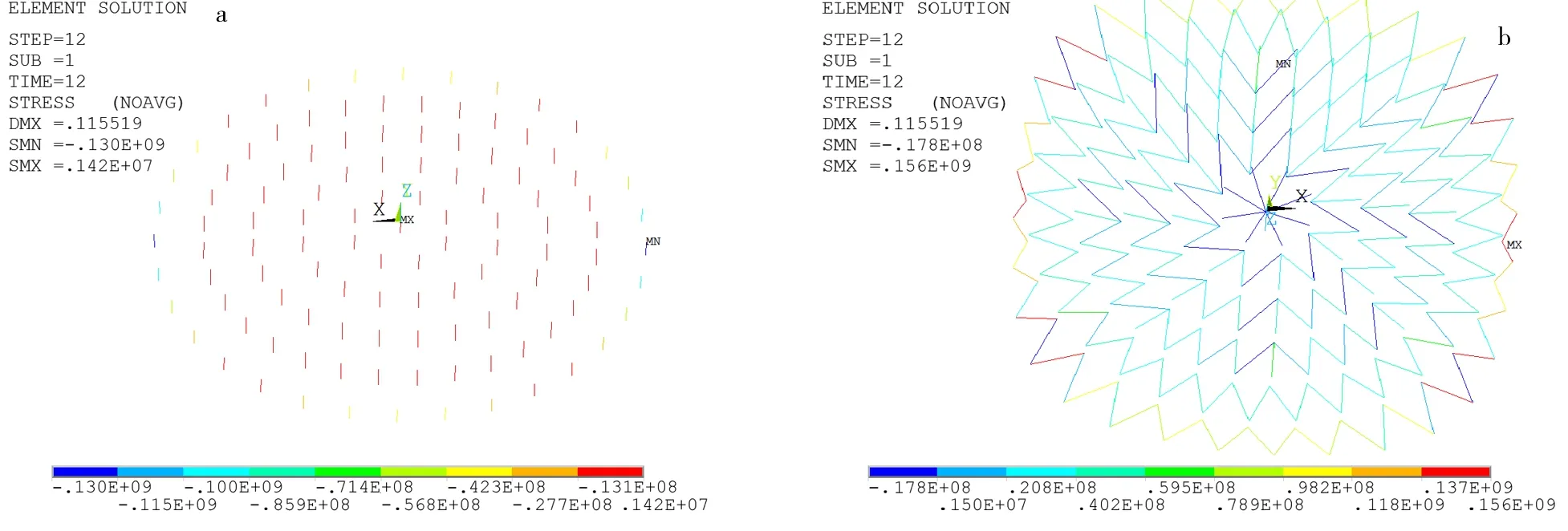
图中应力单位Pa a.撑杆应力 b.拉杆应力.图9 屋盖撑杆和拉杆应力云图(摩擦因数0.3)Fig.9 Stress nephogram of roof structure’s struts and tention members (friction coefficient 0.3)

由图8和图9可见：1)屋盖撑杆和拉杆最大应力在整个张拉过程中均未超过其材料的屈服强度，满足设计要求. 2)撑杆和拉杆最大应力随摩擦因数增加均呈逐渐增大趋势，表明因索撑节点摩擦所造成的预应力损失越大环索超张拉幅度越大，导致撑杆和拉杆应力也随之增加.3)当张拉最外圈环索(第1、11施工步)时撑杆和拉杆最大应力均大于其他施工步，而第2～10施工步过程中，两者最大应力几乎不变，表明内圈环索的张拉对撑杆和拉杆最大应力影响很小，张拉最外圈环索是屋盖撑杆和拉杆受力最大的控制施工步，施工时应对该区域杆件进行安全监测，此外撑杆和拉杆应力突变对索撑节点处带来的位移变化也应重点监测，这将影响结构成形后的撑杆垂度，对后期结构稳定造成不利影响.4)撑杆和拉杆应力以屋盖长轴、短轴为对称轴呈对称分布模式，其应力最大值均分布在短轴两侧的支座附近杆件，图9b拉杆应力最小值为负值说明在内圈位置中有部分拉杆出现受压情况，但压应力很小，仅为-17.8 MPa.

3.4 屋盖网壳位移

环索张拉完成时，上部网壳下凹和上凸最大位移与索撑节点取不同摩擦因数的关系如图10所示.根据有限元模拟结果，屋盖张拉完成索撑节点取不同摩擦时网壳竖向位移分布规律基本一致，本文以实际工程中索撑节点常用的摩擦因数0.3为例，网壳竖向位移云图如图11所示，图11中位移单位m.

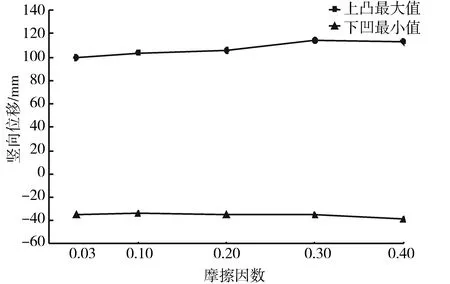
图10 不同摩擦因数下网壳竖向位移曲线Fig.10 Vertical displacement curve of reticulated shell with different friction coefficients

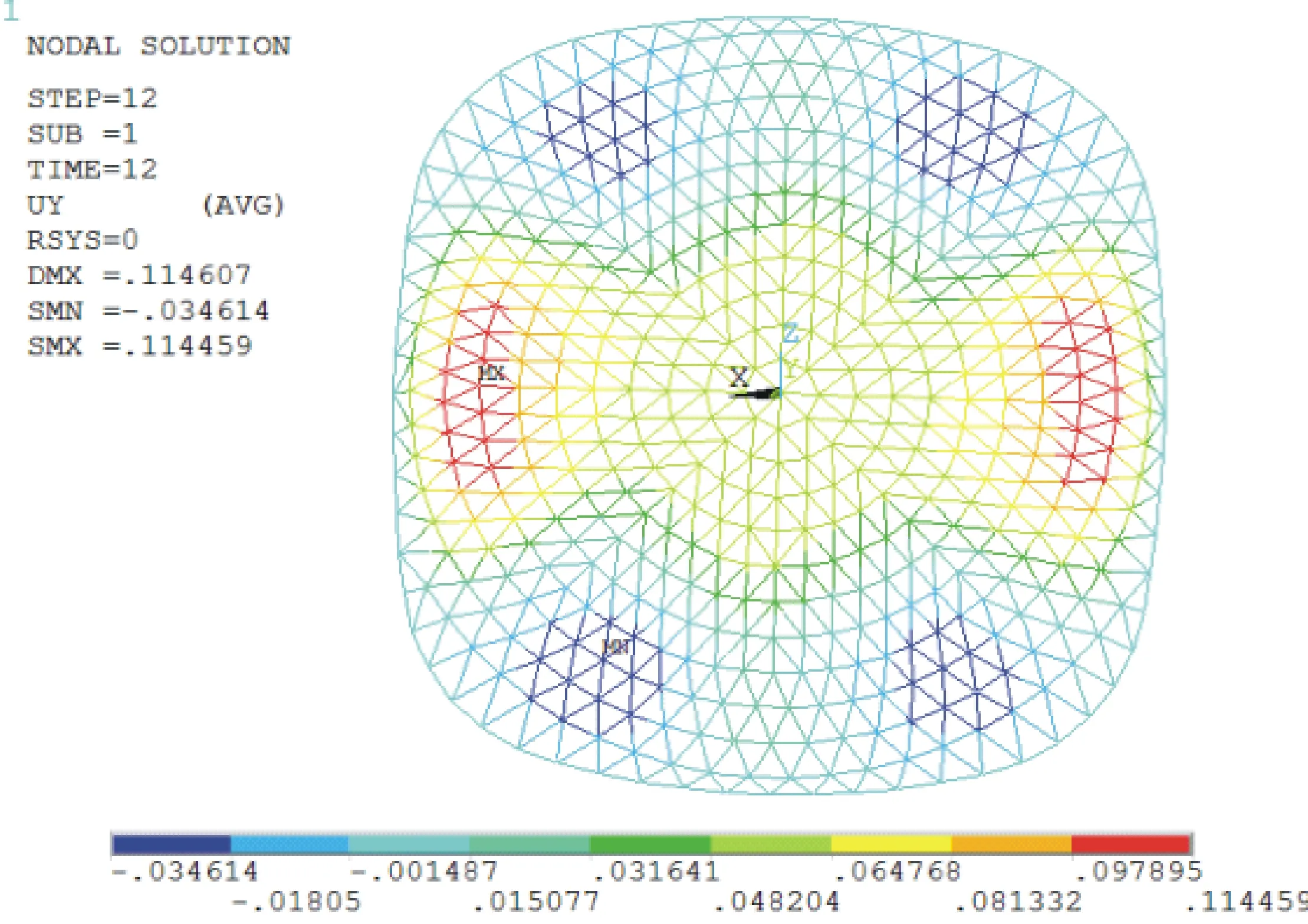
图11 网壳位移云图(摩擦因数0.3)Fig.11 Displacement nephogram of latticed shell(friction coefficient 0.3)

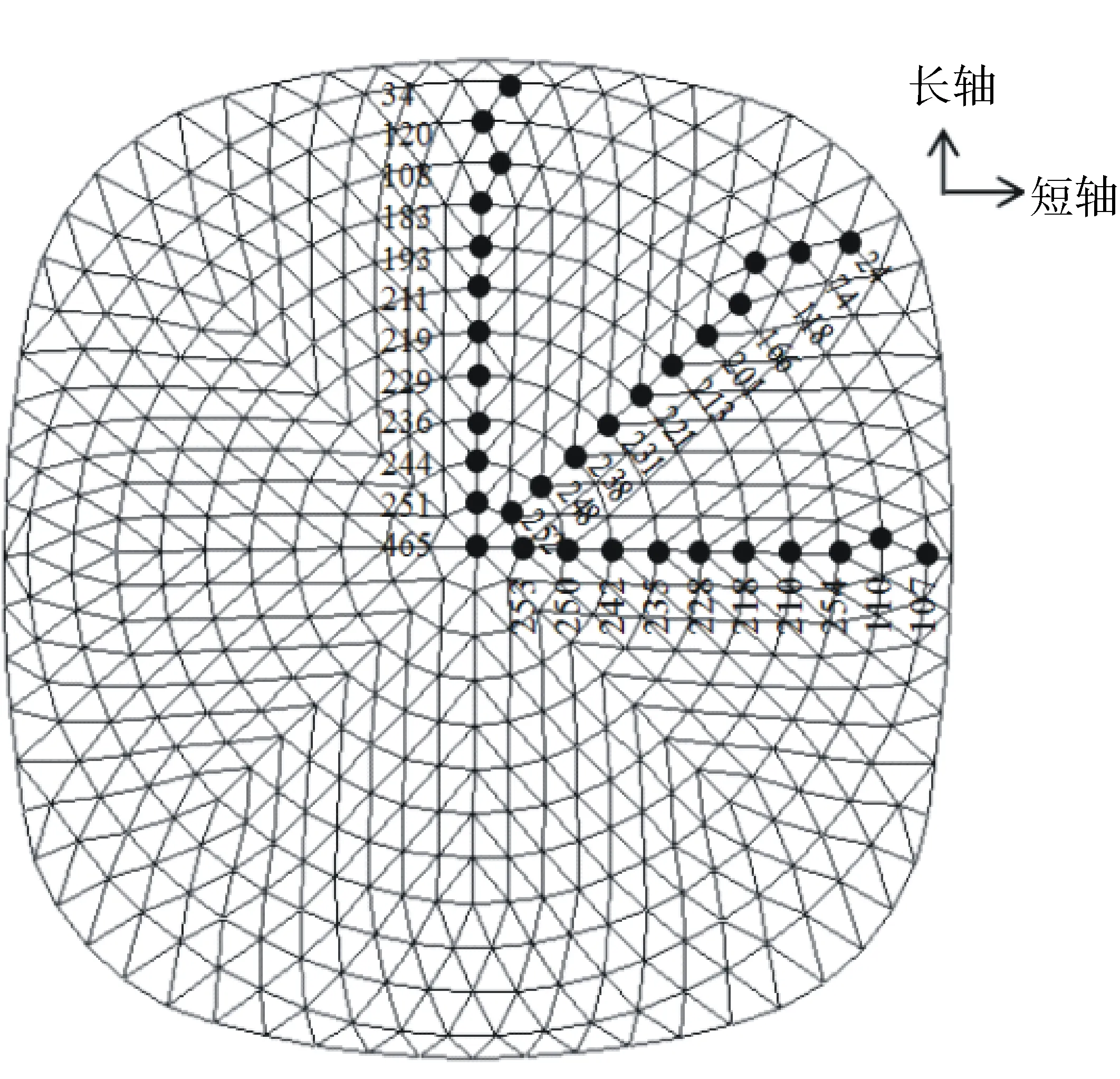
图12 网壳节点号Fig.12 Shell node number

由图10可见：1)网壳下凹最大位移随索撑节点摩擦因数的增大呈增大趋势但增幅很小，摩擦因数由0.03增至0.4网壳下凹最大位移仅增加5 mm；2)当摩擦因数由0.03增至0.3时网壳上凸最大位移呈逐渐增大趋势，但增幅也很小仅14 mm(为短轴跨度的1/598 3)，摩擦因数取0.3和0.4时网壳上凸最大位移2者相近；3)由以上分析可知索撑节点摩擦因数的取值大小对上部网壳下凹和上凸最大位移影响很小.

由图11可看出：1)网壳竖向位移以屋盖长轴、短轴为对称轴呈对称分布模式.2)最大竖向上凸位移分布于网壳短轴端部第4圈环索周围的局部网壳节点，最大竖向下凹位移分布在与长轴、短轴基本均呈45°方向、第4～5圈环索间网壳局部节点.3)网壳竖向位移值在同圈环向方向变化趋势：网壳中心至第3圈环索间上凸且分布均匀，第4～5圈环索间由短轴端部的上凸逐渐降为沿45°方向的下凹再逐渐增至长轴端部的上凸状态.

因屋盖网壳起拱情况是环索张拉施工的重要研究内容，为便于分析网壳起拱规律，并使分析结果具有一定代表性，根据对称性取上部单层网壳按长轴、短轴方向及与其呈45°方向的关键节点[16]进行标记，如图12所示.本文仍以实际工程中索撑节点常用的摩擦因数0.3为例，研究上部网壳节点竖向位移在张拉全过程中的变化情况，见图13.

由图13可得出：1)第1批由外至内张拉环索阶段，沿长轴和45°方向的网壳节点竖向位移变化规律相近，在张拉某圈环索时其对应的网壳节点位移较前一个施工步增幅明显加大，且已张拉完成的网壳节点位移随着由外向内环索张拉而逐渐回落，致使网壳节点位移由外至内呈“波浪式”推进发展.沿短轴方向杆件因传力路径短使得其网壳节点位移发展与上述2者不同，第4、5圈环索张拉时，其所对应上部网壳节点竖向上凸位移最大，随着环索张拉向内圈进行，内圈对应上部网壳节点平稳起拱，外圈节点竖向位移回落较小.2)胎架卸载，屋盖结构失去临时支撑后竖向刚度降低导致整体网壳节点位移回落，但因屋盖施工时存在较强的几何非线性致使整体网壳下降幅度不同，沿长轴和45°方向分别在对应第4圈环索的上部网壳183号节点和第4、5圈环索间的上部网壳118号节点处呈现“凹陷”状态，这2个部位因上部网壳传力路径长，造成顶升效果不足以支持落架后外围更大网格所带来的自重因而形成凹陷；而沿短轴方向网壳因杆件传力路线短节点基本均下降7 mm左右.3)第2批由内至外张拉环索阶段，网壳竖向节点位移曲线形状基本不再变化，其随施工步进行逐渐缓慢增大.张拉结束时网壳竖向节点位移，沿长、短轴方向均处于上凸状态，沿45°方向在支座至第3圈环索间呈下凹状态.4)在全过程张拉施工中，周边支座至第3圈环索间对应网壳起拱的变化较大并出现不均匀上凸和下凹情况，故在实际施工过程中最外两圈环索的张拉造成的网壳变形应是重点监测部位.

a.第1批张拉及胎架卸载(长轴方向);b.第1批张拉及胎架卸载(短轴方向)；c.第2批张拉及胎架卸载(长轴方向); d.第2批张拉及胎架卸载(短轴方向)；e.第1批张拉(45°方向); f.第2批张拉(45°方向).图13 张拉过程中的竖向位移Fig.13 Vertical displacement curves of reticulated shell during tensioning

4 结论

通过对河北北方学院体育馆弦支穹顶屋盖考虑索撑节点摩擦的预应力施工模拟分析，可得如下结论:

1)各圈环索预应力随索撑节点摩擦因数增大在对应施工步逐渐增大，屋盖结构张拉全过程中取5种不同摩擦因数时各圈环索预应力变化趋势基本一致.当各圈环索最低预应力均值达到预应力设计值时，随索撑节点摩擦因数增大，环索最高预应力均值、预应力偏差以及索撑节点平均预应力损失都不断增大.

2)本文结构屋盖第1～2圈环索因相邻索段间夹角较小使得索撑节点处滑移摩擦力增加，导致节点平均预应力损失均大于取相同摩擦因数时的3～5圈环索.屋盖张拉阶段因相邻圈环索张拉施工时相互影响明显，所有环索会在张拉时出现新的动态内力平衡状态，故对环索预应力要作较为精确地控制，且张拉施工时应持续监测环索预应力变化.

3)下部索撑体系的撑杆和拉杆应力以屋盖长轴、短轴为对称轴呈对称分布模式，两者最大应力随摩擦因数增加均呈逐渐增大趋势且皆出现在短轴两端，施工时应对该区域杆件进行安全监测.张拉最外圈环索是屋盖撑杆和拉杆受力最大的控制施工步，张拉内圈环索对其影响很小.

4)索撑节点摩擦因数取值大小不影响上部网壳竖向位移分布规律，且对网壳下凹和上凸最大位移值影响很小.本文屋盖上部网壳采用类圆角矩形拓扑结构导致网壳节点竖向位移在张拉过程中，第3圈环索以内沿环向和径向上凸且呈均匀对称发展，周边支座至第3圈环索区域的网壳节点位移由长轴、短轴两端上凸向45°方向逐渐凹陷.短轴两端因传力路径短所获竖向位移较大，但过大的位移值会在后期找形过程中带来困难.