具有弱Allee效应的捕食-食饵模型的向量场分析
关 宁,赵立纯,*,刘敬娜
(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
在种群生态系统中,种群的繁衍生存不能缺少营养,食物链和食物网构成了种群间的营养关系,这就是种群间的捕食现象.捕食-食饵之间的相互作用是生态学中最基本的种间关系,同时也是生物链及整个生态系统建立的基础,因此,对捕食-食饵模型的分析在生物数学研究中是非常重要的课题[1].对于一个具有弱Allee效应的种群,当其种群密度过于稀疏时,它的出生率会减少,种群密度增速慢,但始终不会出现负出生率的情况[2].
常微分方程是通过数学方法解决生产生活中实际问题的重要工具,向量场是研究常微分方程定性分析的重要手段[3]并在许多领域得到应用.在工程方面,罗健根据Lyapunov导航向量场的导航法则,研究多架无人机协同跟踪问题,成功实现了跟踪任务[4];在动力学领域,寇力英等人通过引入并完善大尺寸分块矩阵的新记号表示方法,研究一类具有对称性质的四维幂零向量场的超规范形问题,最终简化了繁琐的大尺寸矩阵运算,获得一种新方法[5];在物理学中,Emanuele Paolini等人将微分方程向量场推广到度量空间,并成功应用于速度场的描述中[6];在生物学中,基于疟疾传播SEIR模型,殷红燕等人利用向量场以及定性分析的理论对不育蚊子进行研究,得出结论:不育蚊子释放有利于控制蚊子导致的疾病传播[3].基于此,本文进一步将向量场理论应用于具有弱Allee效应的捕食-食饵模型的研究中.
1 模型建立
考虑具有弱Allee效应的Logistic模型[7]
(1)
其中,x为食饵种群密度,ε为种群的内禀增长率,K为其环境容纳量.
(2)
用以下时滞模型表示捕食者种群对食饵种群的影响:
(3)
其中,a>0为时滞参数,ω为捕食者种群对食饵种群的影响系数.
(4)
其中,y为捕食者种群密度.
结合模型(3)(4)有
(5)
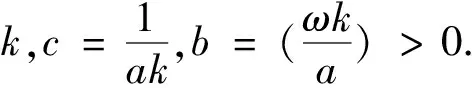
将u记为t,得到本文的主要模型
(6)
先对模型(6)进行定性分析,然后再利用Mathematica软件绘制向量场图,以刻画种群之间的相互作用[8],最终根据平衡点周围向量场的走向对模型进行生物解释.
2 模型分析
对模型(6),令
得模型平衡点为:P0=P1=(0,0),P2=(k-b,k-b).
定理1对模型(6),若k=b,则模型有唯一平衡点P0,并且其为稳定结点.
证明当k=b时,易解得模型(6)有唯一平衡点P0.
对于平衡点P0(0,0),模型(6)相应的Jacobian矩阵为
相应的特征方程为
λ2-T1λ+D1=0,
(7)
其中,T1=-1,D1=0.
由于D1=0,平衡点P0(0,0)是模型(6)的高阶奇点,根据文献[9],对高阶奇点的性态分析得出平衡点P0为稳定结点.
定理2对模型(6),若k≠b,则模型有两个平衡点P1=(0,0)和P2=(k-b,k-b),
(1)平衡点P1是鞍结点.

证明当k≠b时,易解得模型(6)有两个平衡点P1和P2.
对于平衡点P1(0,0),同理可知其为模型(6)的高阶奇点,根据文献[10]中对高阶奇点的性态分析得出平衡点P1为鞍结点.
对于平衡点P2(k-b,k-b),模型(6)相应的Jacobian矩阵为
相应的特征方程为
λ2-T2λ+D2=0,
(8)
特征根为
其中,T2=c(k-b)(2b-k)-1,D2=c(k-b)2>0.
随后将定理1、定理2的结论分别用微分方程向量场的形式表出.
3 向量场分析
3.1 一个平衡点
对定理1,取k=b=10,c=0.1,得图1.从图1可以看出:P0是稳定结点,根据生物含义有x≥0,y≥0,即区域Ⅰ部分,而P0=(0,0)表示捕食者种群和食饵种群都处于灭绝状态.
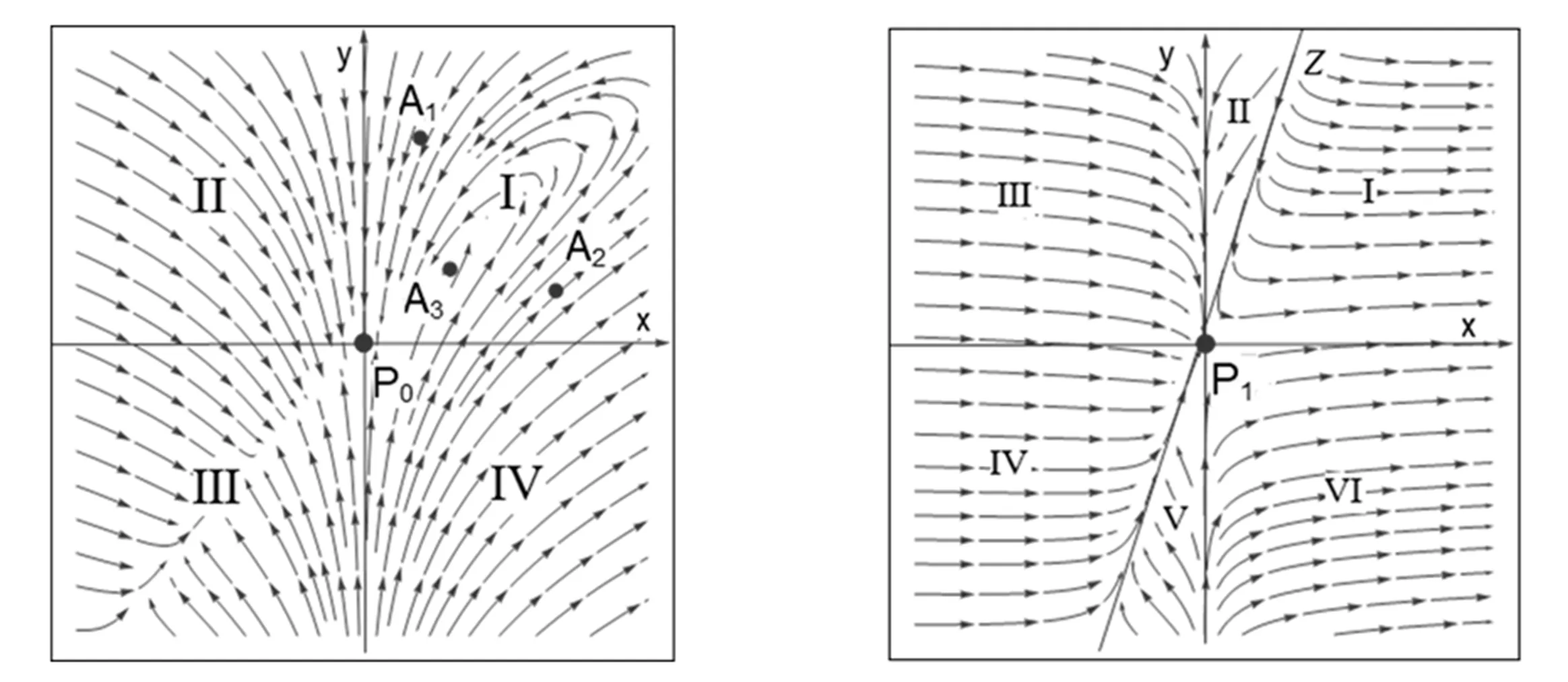
图1 模型(6)在平衡点P0附近的向量场图 图2 模型(6)在平衡点P1附近的向量场图
从图形的向量场可以看出,两种群的变化趋势有以下几种情况:
情况1如果种群的初始状态落在点A1的位置,随着时间的推移,两种群都会走向灭绝;
情况2如果种群的初始状态落在点A2或A3的位置,随着时间的推移,两种群数量先增加然后减少,最后到达灭绝状态.
3.2 两个平衡点
对平衡点P1=(0,0),取k=150,b=50,c=0.1,得图2.从图2可以看出:P1是鞍结点,根据生物含义有x≥0,y≥0,即区域Ⅰ、区域Ⅱ部分,并且P1=(0,0)表示捕食者种群和食饵种群都是灭绝状态.
从图形的向量场可以看出,两种群的变化趋势有以下几种情况:
情况1如果种群的初始状态落在Ⅰ区域的位置,随着时间的推移,捕食种群的数量减少,则食饵种群的数量会增加;
情况2如果种群的初始状态落在Ⅱ区域的位置,随着时间的推移,两种群数量都会减少,最后到达灭绝状态.
对平衡点P2=(k-b,k-b),取k=100,c=0.01,则b=51.02,得图3,其中,P2=(48.98,48.98). 图3中(a)图表示包含平衡点P1与平衡点P2的全局图,(b)图表示在平衡点P2附近的局部图.在图形3(b)中,L表示直线x=48.98,l表示直线y=48.98,它们的交点为P2,且图中4个区域内均有x≥0,y≥0,故初始点在区域Ⅰ、Ⅱ、Ⅲ、Ⅳ时有生物含义.进一步分析得出两种群的变化趋势有以下几种情况:
情况1当初始状态落在区域Ⅰ时,随着捕食者种群数量增加,导致食饵种群数量减少;当食饵种群减少到一定程度时,捕食者种群没有足够的生存资源,进而使捕食者种群的数量随之减少(见图3(b)区域Ⅱ);当捕食者种群数量减少到一定程度时,食饵种群数量增加(见图3(b)区域Ⅲ);随着食饵种群数量的继续增加,捕食者种群有充足的生存资源,从而导致捕食者种群数量增加(见图3(b)区域Ⅳ).如此反复进行,使系统处于一种生态平衡状态.
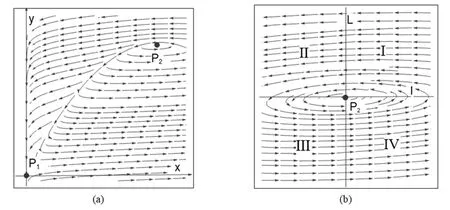
图3 模型(6)在平衡点P2附近的向量场图
情况2当初始状态落在区域Ⅱ、Ⅲ、Ⅳ时,随着时间的推移,两种群数量的变化趋势如同情况1,最终使系统处于一种生态平衡状态.
总之,常微分向量场可以直观刻画种群间的相互作用关系,为理解种群动态的生态学机制提供参考.

