四轮转向系统模糊PID 控制研究

王欲进，谢纯禄，范 英，晋民杰

（1.太原学院机械与电气工程系，山西 太原 030032；2.中铁三局运输工程分公司，山西 晋中 030600；3.太原科技大学交通与物流学院，山西 太原 030024）

1 引言

四轮转向控制技术（4WS）的诞生极大地提升了汽车的操纵稳定性和安全性。很好的改善了传统汽车低速转向灵活性差，高速转向稳定性差等缺点[1]。文献[2]基于模糊控制理论，设计了4WS 模糊控制器，并利用联合仿真验证了控制器得有效性。文献[3]基于4WS 二自由度模型，设计了一种低速比例控制，高速模糊控制的综合控制器，经仿真验证，很好的提高了汽车的操纵稳定性。文献[4]结合前馈控制和模糊控制建立新的控制策略，经联合仿真验证，很大程度改善了汽车的操纵稳定性。以上的研究很好的证明了四轮转向系统的优越性，但从控制效果来看还未达到理想值。基于三自由度非线性4WS模型，设计了模糊PID 控制器，并与前轮转向汽车和比例控制下的4WS 汽车进行仿真对比分析，验证控制器对4WS 汽车的控制效果。

2 4WS 模型的搭建

2.1 三自由度模型

在传统二自由度模型基础上考虑车身侧倾，建立4WS 三自由度模型，简图如图1 所示。

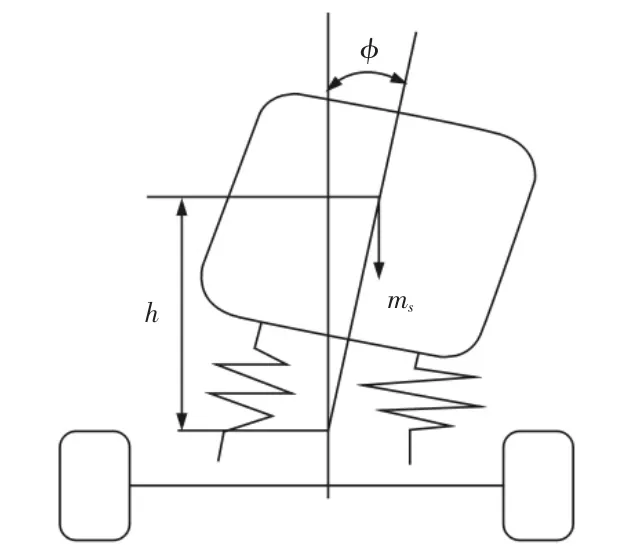
图1 三自由度模型Fig.1 Three-Degree-of-Freedom Vehicle Model

假设汽车纵向速度恒定不变、轮胎侧偏特性呈线性且前后轮小转角情况下，则三自由度模型的动力学方程为：

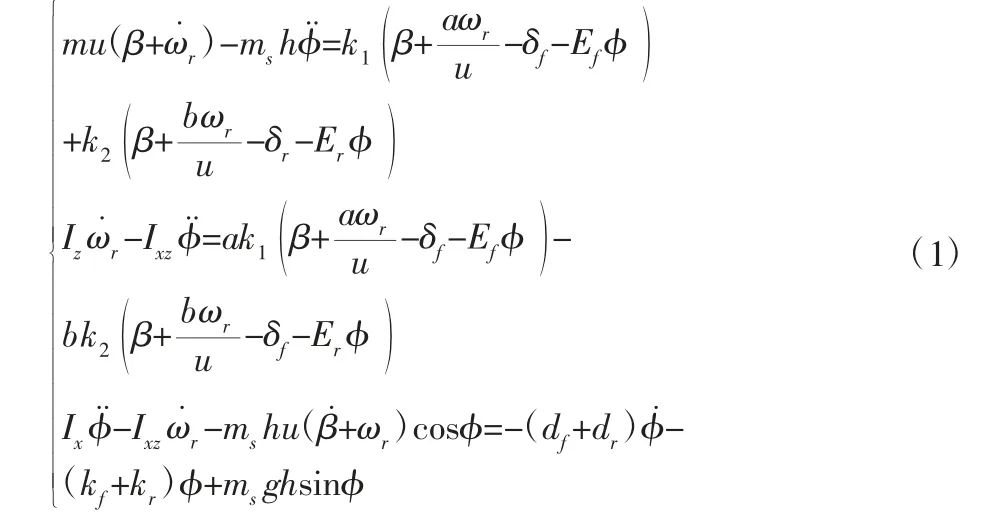
式中：m—整车质量；ms—汽车簧载质量；δf、δr—汽车前、后轮转角；a、b—质心至前后轴距离；u—车身纵向速度；β—质心处侧偏角；h—簧载质心到侧倾轴的距离；φ—车身侧倾角；ωr—横摆角速度；Ix—簧载绕侧倾轴的转动惯量；Iz—车身横摆转动惯量；Ixz—簧载的惯量积。将其化为状态方程，可得：

当δr=0 时，即为前轮转向系统。

2.2 轮胎模型

轮胎是车辆不可或缺的一部分，其力学特性一直是研究的一个重点[5]。且轮胎很大程度上决定了整车的动力学特性，在操纵稳定性和安全性等方面都有很重要的影响。因此，采用魔术公式轮胎模型进行模型的搭建[6]，其形式如下：

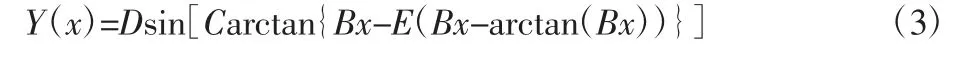
式中：Y（x）—侧向力、纵向力或回正力矩；x—相应的侧偏角或纵向滑移率；B、C、D 依次由轮胎的垂直载荷和外倾角来确定。

根据魔术公式在Simulink 中搭建轮胎的侧向力学模型，如图2 所示。由上述模型可得到轮胎的侧向力学特性，如图3 所示。由图3 可知，当侧偏角在4°以内时，轮胎的侧偏特性呈线性关系，随着侧偏角越来越大，斜率逐渐变小，直至为零。此时，侧偏力达到一个稳定值。

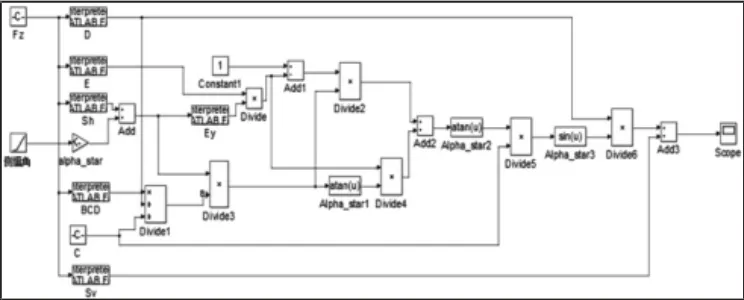
图2 魔术公式轮胎模型Fig.2 Magic Formula Tire Model

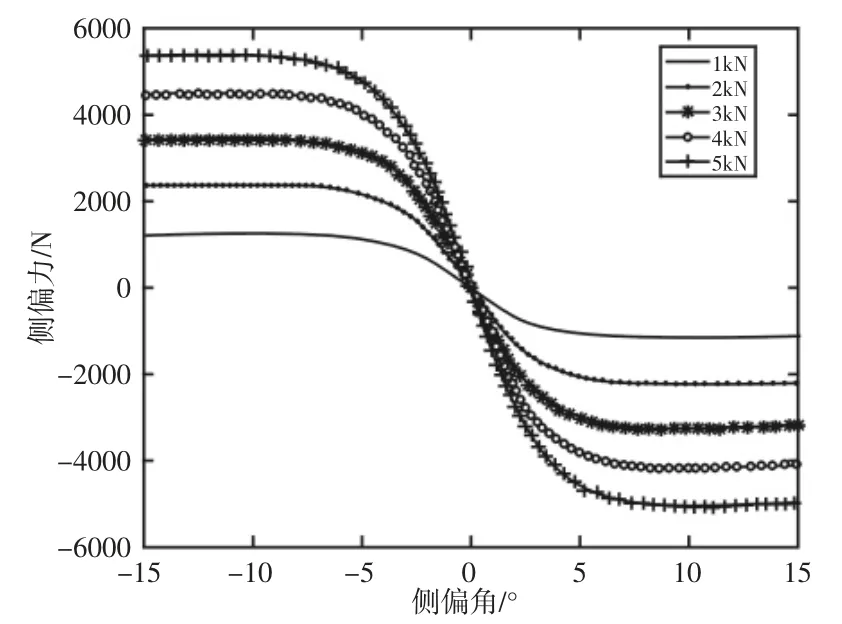
图3 魔术公式轮胎侧向力学特性Fig.3 Magic Formula Tire Lateral Mechanical Properties

2.3 三自由度4WS 非线性模型

四轮转向车辆是相对较复杂的非线性系统，其非线性主要体现在轮胎上[7]，所以模型的建立共分为轮胎模块和车辆模块。结合之前建立的三自由度模型和轮胎模型，搭建三自由度非线性模型，如图4 所示。

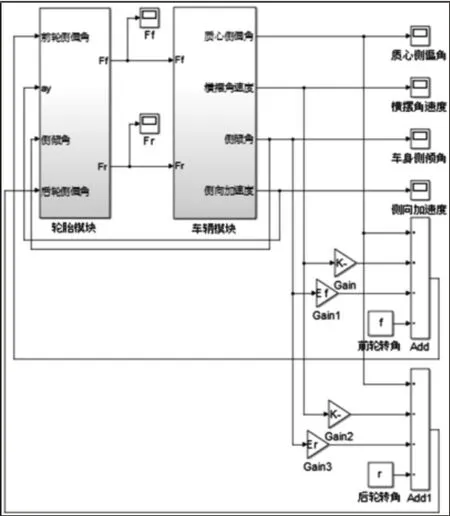
图4 四轮转向汽车三自由度非线性模型Fig.4 Three-Degree-of-Freedom Nonlinear Model for 4WS Vehicles

3 控制器设计

控制方法在汽车运行过程中起着至关重要的作用，他决定了汽车的运动方式，关系到汽车能否高质量的完成既定的任务[8]。由于传统的模糊控制精度较差，所以为了达到预期的控制效果，本章结合模糊理论和PID 控制算法搭建模糊PID 控制器。

模糊控制器是模糊控制系统中的核心所在。结构图，如图5所示。

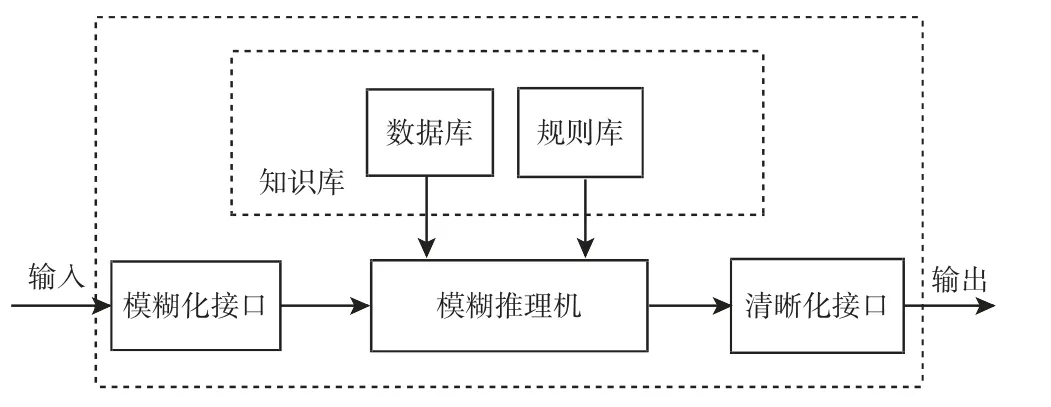
图5 模糊控制器结构图Fig.5 Fuzzy Controller Structure

在控制领域中，PID 控制算法因其结构简单、稳定性好等优点被广泛应用，其控制原理，如图6 所示。

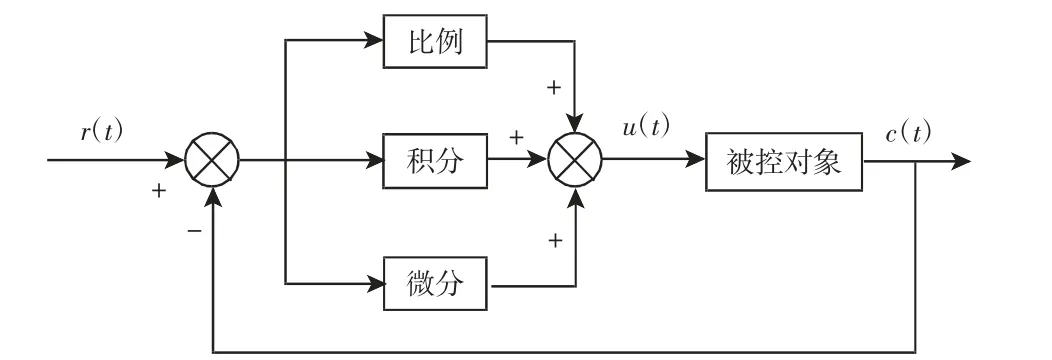
图6 PID 控制器原理图Fig.6 PID Controller Schematic

模糊PID 控制器是模糊控制与PID 控制的结合，兼备两种控制的优点，并且可根据实际情况对参数进行调整。选择两输入类型，利用模糊规则库对PID 的参数进行修改调整。控制原理图，如图7 所示。

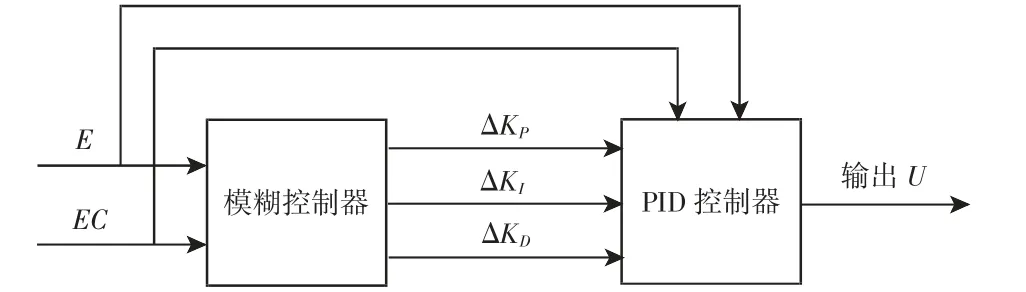
图7 模糊PID 控制器原理图Fig.7 Fuzzy PID Controller Schematic

由图7 可知，将系统的误差及其变化率E、EC 作为模糊控制器的输入，找出ΔKP、ΔKI、ΔKD与E 和EC 之间的模糊关系，并不断地对其进行修改调整，以满足控制的需要。其中系统误差E 和误差变化率EC 的模糊子集均为｛NB，NM，NS，ZO，PS，PM，PB｝，设置E 和EC 的论域为［-3，3］，ΔKP、ΔKI、ΔKD的论域为［-1，1］。分别将高斯函数和三角函数作为输入、输出隶属度函数，如图8所示。模糊控制规则基于专家经验知识，并对被控对象的属性进行反复试验分析和归纳总结，从而得到模糊控制规则。在确定了隶属度函数及模糊控制规则后，需要对控制器的输出进行解模糊处理，最终可得到ΔKP、ΔKI、ΔKD的精确值。采用Mamdani 法进行模糊推理，并利用重心法[9]进行解模糊处理。解模糊化后得到ΔKP、ΔKI、ΔKD的曲面图，如图9 所示。

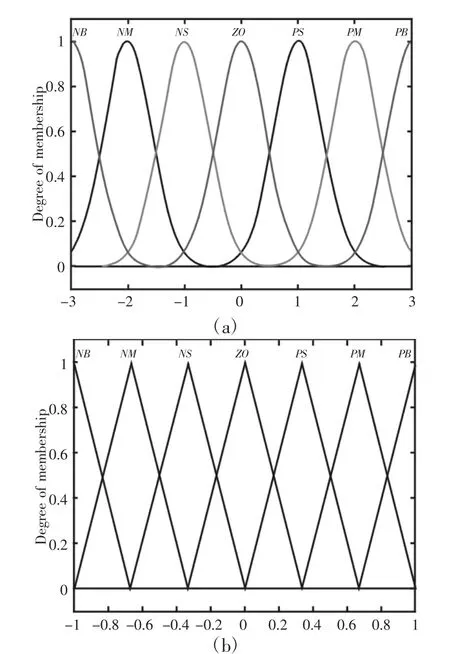
图8 输入输出变量隶属度函数Fig.8 Input/Output Variable Membership Function

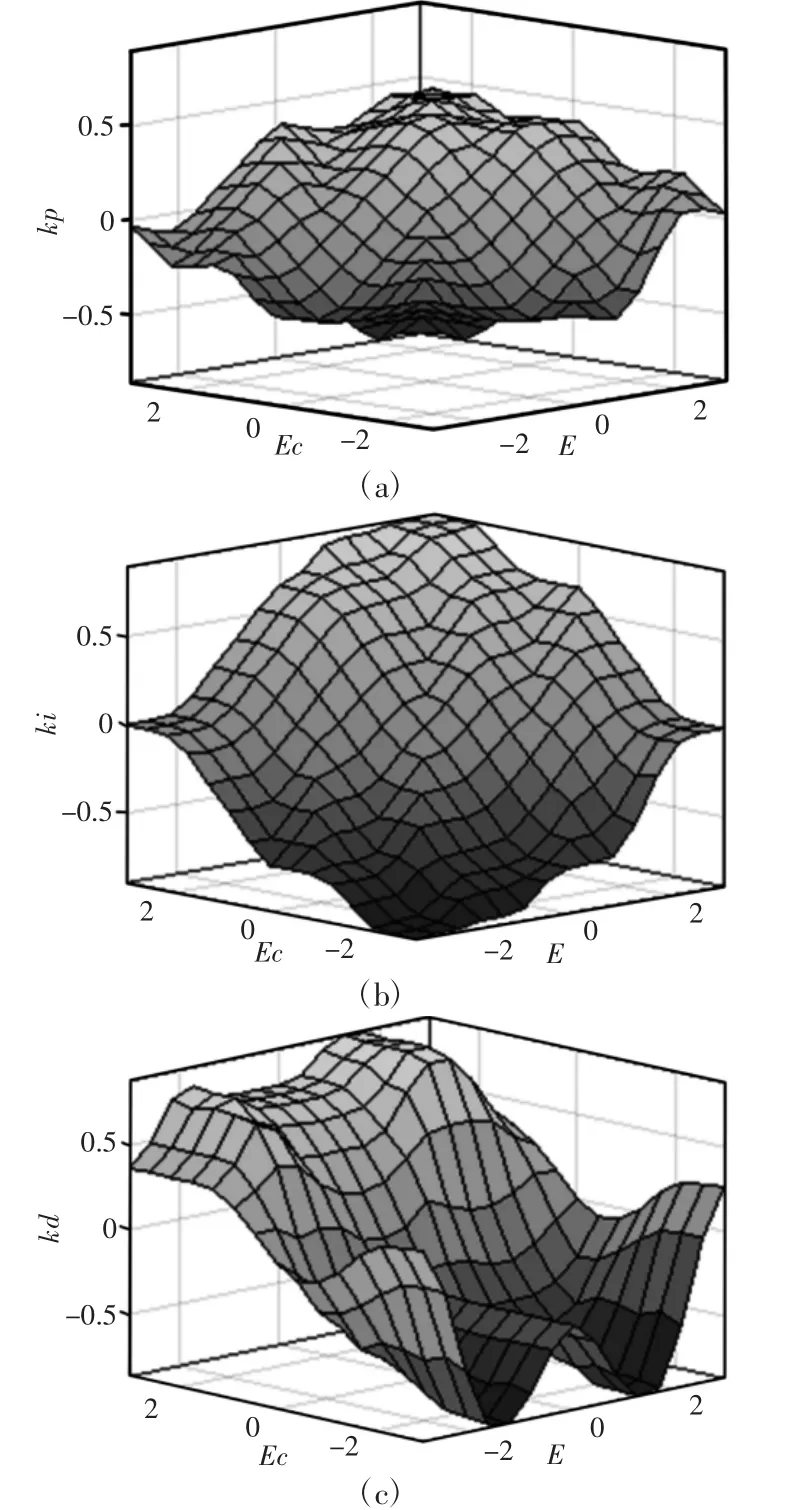
图9 ΔKP、ΔKI、ΔKD 输出曲面Fig.9 ΔKP、ΔKI、ΔKD Output Surface

基于上述得到的隶属度函数、模糊控制规则以及推理机制，在Simulink 中的Fuzzy Logic Tool box 模块建立模糊PID 控制器模型，如图10 所示。基于模糊PID 控制器模型，搭建整车仿真模型，如图11 所示。

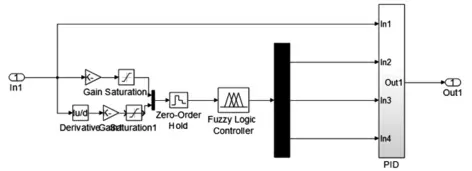
图10 模糊PID 控制器模型Fig.10 Fuzzy PID Controller Model

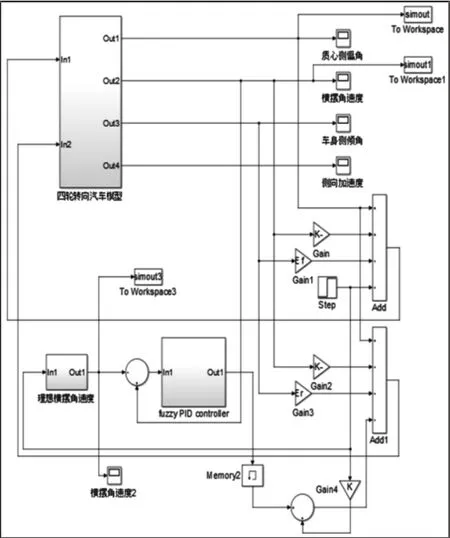
图11 四轮转向模糊PID 综合控制模型Fig.11 Four-Wheel Steering Fuzzy PID Control Model

4 仿真对比分析

取前轮转角输入为0.1rad，起跃时间为0.1s。车速分别为5m/s 和20m/s，在模糊PID 控制器的基础上增加前轮转向控制器和比例控制器的对比，仿真分析各个控制器在低速和高速情况下对车辆的控制效果。仿真结果，如图12、图13 所示。由图12可知，相较于传统前轮转向汽车，4WS 汽车的稳态质心侧偏角明显降低，增强了汽车的低速机动性和高速稳定性。其中在低速时比例控制下的质心侧偏角较低，而高速时模糊PID 控制下的质心侧偏角更加接近于零，很好的提升了汽车高速行驶的稳定性。

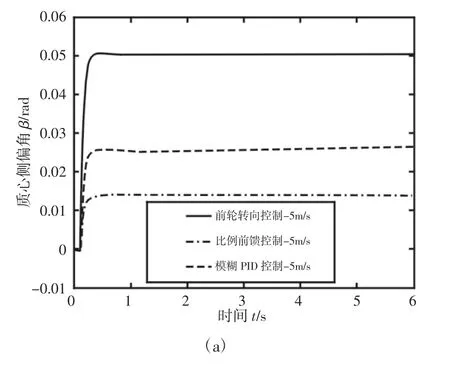
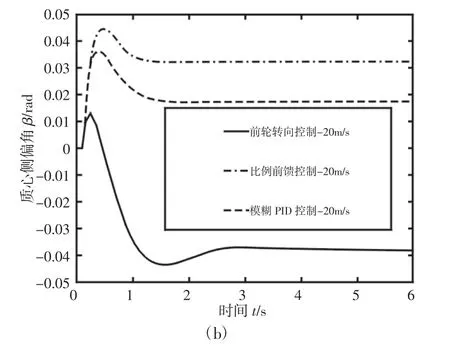
图12 质心侧偏角响应Fig.12 Core-of-Mass Side-Slip Response

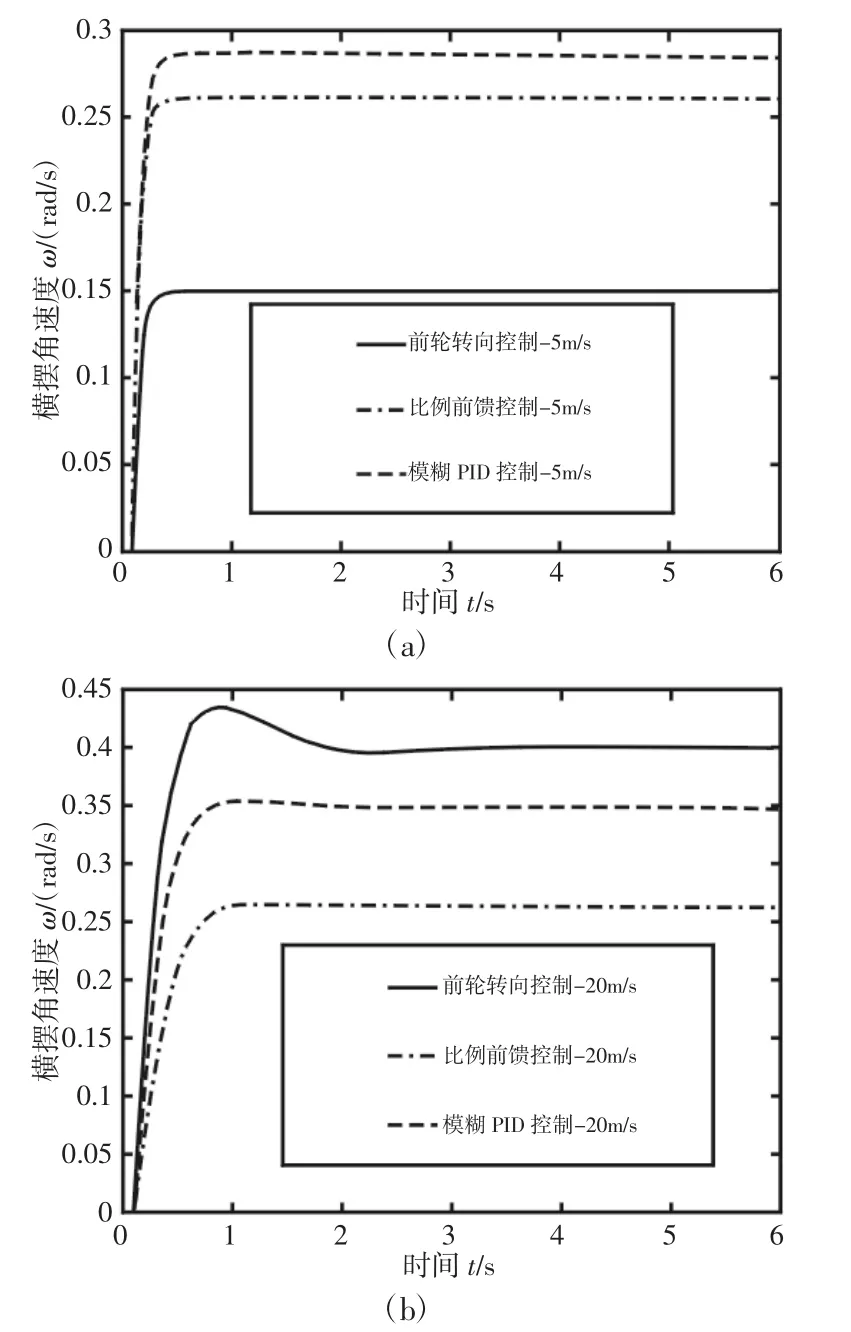
图13 横摆角速度响应Fig.13 Yaw Angular Velocity Response

由图13 可知，在低速时，4WS 汽车横摆角速度比前轮转向控制的汽车略微增大，提高了汽车的机动灵活性。其中，模糊PID控制的横摆角速度上升幅度更大，大幅降低了汽车的转弯半径。在高速行驶时，4WS 汽车的横摆角速度略微减小，提高了汽车的稳定性和安全性。其中比例控制下的横摆角速度下降幅度过大，提升了驾驶员驾驶的难度，而模糊PID 控制下的横摆角速度与前轮转向汽车的横摆角速度更加接近，很好地保持了汽车原有的转向感觉。

综上所述，模糊PID 控制可以有效的降低汽车的质心侧偏角，大大地提高了汽车循迹能力和行驶稳定性，且横摆角速度与前轮转向汽车相近，降低了驾驶员驾驶难度。很大程度的提升了汽车的操纵稳定性。

5 结论

（1）在传统二自由度模型基础上，考虑车身侧倾和轮胎非线性特性，建立更加接近实际车辆的三自由度非线性模型。

（2）对阶跃输入下前轮转向控制器、比例控制器和模糊PID控制器的控制效果进行对比分析，结果表明：模糊PID 控制下的4WS 汽车能够使得汽车的质心侧偏角更加接近于零，且横摆角速度与前轮转向汽车相近，可以确保驾驶员能更好的适应四轮转向汽车，控制效果较之前轮转向控制和比例控制更佳，极大地提升了汽车的操纵稳定性。