齿轮箱故障诊断的启动电流阶次分析方法研究
张思敏,任 芳,杨兆建,李 峰
(1.太原理工大学机械工程学院,山西 太原 030024;2.煤矿综采装备山西省重点实验室,山西 太原 030024)
1 引言
齿轮箱作为调节转速和传递扭矩的常用旋转机械设备,在工业生产中得到了广泛的应用,齿轮箱是否正常运行将直接决定机械设备能否进行正常工作[1]。因此,实现齿轮的早期故障诊断具有重大意义。在实际生产中,由于存在诸如传感器安装不方便,易受背景噪声的干扰等缺陷,导致传统的振动信号分析法和噪声分析法难以实施[2]。近年来,学者们逐渐将故障诊断的注意力转向基于电气方法的无损诊断技术。
在采用电机驱动的齿轮传动系统中,可直接利用电机本体作为传感器来实现齿轮故障的无损诊断[3]。与传统故障诊断方法相比,驱动齿轮箱的电机电流信号具有信噪比高、信息集成度高、信息获取方便等优点[4]。
电机电流特征分析法(MCSA)通常利用电机稳态电流来进行故障诊断[5-7],但由于故障特征分量较小,加上外界干扰的影响,故障特征分量很容易被湮没,以致在故障诊断时无法准确判断是否存在故障特征分量。而在电机启动过程中,其电流信号包含着更多的故障信息,平稳运行时不易反映出来的故障特征得以充分表现[8-10]。因此,提出了一种电机启动电流特征分析法(Motor Starting Current Signature Analysis,简称MSCSA),将电机启动电流作为故障诊断的切入点,基于对它的阶次分析来实现齿轮的故障诊断。
2 启动电流阶次分析原理
2.1 齿轮故障诊断的电机电流分析
当齿轮出现齿面磨损、断齿等故障时,故障处啮合刚度幅值会迅速下降。以从动齿轮断齿故障为例,断齿每啮合一次,负载转矩便引入一个瞬时冲击,随着齿轮系统的运转,系统会产生附加的波动转矩,为了平衡这个转矩电机会产生一个相应的电磁转矩,从而导致在定子电流中产生非线性的电流信号[11]。因此可以根据电机定子电流频谱中是否出现fe±nfr(fe—电流基频;fr—故障齿轮转率;n=1,2,3…)边频带来对齿轮故障与否做出判断。
2.2 阶次分析方法
阶次分析是通过等角度采样将时域的非平稳信号转换为角度域的平稳信号获得稳定阶次谱的一种分析方法[12],在旋转机械故障诊断研究中起着十分显著的作用。阶次分析技术源于角域采样理论,其关键是实现对原始信号的等角度采样[13]。由于齿轮箱复杂工作环境的限制,使得转速计的安装极不方便,因此拟采用基于瞬时频率估计的无转速计阶次分析方法,如图1 所示。
无转速计阶次分析可分为三个过程:
(1)通过相关系数法获得原始电流信号经EMD 分解后的敏感IMF 分量,并对其进行Hilbert-Huang 变换求解其瞬时频率估计,再利用分段多项式拟合的方式对电机转速进行估算;
(2)根据拟合的转速计算出等角度采样的鉴相时标,然后对原始电流信号进行三次样条插值重采样,从而得到稳态的等角度重采样信号;
(3)对等角度重采样信号进行快速傅里叶变换(FFT),得到阶次谱。
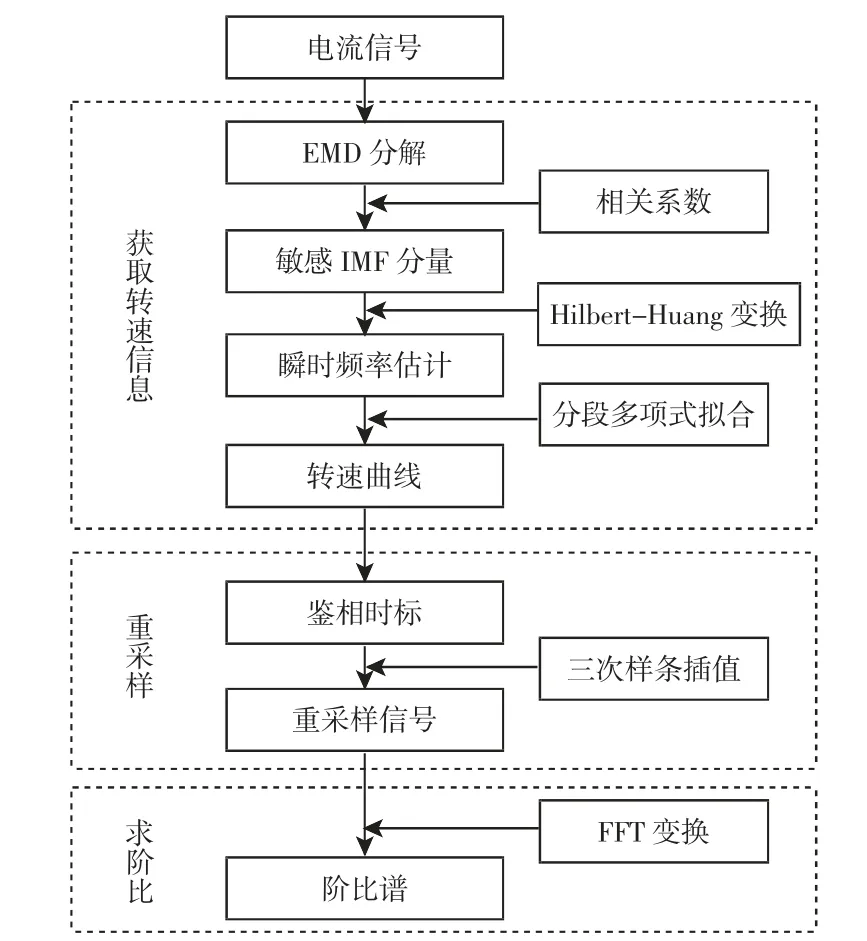
图1 启动电流阶次分析的流程图Fig.1 Flow Chart of Starting Current Order Analysis
2.2.1 敏感IMF 分量选取
相关系数根据以下公式计算:

式中:Ei—数学期望;μi—均值;σi—标准差。
敏感IMF 分量选取原则:在尽可能少地选取IMF 数量的情况下,保证含有齿轮故障有效信息的IMF 不被剔除。
2.2.2 等角度重采样原理
等角度重采样就是把等时间间隔信号转化为等角度间隔信号的过程,求得正确的鉴相时标是进行此转换的必要条件。其步骤如下:
(1)将经Hilbert-Huang 变换后的时频曲线拟合得到转速曲线
式中:a3k、a2k、a1k、a0k—通过分段拟合所得转速曲线函数的多项式系数。
(2)对拟合的转速曲线函数积分,求得等角度采样的鉴相时标,转速曲线与鉴相时标满足式(3)的关系。

式中:Tn—鉴相时标;n—时标序号;T0—该段速度拟合曲线的初始时间;Δθ—等角度采样的采样间隔。
(3)等角度采样和等时间采样的采样点一般不同,所以需要根据所求的鉴相时标Tn对原始采集的启动电流信号进行插值处理,选用三次样条插值方法对等角度采样信号进行插值运算。
值得注意的是,角域采样必须满足采样定理,角域信号的奈奎斯特采样定理,如式(4)所示。

式中:Os—数据的阶次采样率;Omax—分析信号中的最大阶次。等角度采样中,采样阶次等于采样角度间隔的倒数,即Os=1/Δθ。
3 仿真信号的阶次分析
参考电机启动电流理论模拟信号,构建多分量非线性调频信号如下:
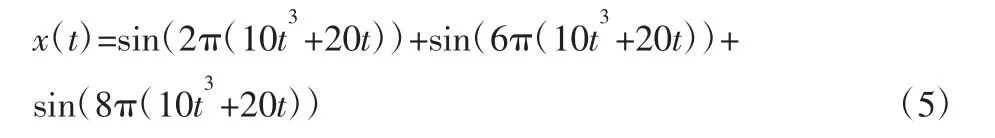
对式(5)所列信号进行仿真分析,其中采样频率fs=1024Hz,采样点数N=1024,仿真信号的基频f1=30t2+20。由仿真信号表达式可知,该信号分量的阶次分别为1、3、4,所以令最大阶次Dmax=10。绘制仿真信号x(t)的时域波形图和经快速傅里叶变换后的幅频特性曲线,如图2、图3 所示。

图2 x(t)的时域波形Fig.2 Time-Domain Waveform of x(t)

图3 x(t)的幅频谱Fig.3 Spectrum of x(t)
由图2 可知,仿真信号x(t)的频率在采样时间内是逐渐增加的,但图3 中的幅频特性曲线存在明显的“频率模糊”现象,无法对信号进行有效地分析。由此可见传统频谱分析方法不适用于分析非稳态信号。
对仿真信号x(t)进行EMD 分解,经EMD 自适应分解后得到了6 个IMF 分量和一个残余分量res,如图4 所示。
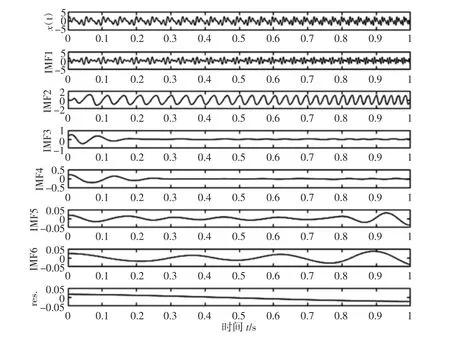
图4 x(t)经EMD 分解结果Fig.4 The EMD Decomposition Results of x(t)
求取EMD 分解后的各IMF 分量与仿真信号x(t)的相关系数,其结果,如表1 所示。可以看出IMF1 分量与仿真信号x(t)的相关性最大,因此IMF1 分量为敏感IMF 分量,将选取IMF1 分量的瞬时频率作为仿真信号的基频成分。

表1 各IMF 分量与x(t)的相关系数Tab.1 The Correlation Coefficient of Each IMF with x(t)
对IMF1 分量进行Hilbert-Huang 变换求得的瞬时频率估计,如图5 所示。对所求得的瞬时频率通过分段多项式拟合的方式对仿真信号x(t)的时频曲线进行拟合,如图6 所示。利用转速和频率的关系获得仿真信号x(t)的转速曲线,利用此转速信息求取等角度重采样的鉴相时标Tn(n=1,2,…,N),并对等时间间隔采样的仿真信号x(t)进行三次样条插值计算,所得的等角度间隔重采样信号,如图7 所示。对重采样信号进行快速傅里叶变换,求取其阶次谱,如图8 所示。

图5 IMF1 分量Hilbert-Huang 时频图Fig.5 The Time-Frequency Spectrum of IMF1
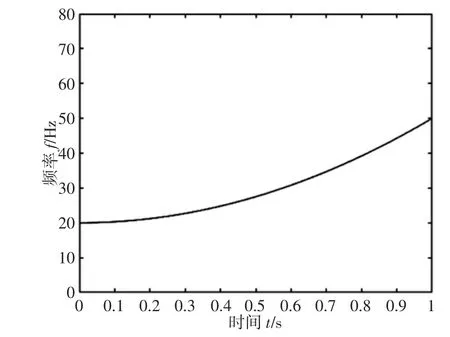
图6 x(t)时频曲线拟合Fig.6 Fitted Time-Frequency Curve of x(t)
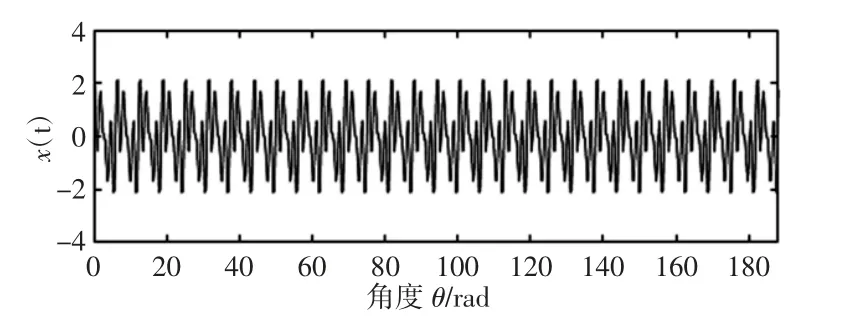
图7 x(t)角域重采样Fig.7 Angular Resampling Waveform of x(t)
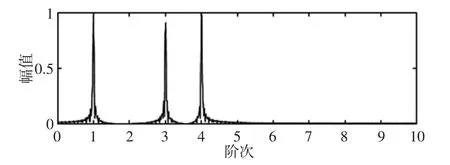
图8 x(t)的阶次谱Fig.8 Order Spectrum of x(t)
从图8 中可以看出该信号包含了阶次分别为1、3、4 的三个信号分量,与原始仿真信号x(t)各分量之间的频率相符。通过对该多分量非线性调频信号的仿真充分验证了无转速计阶次分析方法的有效性,因此该方法能够进行启动电流信号的分析。
4 齿轮箱故障诊断实验
4.1 试验平台
齿轮箱试验平台可分为电机控制模块和转子系统模块,如图9 所示。

图9 齿轮箱试验平台Fig.9 The Test Platform of Gear Box
主要组成部分有调速电机、齿轮箱、双跨转子系统、磁粉制动器和传感器等。变频调速三相异步电机通过齿轮箱拖动双跨转子轴系转动,磁粉制动器与轴系相连提供负载。其中,三相异步电机采用变频调速,额定电压380V,额定电流5.1A,额定功率2.2kW,额定转矩14.9N·m,额定转速1500r/min;磁粉制动器的输出范围(0~4)A;齿轮箱为一级传动,本实验配备的齿轮组的模数为2,主动轮齿数55,从动轮齿数75,材质为S45C,齿轮组包含无故障和断齿故障两个从动齿轮,如图10 所示。根据需要更换从动齿轮即可实现故障源的设置。

图10 断齿从动齿轮及完好从动齿轮示意图Fig.10 Schematic Diagram of Broken Driven Gear and Intact Driven Gear
4.2 测试系统
试验测试系统主要由WBI021F27 交直流电流传感器和DH5923N 动态测试信号采集分析系统构成。其中,交直流电流传感器采用电磁感应和霍尔效应原理,可以对启动电流信号进行实时测量;动态测试信号采集分析系统为通用型信号分析系统,可实现对采样数据的实时监测以及采样数据的传输与初步分析。
4.3 实验方案
(1)实验系统通过更换从动轮的方法施加断齿故障激励,并针对同一种齿轮状态下的电机转速(电流基频)、磁粉制动器输出值等参量设计三因素三水平正交实验,其因素水平表,如表2 所示。

表2 因素水平表Tab.2 Factors and Levels Table
(2)在已经建立好的齿轮箱试验平台上,对不同情况下的电机启动电流信号进行采集。本实验中,采样频率为5000Hz,单次采样时间为10s,每次采样间隔为10min。
4.4 实验结果
采集到的启动电流信号时域波形,如图11 所示。其时域图并无明显故障特征。对其进行快速傅里叶变换求取幅频特性曲线,如图12 所示。由于其频谱图存在明显的“频率模糊”现象,仍然无法对信号进行有效地分析。对启动电流信号进行等角度重采样,其角域重采样波形,如图13 所示。由图13 可知,经等角度重采样后,时域的非平稳启动电流信号转换为角度域的平稳信号。
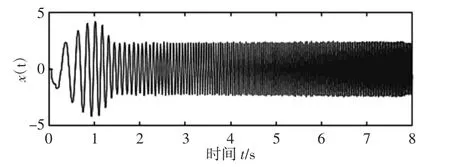
图11 启动电流信号时域波形Fig.11 Time-Domain Waveform of Startup Current
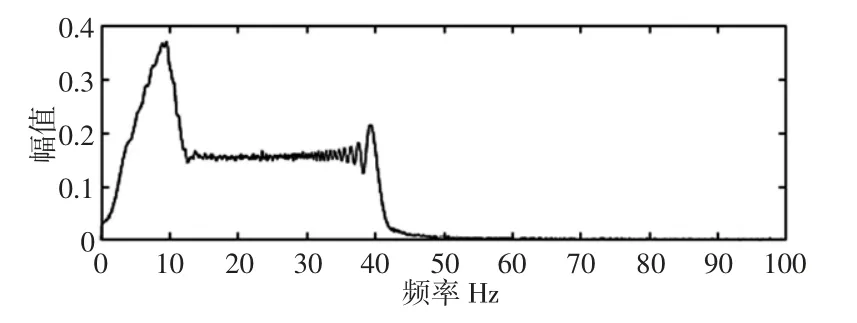
图12 启动电流信号频谱图Fig.12 The Spectrum of Startup Current
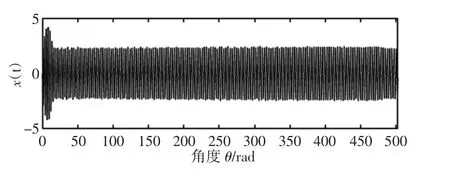
图13 启动电流信号等角度重采样波形图Fig.13 Angular Resampling Waveform of Startup Current
对重采样信号进行阶次分析,其中电流基频为40Hz、磁粉制动器输出值为0.30A 时,齿轮状态分别为无故障与断齿故障的启动电流信号的阶次谱,如图14、图15 所示。
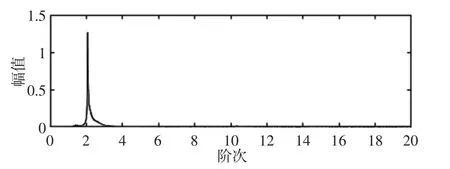
图14 40Hz 无故障启动电流信号阶次谱Fig.14 Order Spectrum of No-Fault-Gear’s Startup Current(40Hz)
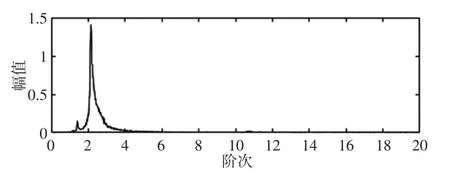
图15 40Hz 断齿故障启动电流信号阶次谱Fig.15 Order Spectrum of Broken-Gear’s Startup Current(40Hz)
以上启动电流信号阶次谱表明,齿轮箱启动电流信号有明显的阶次分量为2 的阶次峰,这是电流信号的特征阶次。当有断齿故障时,会出现阶次分量为1.5 左右的阶次峰,这是由于断齿故障产生的特征阶次,据此可以进行齿轮箱断齿故障诊断。实验研究发现,随着负载(磁粉制动器输出值)的增大,故障特征分量越来越明显。
5 结论
针对采样电机驱动的齿轮传动系统在故障诊断中的特点及存在的问题,提出了一种基于电机启动电流的无转速计阶次分析方法,并给出了具体步骤。通过理论和仿真分析以及实验验证,实现了基于电机启动电流对齿轮断齿故障的诊断。
(1)当齿轮发生断齿故障时,会产生与从动轮转频相关的冲击载荷作用,致使系统产生附加的波动转矩,从而导致在定子电流中产生非线性的电流信号。因此,在无故障电流信号的特征阶次的基础上出现一个新的故障特征阶次,据此可有效识别断齿故障。
(2)通过无转速计阶次分析,时域的非平稳启动电流信号转换为角度域的平稳信号,使得常规频谱处理方法在启动电流信号故障诊断中的应用成为可能,为解决因转速波动带来的“频率模糊”现象以及实际工作无法加装转速传感器等问题提供了有效的解决方法。

