海底边坡参数化建模及稳定性评价研究

祁 磊 ，姚志广 ，许 浩 ，邓海峰 ，李 春

中国石油集团工程技术研究有限公司，天津 300451

中国石油天然气集团海洋工程重点实验室，天津 300451

随着海洋油气开发力度的加大，海洋工程地质灾害的影响逐渐受到重视。海洋工程地质灾害包括海底滑坡、浅层气、天然气水合物、断层、浅层流及潮流沙脊等。其中因边坡稳定性不足导致的海底滑坡对海洋工程开发的影响最大[1]。

目前对海底边坡的评价包括边坡稳定性分析及边坡失稳对结构的影响两个方面。边坡失稳对结构的影响分析方法包括有限元法、欧拉拉格朗日耦合法（CEL）及目前较为流行的光滑粒子法（SPH）等[2]。边坡的稳定性分析评价方法还是主要借鉴陆上边坡稳定性评价方法[3]，包括：工程类比法、极限平衡法、数值分析法、模型模拟试验方法等。

这些方法中，以瑞典条分法、Bishop法等为代表的极限平衡法在陆上边坡评价中应用较广，但其用于单一均质土层较合适，用于层状土存在困难。极限平衡法中的强度折减方法在岩土工程的边坡稳定性分析中逐渐得到应用。

1 基于强度折减的海底边坡稳定性计算分析方法

强度折减法中的稳定安全系数与极限平衡分析中所定义的土坡稳定安全系数在本质上是一致的。具体是：将土体的抗剪强度指标黏聚力C和摩擦角φ用一个折减系数Fs进行折减[4]：

式中：CF为折减后土体黏聚力，φF为折减后土体内摩擦角，τfF为折减后的土的抗剪强度，σ为法向应力。

强度折减法能够对复杂地貌、地质的边坡进行计算；同时考虑了土体的本构关系及变形对应力的影响；能够通过剪应变增量或位移增量给出边坡的滑移面形状，且不需要假定滑移面的形状；也适用于层状土层。ABAQUS有限元软件具有通过定义场变量实现强度折减法计算边坡稳定性的能力。失稳标准主要有位移vs场变量法（如图1所示）、塑性区贯穿法（如图2所示）、不收敛法等[5]。

图1 位移vs场变量法

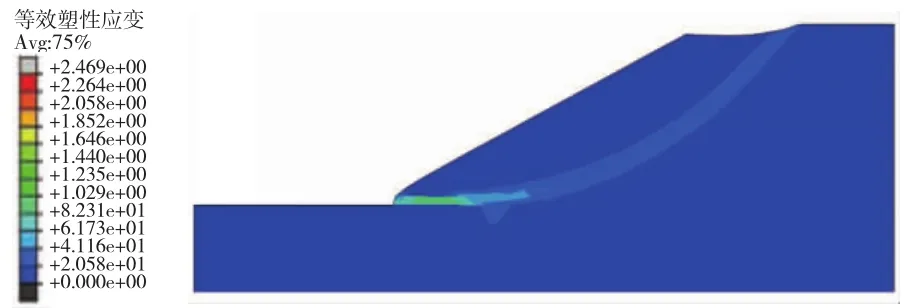
图2 塑性区贯穿法

2 海底边坡波压力的计算

对于水深较浅的滩浅海，波浪会对其下方的海床产生波压力作用；对于海底边坡，这种压力会施加至坡体的表面。随着波浪的传播，变化的荷载会改变坡体内土体的应力，如果这个应力值超过了土体强度，就会发生边坡失稳。

本文对波浪力作用下的海底边坡稳定性进行计算基于线性波浪理论，在一阶线性波浪理论中，假设波浪以正弦波的形式传播（如图3所示）。

图3 波浪引起的海床波压力

海床波压力的计算公式为：

式中：P为海床波压力，x为波浪传播距离，L为波长，t为时间，T为波周期，P0为波浪引起海底压力变化的幅值，γw为海水重度，H为波高，d为水深。

由于实际工程中所提供环境参数（如设计文件）通常仅包括波高、水深和周期值，而波压力需要相对应的波长值，本文采用牛顿迭代法按照下式进行计算：

式中：L为波长，d为水深，T为波周期。

采用Python语言开发了牛顿迭代法计算程序，可计算出不同水深、周期下的波长数据，部分程序代码如图4所示。

图4 基于牛顿迭代法的波长计算代码

计算参数选取珠江口海域典型波浪、水深等水文参数。该海域海底地形较为复杂，由于该海域为我国重要的经济水道，航道、海管、锚地分布复杂，还存在众多采砂坑。水深范围2.85～33.5m。根据相关资料，该海域有效波高周期数据见表1。

表1 有效波高、周期数据

采用牛顿迭代法对该海域不同水深下的海床波压力进行了计算，计算结果如图5所示。

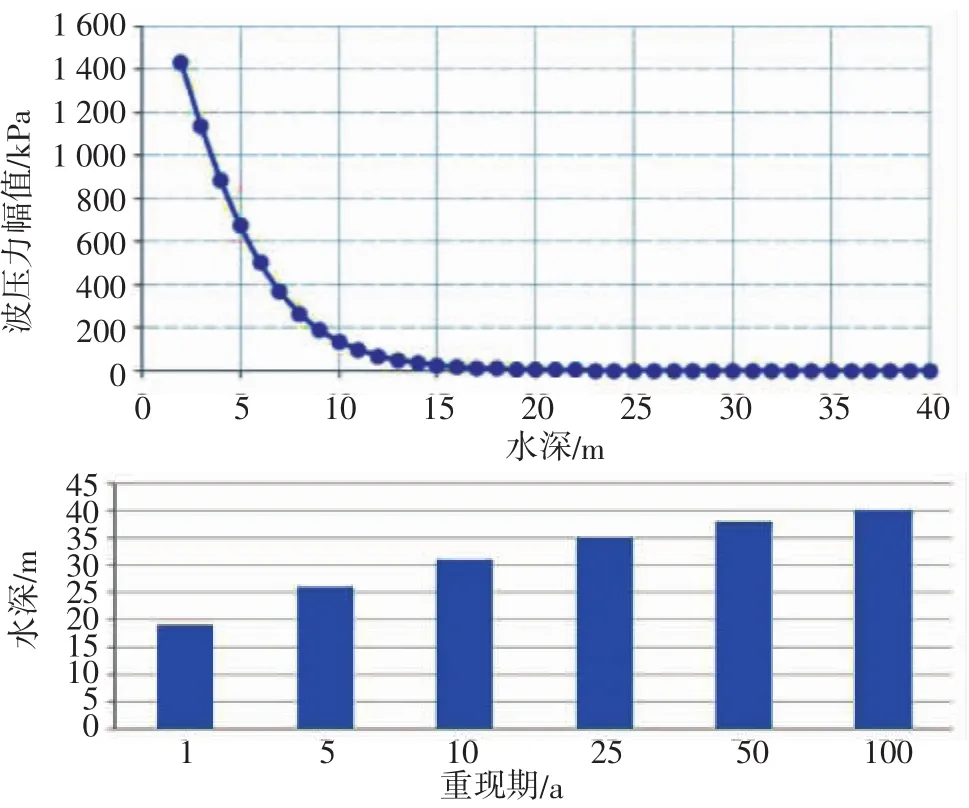
图5 波压力与水深关系

由图5可以发现：水深越深，波压力幅值越小；随着波浪波高和周期的增大，波压力逐渐变大。在坡底水深较深情况下波压力很小，在滑坡稳定性中，波压力主要作用在坡顶和坡体位置，致使滑移力增加；同时由于波浪载荷是周期性载荷，会导致海床的粒状土超孔压增加、抗滑力降低。因此海床波压力会促进边坡发生失稳，尤其当水深较浅时计算中不可忽略波压力的影响。

3 边坡稳定性分析参数化建模

对于部分海底边坡，由于采砂等人为因素或复杂的海洋水文及工程地质条件影响，致使整个边坡各处的坡角、坡高差异巨大。如图6所示的珠江口某实际工程中，边坡坡角为2°～20°，采用单一坡高、坡角值将不具代表性，而采用三维边坡稳定性分析方法将大大增加计算工作量。由于采用强度折减法进行边坡稳定性分析时，三维和二维的计算结果差别不大[6]，因此，本文在计算此类型边坡中，仍旧采用基于平面应变的二维模型，同时在选择坡体时通过人为从多波束数据截取或基于地理信息系统的最大坡降法等来选择需要计算的坡体。

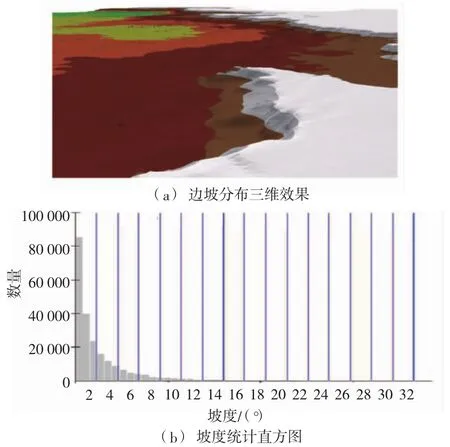
图6 珠江口海域某海底边坡分布情况

3.1 边坡坡体参数化建模

边坡坡体建模模块自动读取多波束等数据，建立边坡模型。代码通过读取边坡的坐标数据，将其换为ABAQUS模型数据。由于水深地形数据只在边坡位置剧烈变化，为方便后期划分网格及计算分析，距离边坡位置一定距离的坐标设为定值，忽略其微小变化，部分关键代码如图7所示。

图7 边坡坡体建模模块部分程序代码

3.2 土层自动分层附属性

采用ABAQUS计算边坡的稳定性采用的是强度折减法，需要对每一层土的黏聚力、摩擦角以场的形式进行折减，对于层状土质边坡，每一层的土体参数都不同，本文采用Python语言编写了如图8所示的自动分层附属性模块，进行边坡属性的赋值，所建立的有限元模型如图9所示。

图8 土层自动分层附属性部分代码

图9 参数化建模建立的模型（自动分层附属性）

3.3 载荷（重力、波压力）自动施加

对于层状土质边坡，每一层的浮容重、土体参数都不同，可根据由上到下的土层分层特点进行参数化附属性。荷载自动施加部分源代码如图10所示，施加后的数值模型如图11所示。

4 工程应用及分析

图10 载荷自动施加程序代码

图11 参数化建模（自动施加载荷）

基于ABAQUS的边坡稳定性参数化建模分析在多次的海洋工程地质灾害评价中得到应用，大大提高了计算效率。以珠江口某工程为例，该场址土体参数如表2所示，为非常典型的层状土质，表层土强度较弱，砂层中间加软弱薄黏土层；该位置坡顶水深在2 m左右，坡高超过30 m，坡角变化范围为 2°～20°。

表2 某钻孔位置土体参数

计算中将海床波压力按照静载施加，由于一个周期内同一位置不同时刻所受波压力不同，将一个周期分成8段，计算一个周期内不同时刻边坡稳定性的变化，如图12所示。

图12 一个周期内不同时刻边坡稳定性安全系数变化情况

可以发现，不同时刻边坡安全系数存在差异，但都较不考虑波浪载荷时小，可见波浪对边坡稳定性会产生影响。同时由于计算中将波浪按照静载进行施加忽略了动态载荷放大作用，且没有考虑波浪造成的超孔压会使土体抗剪强度降低，这两种因素都将促进边坡发生失稳，因此在滩浅海地区，尤其是易受台风等极端天气影响的海域边坡稳定性分析需要考虑波浪载荷的影响。

计算云图如图13所示，从图中可看出计算分析出的坡体与单一均值土层不同，不是连续的圆弧，而会在土层抗剪强度变化显著的地层（如黏土层和砂土层交界处）发生明显的变化。

图13 边坡稳定性分析结果

5 结束语

本文主要探讨了实际工程中建立边坡有限元模型的参数化建模方法，并采用强度折减法进行不同坡角下边坡稳定性评价，计算中考虑了因波浪作用对海床土应力的影响，发现波浪对边坡稳定性会产生一定的影响，由于动态载荷放大作用及波浪产生的超孔压会使土体抗剪强度降低，都将促进边坡发生失稳，因此在滩浅海地区，尤其是易受台风等极端天气影响的海域边坡，其稳定性分析需要考虑波浪载荷的影响。参数化建模大大提高了实际工程计算分析的效率，可为实际工程中的海洋边坡稳定性评价提供参考。