如何理解“推理”

□杨润歌 郜舒竹

《义务教育数学课程标准（2011年版）》（以下简称《课标》）中指出，在数学课程中，应当注重发展学生的推理能力。推理是人们日常生活和学习中经常使用的思维方式，它一般包括合情推理和演绎推理。在解决问题的过程中，两种推理的功能不同，相辅相成：合情推理用于探索思路，发现结论；演绎推理用于证明结论。《课标》中主要强调了演绎推理、归纳推理和类比推理，需要进一步思考的问题有：这几种推理形式之间的关系是什么？是否还有其他的推理形式？推理能力指怎样的数学能力？

一、推理

人的思维方式包括概念、判断和推理，其中推理（Reasoning）是指从一个命题判断到另一个命题判断的思维过程。[1]对于这种思维形式可以从形式逻辑推理和辩证逻辑推理进行深入认识。

（一）形式逻辑推理

形式逻辑包括演绎逻辑和归纳逻辑的内容，它指撇开具体的、个别的思维内容，从形式结构方面来研究命题。演绎逻辑是以演绎推理为基本内容的逻辑体系，其中演绎推理指由一般性知识为前提推出个别性知识结论的推理。而归纳逻辑是以归纳推理为基本内容的逻辑体系，其中归纳推理是从个别性知识为前提推出一般性知识结论的推理。

演绎推理与归纳推理均是由前提推出结论的过程，只不过演绎推理是由一般到特殊的过程，前者涵盖的知识内容要大于后者，按这一思维方式进行推理得出的结论必定是正确的，因此演绎推理亦可称为必然推理。相反，归纳推理是由特殊到一般的过程，其中的完全归纳推理为必然推理，不完全归纳推理则为合情推理。

类比推理是根据两个或两类对象某些属性的相同，推出它们的其他属性也可能相同的推理。类比推理是一种合情推理，其可靠程度取决于“前提中确认的共同属性的多少以及共同属性和类推出来的属性的关系是否密切”。[2]因此，按必然推理与合情推理的分类标准对《课标》中的相关内容进行整理，如图1所示。

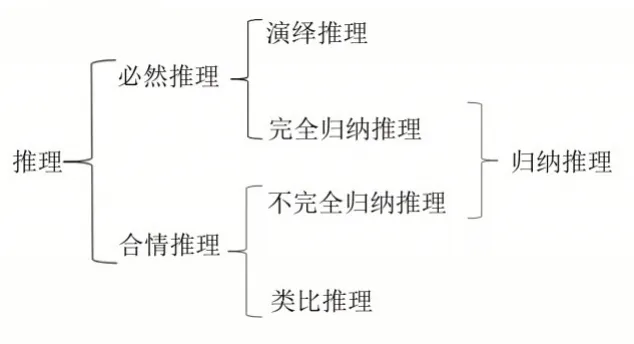
图1 部分推理形式关系图

《课标》中谈及“教师在教学过程中，应该设计适当的学习活动，引导学生通过观察、尝试、估算、归纳、类比、画图等活动发现一些规律，猜测某些结论，发展合情推理能力”。但图1的推理关系表明，归纳推理并非全部属于合情推理的范围，而仅指归纳推理中的不完全归纳推理。

在形式逻辑的学科视野中，推理前提的真实性是由各门具体科学给定的，是各门具体科学研究的对象，形式逻辑本身是无从证实其前提内容真实性的。[3]也就是说形式逻辑推理是从具体推理中抽象出推理形式进行研究，只要满足其同一律、矛盾律和排中律即可，无须考虑内容。这就使得《课标》中关于“通过实例使学生逐步意识到，结论的正确性需要演绎推理的确认”的说法，更值得细细推敲，即进行演绎推理的前提不一定都是正确的。

（二）辩证逻辑推理

辩证逻辑不是关于思维的外在形式的学说，它研究概念的矛盾和转化，是现实的矛盾运动在思维运动中的反映。[4]概念间的组合会形成命题或判断，而推理又是从一个判断到另一个判断的过程，因此概念、判断和推理三者之间环环相扣。辩证逻辑将概念中的矛盾继续延伸到推理中。矛盾的普遍性决定了当以辩证的眼光看待问题时，任何事物都是对立统一的存在，也就是矛盾具有客观性，这种矛盾是无法消除或避免的。

在形式逻辑中也存在矛盾律，是指某一命题或判断不能既为真又为假。只要遵守这条规律，注重命题或判断的描述，矛盾是可以避免的，这一点与辩证逻辑有所不同。《课标》关于“证明命题时，应要求证明过程及其表述符合逻辑，清晰而有条理”这一表述中的“符合逻辑”是符合形式逻辑。一是指推理形式符合规律，主要是指矛盾律。若按形式逻辑理解矛盾律自然可以避免，但若以辩证思维来考虑问题，矛盾一定存在就不合乎逻辑了。二是忽略了推理内容。比如人教版小学数学四年级下册出现的“鸡兔同笼”问题，其中一种解题想法是“使鸡抬起一只脚”以及“兔抬起两只脚”，进而推理出鸡兔各为多少。[5]这一过程中出现的“是鸡”“非鸡”与“是兔”“非兔”的内容情境是存在矛盾的，显然也不符合形式逻辑。

形式逻辑推理与辩证逻辑推理各有其特性，二者相辅相成，可以从形式与内容两个角度以辩证思维看待推理形式。《课标》中将合情推理与演绎推理作为两种相辅相成的推理形式，强调“‘证明’的教学应关注学生对证明必要性的感受，对证明基本方法的掌握和证明过程的体验”。此处似乎将推理能力的发展寄托于证明题，并在附录中出示了相关例题（参见《课标》例62）。事实上，推理不仅存在于证明题中，在应用题的求解、知识点的学习等内容中均有体现，且推理形式不拘泥于《课标》中所谈及的。

二、多样性

推理的教学往往不会孤立存在于某一板块内容与某几种形式之间，因此除《课标》中谈及的演绎推理、归纳推理和类比推理外，推理的形式是多种多样的。

（一）比例推理

比例推理（Proportional Reasoning）是关于数量关系的思考，要求同时对几个数量或值做出比较。[6]在小学数学教科书中比例推理常以缺失值的形式呈现。如“小明骑行4千米用时20分钟，小刚同速骑行12千米需要多长时间？”对于该问题，可以从以下三个角度思考。其一“一份是多少”的策略，根据小明的骑行信息可知二人的骑行速度为1分钟行驶千米，或行驶1千米用时5分钟，此时再运用速度、时间与路程的数量关系即可求得小刚的用时。其二“倍数有多少”的策略，小刚比小明多走了3倍，所用时间亦为3倍关系。其三“交叉相乘”策略，利用二者同速的条件列方程求解。[7]前两种策略是建立在学生生活经验之上的一种直观方法，而第三种策略是学生惯用的一种算法，只要遇到相似形式的方程就会做出的一种操作，因此，需要进一步思考这种算法背后的算理是什么。

除了缺失值形式的比例外，也存在不依赖于任何特定数值而进行的比例推理。比如“两片鱼塘，A鱼塘的面积大于B鱼塘面积，但是A鱼塘中的鱼苗数量少于B鱼塘中的鱼苗数量，问哪片鱼塘的鱼苗密度更大？”此时不需要具体数值即可推理得出B鱼塘中的鱼苗密度更大。

比例推理的应用也较为广泛，例如地图上的比例尺、比较哪种商品更划算以及溶液浓度等等。因此，要用联系的眼光来看待推理，它既存在于数学中，也存在于日常活动中。

（二）协变推理

协变推理（Covariational Reasoning）是协调两个变量，同时关注它们彼此之间变化方式的认知活动。[8]在中学数学课程中的函数，协变推理表现得更为突出，以一次函数和指数函数为例进行说明。一次函数的一般式如y=kx+b（k、b是常数，其中k≠0），当自变量x变化时，因变量y也会随之变化。而k表示该函数的斜率即方向，因其为常数所以不随x的变化而变化，常数b的变化只改变函数图象上下移动的位置。指数函数的一般式如y=ax（a为常数，且a>0，a≠1），其图象如图2所示。因变量y会随自变量x的变化而变化。在a从0趋近于无穷大（以为例）的过程中（不包括a≠1），函数的曲线从分别接近于y轴与x轴正半轴的单调递减函数的位置，趋向分别接近于y轴与x轴负半轴的单调递增函数的位置。

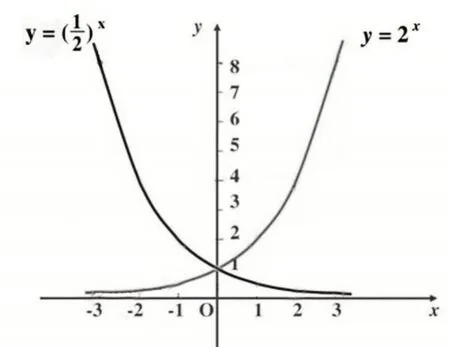
图2 指数函数图象

从这两种函数中可以看出，当常数值不变时，一个变量的变化会引起另一个变量的变化；当两个变量不变而常数值发生变化时，函数图象的位置会改变。也就是说，当任一量变化时，总会有另一个量协同变化。

再如整个宇宙中的能量均遵循能量守恒定律，进行自由落体的铁球在坠落过程中存在重力势能与动能的转换，也可看作是两个量的协变过程。可见，协变推理强调的是部分与部分、部分与整体间的联系。所谓部分间的联系是指两个变量间的变化方式，如因变量随自变量变化，抑或是能量之间相互转换。部分与整体的联系是指通过部分间的联系而使整体一直处于一种稳定平衡的状态，如无论因变量和自变量怎样变化，始终满足某一函数的表达式，抑或是总能量的守恒。因此，在进行推理的过程中，可将部分与整体联系起来进行思考。

（三）变换推理

变换推理（Transformational Reasoning）是通过改变原有问题情境形成新的状态或状态连续体。[9]变换推理是指从情境入手对某一问题的思考打破常规。比如“从家到超市，爸爸要走12分钟，小明要走15分钟，爸爸的速度比小明快百分之几？”有的学生可能认为“比谁除谁”即（15-12）÷15=0.2=20%，未意识到题目中给出的是时间关系，而非速度关系，所以此种做法是错误的。可以通过线段图的方式进行求解，将题目中的时间关系转化为路程关系，如图3所示。其中A部分与B部分分别表示爸爸和小明在12分钟内走的距离，C部分表示在12分钟内爸爸比小明多走的距离。根据速度乘时间等于路程的关系式，速度与路程成正比，因此题目中问二人的速度关系可转化为路程关系，此时根据线段图可以得出（15-12）÷12=0.25=25%，即爸爸的速度比小明快25%。

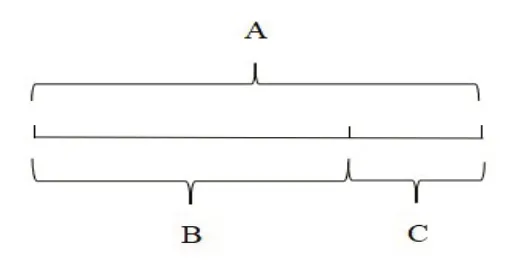
图3 路程线段图

此问题也可采用变换推理改变问题情境，假设父子二人均步行60分钟，此时爸爸按之前的速度可以走5趟，小明走4趟，（5-4）÷4=0.25=25%。其解题的本质与线段图解法一致，均借助父子二人的路程关系求解。通过比较可以发现，线段图解法采用数形结合的思想，能够明晰题目中的数量关系，而变换推理从情境入手简化问题降低计算难度，二者对同一问题的解决殊途同归。

推理存在于数学与生活之中，而在数学中不仅仅局限于《课标》中谈及的证明题，它贯穿于数学课程的各个内容中，这体现了推理的普遍性。推理作为一种思维方式的存在，其形式是多种多样的，不可能被穷尽，要时刻以联系与变化、部分与整体的观点进行思考，这体现了推理的联系性。对于推理的正确认识将有助于思考如何将其作为一种数学能力渗透到数学课程与教学中。

三、推理的能力

推理能力是借助推理的数学思维方式以解决问题的能力。推理的过程一定要让学生亲身经历，让学生不但要知其然，还要知其所以然。也就是说，学生知道某种形式的算法往往是不够的，还要明白其背后的算理。

正如前文中提到的“交叉相乘”算法，其计算法则背后隐藏着推理。教师可将题目中小刚需要的时间设为x分钟，其分数方程表达式为而后可改写为20÷4=x÷12。再根据等式的性质，等号两边同时乘或除以同一个不为0的数，等式仍然成立，因此变形为20÷4×12=x，此时再将其改写回分数形式这样就能明白计算口诀的意义了。

再如中学数学课程中的指数运算“3-2×3-3=3-5”，学生记住了“底数相同，指数相加”的计算规则，而规则中同样隐藏了推理。即2个与3个相乘，得到的5个就是=3-5。

这是一种“如何（How）”与“为什么（Why）”之间的差距，中间缺失的桥梁正是推理，而导致桥梁缺失的原因是学生为了追求“又对又快”的结果，逐渐忽视算理。另外，在学习某一知识时，除了追根溯源探求其所以然外，还应注意一种内容的学习可以有多种推理形式。

在比的学习内容中可以涉及类比推理、比例推理和协变推理。首先是类比推理，比的内容并非初次接触，是由除法到分数再到比。除法中的被除数是分数中的分子，是比中的前项；除法中的除数是分数中的分母，是比中的后项；除法中的商是比中的比值。因此运用类比推理，得出比也具有与除法和分数相同的性质，即比的前项和后项同时乘或除以相同的数（0除外），比值不变。其次是比例推理，利用比可以配置不同浓度的溶液，以及同一浓度不同容积的溶液。最后是协变推理，要想得到同一浓度不同容积的溶液，浓缩液与水的体积也就是比的前项和后项要协同变化，来保证浓度即比值不变。由此可看出比例推理与协变推理有共通之处，且在配制溶液问题中，二者均利用了比的性质。这也说明推理不仅与数学和日常生活有联系，而且不同推理形式之间也是有联系的。

因此，数学教学中培养的推理能力，应当是用联系与发展的眼光看待问题的综合能力。

综上，推理作为一种思维形式，要将推理的形式结构与内容结合起来辩证地加以认识。在知识学习以及问题解决过程中存在多样的推理形式，它们之间相互联系，并不是彼此割裂的对立面。