关注“生长力”的概念教学
——以“倍的认识”教学为例
□沈建芳
在小学数学概念中,“倍”是一个抽象而重要的概念。理解和掌握“倍”的概念,有利于学生解决生活中的一些实际问题,也可以为后续学习分数、比例等知识奠定基础。在学习本课之前,学生有怎样的知识经验基础?如何突破概念的灌输式教学?怎样让学生亲历概念的形成过程?学生的“生长力”在哪?带着这些思考,笔者展开了研究。
一、课前调研
为了了解学生是否知道“倍”是表示两个量之间的关系,笔者进行了前测。前测单如图1所示。
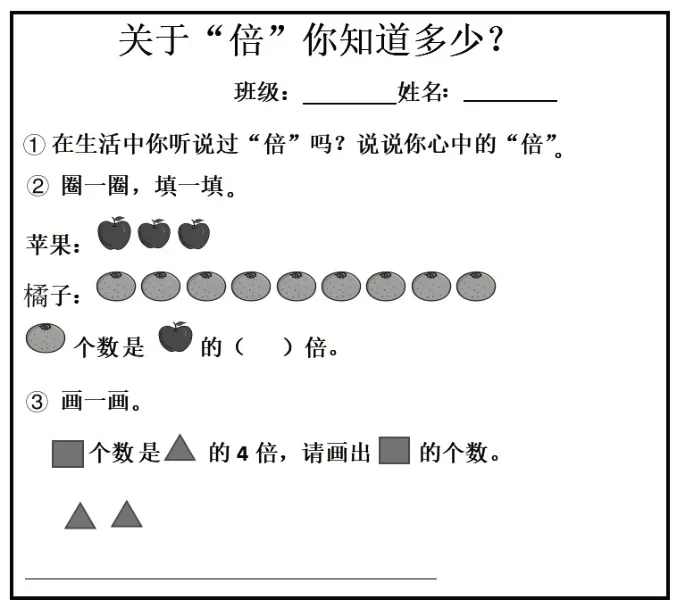
图1
调查发现,第①题,有95.6%的学生认为自己在生活中是认识“倍”的,但在表述心中的“倍”时,有22.2%的学生能用“谁是谁的几倍”的句式;有11.1%的学生能用“谁是多少,谁是多少,谁就是谁的几倍”的句式;其余学生的表述不是很清晰,有些甚至是错误的。第②题,受相差关系的影响,有26.7%的学生认为橘子比苹果多6倍。第③题,有26.7%的学生把长方形是三角形的4倍理解成长方形比三角形多4个,所以画了6个长方形,有17.8%的学生画了4个长方形。
二、解读教材
前测结果表明,学生对“倍”的概念或没有太多的认知和感受,或模糊不清。学生学习“倍”要经历认知结构上的转变,从原先两个量之间的“差比”结构转变为“倍比”结构。如何改变学生原有的认知,优化“倍”的教学,笔者从解读教材入手,选取了北师大版、人教版、苏教版、浙教版教材,进行分析比较。
(一)四个版本教材编排情况
北师大版教材以“快乐的动物”为情境,抓住动物数量之间的比较,通过画一画、圈一圈、认一认、填一填等活动,把3只小猴圈在一起看作1份,小鸭有6只,可以圈2份,用除法表示6÷3=2,6里面有2个3,就说小鸭的只数是小猴的2倍。
苏教版教材以“小朋友数花”为情境,通过问题“你能比一比这三种花的朵数吗”展开教学。教材先呈现学生以前学过的“比多比少”的方法,接着通过圈一圈,用“倍比”的方法进行比较,得出黄花是蓝花的3倍。
人教版教材以“小兔子数萝卜”为情境,先数一数,接着圈一圈,把2根胡萝卜看作1份,红萝卜可以圈这样的3份,红萝卜的根数里包含3个2,就说红萝卜是胡萝卜的3倍;白萝卜可以圈这样的5份,白萝卜的根数里包含5个2,就说白萝卜是胡萝卜的5倍。
浙教版教材以“游艺室里挂气球”为情境,把2个红气球看作1份,蓝气球有这样的3份,就说蓝气球的个数是红气球的3倍。接着通过挂气球的个数变化来呈现“标准量”“比较量”“倍数”之间变与不变的关系。
(二)四个版本教材编排异同
比较这四个版本教材编排的异同,笔者发现,四个版本的教材都没有直接给“倍”下定义,都是创设具体的情境,通过数一数、圈一圈等操作活动将新知嫁接在原先“几个几”和“份数”的理解基础上,帮助学生建构“倍”的含义。不同之处在于北师大版教材将“倍”与除法相联系,除法不仅可以表示平均分问题,还可以表示两个数量之间的“倍”数关系;苏教版教材呈现了两种比较的方法,让学生对两个数量的比较的认知从原先的“差比”过渡到“倍比”。人教版和浙教版都没有呈现差比关系,都是在“几个几”和“份数”的认知基础上让学生理解“倍”的含义,对“倍”表示两个量的比较关系体现不够。浙教版通过挂气球的个数变化,呈现了“标准量”“比较量”“倍数”之间的变化关系。

三、重构课堂
笔者根据各版本教材的特点,重新设计了教学方案。
(一)经验入手,引入“倍”的学习
教学中要关注学生已有的生活经验和知识经验。学习本节课之前,学生对“倍”不是一无所知,教师在课前可以通过谈话的形式了解学生已知的“倍”。另外,学生对“倍”的学习也要建立在原有的知识经验基础上,在与“差比”关系的认知冲突中,引出“倍比”关系。
【教学片段1】
师:大家听说过“倍”吗?说说你心中认识的倍。
生:我妈妈叫我加倍学习,期末给我奖励。
生:我在电视上看到“产值翻倍增长”,倍就是很多的意思。
生:爸爸的年龄是我的4倍。
师:你能解释一下这句话的意思吗?
生:爸爸的年龄比我大4倍。
……
师:刚才同学们都列举了生活中自己所理解的“倍”,那数学中的“倍”又是怎样的呢?
【教学片段2】
师:湖边来了一群可爱的小动物(屏幕呈现),有多少小动物呢?请你数一数。(生说师板书)
师:谁来比一比小松鼠和小鸡的只数?
生:小鸡比小松鼠多6只。
生:小松鼠比小鸡少6只。
师:是的,我们在二年级时学过比多比少,知道可以用比多比少的方法对两个量进行比较。还可以用其他的方法进行比较吗?(学生沉默)
师(提示):我们还可以用倍的方法进行比较。今天这节课,咱们就一起来研究有关“倍”的知识。(板书课题:“倍”的认识)
(二)操作感悟,建构“倍”的模型
本节课是学生第一次学习“倍”,也是认知上的一次改变。所以,教学要借助“比一比,说一说”“圈一圈,填一填”“想一想,摆一摆”等操作活动,让抽象的“倍”在具体的活动中变得形象可感,使学生通过活动建构“倍”的模型。
1.比一比,说一说
语言是思维的外壳,通过具体的例子让学生用语言表述“倍”的概念,对“倍”有一个初步的感知。
【教学片段3】

师:如果把3只松鼠看作1一份,小鸡可以分成这样的几份?
生:小鸡可以平均分成3份。
师:小鸡只数有小松鼠这样的几份?
生:小鸡只数有小松鼠这样的3份。
师:所以我们说,小鸡只数是小松鼠的3倍。
师:谁能像老师刚才说的一样再来说一说?
……
2.圈一圈,填一填
通过“圈一圈,填一填”活动,学生明确了“以谁为标准”,建立1倍数的概念,形象地感知“几份数”,理解“一个数包含几个几,这个数就是另一个数的几倍”。学生通过具体活动,理解了“倍”的本质内涵。
【教学片段4】
问:小猴的只数是孔雀的几倍?(练后反馈)

师:把谁看作1份?
生:把2只孔雀看作1份。
师:小猴的只数是孔雀的几倍?
生:小猴的只数是孔雀的3倍。
师:你是怎么想的?
生:小猴有6只,2个是1倍,6里面有3个2,所以小猴是孔雀的3倍。
师板书:6里面有3个2,所以6是2的3倍。
……
3.想一想,摆一摆
教师通过创设四次摆卡片活动,使学生明白确定标准量1份数的重要性。在摆一摆中,学生感知到1倍数、几倍数、倍数三者之间变与不变的关系,对“倍”有了一个完整的认知。
【教学片段5】
师:调皮的小动物们欢快地嬉戏着,小鸭子和小猴子陆陆续续地来了一只又一只,老师将他们的只数用表格做了记录。请你用学具摆一摆,每一次猴子的只数是鸭子的几倍?
反馈交流:
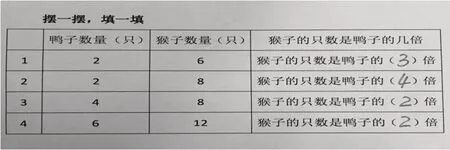
师:观察上下两行鸭子和猴子的数量以及它们之间的倍数关系,想一想什么变了,什么没变。请你任意选择两行比一比。可以跟同桌交流一下。
(1)师:谁先来说说想法?
生:第1次和第2次,鸭子只数没变,猴子只数变了,倍数变了。
师追问:鸭子只数没变,为什么倍数会变了呢?
生:因为第1次的6里面包含3个2,第2次的8里面包含4个2,所以它们的倍数不一样。
生:虽然鸭子的数量没变,但是猴子的只数变了,所以倍数就变了。
……
师小结:是的,1倍数不变,但是与1倍数比较的这个数量变了,所以倍数也就变了。
(2)师:谁还有不同的发现?
生:第2次和第3次,鸭子只数变了,猴子只数没变,倍数变了。
师追问:刚才与1倍数比较的猴子数量变了,所以倍数变了,现在猴子数量没变,为什么倍数也变了呢?
生:因为把鸭子看作1份,这个1倍数变了。
师:是的,我们还发现1倍数增加了,倍数反而减少了。谁能解释一下这个奇怪的现象?
生:因为第2次把2只鸭子看作1份,8只猴子里面包含4个2,而第3次把4只鸭子看作1份,8只猴子里面只包含2个4,所以倍数变少了。
……
师小结:是的,同学们说得都非常好。虽然与鸭子比较的猴子的数量没变,但1倍数鸭子的数量变了,所以倍数就变了。
(3)师:再仔细看看第3次和第4次,鸭子和猴子的数量都变了,倍数为什么不变呢?
生:因为8是4的2倍,12也是6的2倍。
生:猴子和鸭子的数量变了,但是猴子包含鸭子的份数没变,所以还是2倍。
生:这个倍数跟猴子和鸭子数量的多少没有关系,要看猴子只数里面包含几个鸭子的只数。
……
师小结:倍数跟两个数量的多少没有直接关系,而是要看一个量里面包含几个另一个量,谁就是谁的几倍。
(三)巩固提升,深入“倍”的内涵
概念教学中,教师要帮助学生区分概念的内涵与外延,以及与之相关联的概念的联系与区别,只有这样学生才能在头脑中清晰概念。“差比”和“倍比”,是两个不同的知识结构,通过比较练习,学生明白“差比”结果是一个具体的量,而“倍比”结果表示的是两个量之间的一种关系。
【教学片段6】

师:通过比一比,我们发现两题相差的个数一样吗?
生:不一样,第①题相差3个,第②题相差4个。
师:两题相差的个数不一样,倍数为什么都是2呢?
生:因为把圆形看作1份,三角形都是圆形的2份。
师:这个倍数跟相差的个数有关系吗?
生:倍数跟相差的个数没有关系。
师:这个2表示什么意思?跟3和4表示的意义又有什么区别呢?
生:2表示三角形有圆形的2份,表示的是份数。
生:2表示的是2份,3和4表示的是相差的个数。
师:是的,这个2只是表示三角形和圆形的关系,是2倍的关系,它不表示确切的个数;而3和4表示的是相差数,是确切的数。
(四)质疑问难,解析“倍”的疑惑
思源于疑,疑问是开启思维的源泉,教师要培养学生质疑的好习惯。课末,教师创设了让学生质疑的环节,学生通过质疑、分析、思考解决问题,从而加深对“倍”的理解。
【教学片段7】
师:通过今天的学习,你们对“倍”还有什么疑问吗?
生:老师,12是4的3倍,能倒过来说4是12的3倍吗?
生:4小一些,怎么可能是12的3倍呢?
生:我知道,倒过来的话应该说,4比12少3倍。
生:不对,倒过来的话应该说4比12少2倍。
师:同学们刚才说的对不对呢?接下来请你拿出笔和纸圈一圈、画一画,看看有什么发现。把你的发现和同桌进行交流。
……
生:老师,我发现反过来的话把12个三角形看作1倍,4个圆就不够1倍了。
生:我发现,谁是谁的几倍,不能反过来说。
生:我发现小数不能说是大数的几倍。
师:那小数如何表示和大数的关系呢?在后续的分数学习中,咱们会进一步探究这个问题。
四、提炼反思——关注“生长力”
具有“生长力”的概念教学,应以学生的发展为本,立足起点根基,设计合理的教学活动,让学生在自主学习、共同探究、互教互学中建构概念。
(一)经验为“根”——立足概念教学“生长”的“根基”
在概念教学中教师应准确分析学生已有的生活知识经验,为概念教学找准起点。
“倍”是生活中的一个常用概念,学生接触过,但是对概念的理解是模糊的。如何将“生活中的倍”转化为“数学中的倍”是本节课的教学重点。“倍的认识”是在学生认识平均分与除法意义的基础上进行的,“倍”表示两个数量间的比较关系,是从“比绝对数量”到“比相对数量”的转变。因此,教师将教学建立在学生已有的“差比”关系的基础上,引出“倍比”关系,把新知“嫁接”在原有知识经验基础上。
(二)活动为“线”——经历概念教学“生长”的“阶梯”
概念教学要关注概念的实际背景以及概念形成的思维过程。抽象的数学概念的形成可以借助有形的数学活动,通过活动铺就概念与学生思维的通道,帮助学生有效建立概念。学生掌握概念的过程也是一个不断发展的过程,往往经历几个阶段。
1.建立概念的表象
概念的表象是指对概念具有鲜明形象的感知,将头脑中的概念经过外部信息进行转化,是对概念进行知识表征的过程。“倍”表示的是两个量之间的关系,虽然学生在生活中对“倍”有初步的感知,但无法用准确的语言描述什么是“倍”。所以教师创设了动物乐园的情境,通过具体的例子表征“倍”的含义。让学生在具体的情境中,结合实例说一说,用语言表征“倍”的含义,在头脑中建立“倍”的表象。
2.抽象概念的本质
概念是事物本质属性的反映。概念的形成是一个从具体到抽象概括的思维活动,教师可在学生通过感知获得概念表象的基础上,引导学生进行分析、综合、概括,从具体到抽象逐步探寻概念的本质。在“倍”的概念教学中,笔者通过创设“比一比,说一说”“圈一圈,填一填”“想一想,摆一摆”的操作活动,让学生多感官参与活动,在探究知识的活动中积累活动经验,抽象出“倍”的本质。
学生在“想一想,摆一摆”四个层面的操作活动中积累经验,确定比的标准,建立“1份”的概念,明确“倍”与“份数”之间的联系;接着,学生想一想,从“直观体验”过渡到“抽象思维”,挖掘“倍”的本质,理解“一个数包含几个几”就是“一个数是另一个数的几倍”,明确“倍”隐藏着“包含”的关系,达到对“倍”的本质的理解。
3.厘清概念的知识结构
数学概念的抽象性与小学生思维的具象性,要求教师在概念教学中不能孤立地讲解概念,要将概念与实例相结合,借助实例让学生形象地感知概念的本质特征,从而厘清概念的知识结构。
教材用谁是谁的几倍这种结构化的语句来表征“倍”的概念,突出两个数量相互比较,把其中较小的量看作1份作为标准,另一个量里面包含这样的几份就是几倍。只要1份的数确定了,另一个量有几份就是几倍。由此可知,这个1份数标准量在“倍”的认识中起着关键作用。教师在教学时要帮助学生厘清“倍”的结构关系,1倍数、倍数、几倍数,尤其要建立1倍数的概念。
4.辨析概念间的关系
教师将概念之间的关系分为相关联关系和不相关联关系,也可称为异同关系。辨析概念间的异同关系,可以避免混淆概念,有利于学生对概念的正确理解与建构,以及运用概念正确分析、判断与解决问题。
通过练习,学生知道两个量进行比较的时候,可以用相差关系进行比较,也可以用倍比关系进行比较,但它们表示的意义不一样。学生进一步明确“倍”的实质意义,“倍”表示的只是一种倍比关系,跟表示相差关系是有区别的,“倍数”是相对量,而不是绝对量。
(三)留白为“缺”——留给学生“生长”的“空间”
教师在课堂的最后可以留一个“缺口”,让学生有思考、讨论、交流、质疑问难的时间与空间,让学生能够循着这个“缺口”持续“生长”。
面对学生提出的问题,笔者没有直接回答对或者不对,而是留给学生一个思维的“缺口”,让学生自己画图思考、讨论交流。学生继而发现了一些“倍”的相关知识。以大数作为1倍,小数是不够1倍的,所以小数不能说是大数的几倍,这时怎么办?还能用“倍”来比较两者的关系吗?不能比了,又该怎样表示呢?为后续学习分数留下悬念。
“生长”的概念教学,是师生和谐发展的课堂,它以学生的经验为根,让学生在探究概念的过程中不断“生长”,并在课堂最后留给学生持续“生长”的“缺口”。

