算理贯通 理法相融——两位数加一位数（进位）学习新路径研究

□周小芳周 琪靳培英巩子坤

一、问题提出

两位数加一位数（不进位）要解决的关键问题是“算理贯通”“数位对齐”，并实现理法相融；两位数加一位数（进位）要解决的关键问题是“算理贯通”“进位”，并实现理法相融。在前文（见本刊2020年第11期《算理贯通理法相融——两位数加一位数（不进位）学习新路径研究》）中我们通过三次教学设计、二次教学实践，对比课堂教学中学生的表现、课后测试的结果，得到了两位数加一位数（不进位）优化的学习路径C。同样，要实现两位数加一位数（进位）算理贯通、理法相融的教学目标，也要设计合理的、具有逻辑关系的、层次递进的学习任务，这一系列学习任务就构成了两位数加一位数（进位）的学习路径。因而，为了得到这样的学习路径，本文同样研究了如前文中所述的4个问题。

我们同样采取行动研究法，在杭州一所普通小学的教师Z执教的甲、乙两班继续开展实证研究，研究设计、程序与有关的理论框架如前文。

二、学习路径D

（一）学习路径D呈现

教师Z在甲班实施的学习路径D如图1所示。

任务1、任务2都有现实背景。任务1是两位数加一位数（不进位），个位与个位相加不满十，不需要进位，重点解决“数位对齐”，这里意在帮助学生回忆、梳理已有的知识经验，为顺利迁移到两位数加一位数（进位）做铺垫。

任务2是两位数加一位数（进位），在学生已有经验的基础上，教师引导学生通过摆小棒这样直观的操作到有条理的语言表达，让学生经历从具体到抽象的过程，以此帮助学生理解算理，掌握算法。

（二）存在问题与原因分析

1.没有实现算理贯通

通过对课堂实录的分析，发现教师Z意在通过多种方式来表征算理。然而，事与愿违，没有实现算理的贯通，仅仅是多种表征的堆砌。

师：怎样用小棒表示24+8的计算过程？

生：先摆2捆，再摆4根，接着再摆8根。这8根中拿出6根和4根凑成10根，捆成一捆，结果是32。

师：先算什么？再算什么？

生：先算24+6=30，再算30+2=32。

师：还可以怎么算？

生：8根和4根先加起来是12根，12根加2捆，结果是32。

师：先算什么？再算什么？

生：先算4+8=12，再算20+12=32。

师：如果用计数器表示，你会吗？

生：先在十位上拨2颗算珠，再在个位上拨4颗算珠，最后在个位上再拨8颗算珠。

师：个位上的算珠超过了9怎么办？

生：在十位加1颗，个位只留2颗。

师：那就相当于先算什么？再算什么？

生：先算4+8=12，再算20+12=32。

师：那你们见过这两种算法吗？

师（指着竖式）：这是什么意思？

生：这是竖式。4加8等于12，个位满十要向十位进一，所以个位写2，向十位进一，十位上2加1等于3，结果是32。

师（指着方法24+10-2=32）：那这种方法你能看懂吗？

生：8+2等于10，10-2等于8。

师:我们把8化成10-2，之前我们学过了两位数加整十数，那么24+10等于34，然后34-2等于？

生：等于32。

由此可以看出，教师在教学过程中呈现的直观图仅仅是计算的结果，没有体现出计算的过程，也就是没有通过直观来凸显“进位”的过程，因而，也就没有留下直观的“进位”痕迹。如24+8=32，十位上由2变成3，这多出来的1个十，来源于何处，是如何得到的，直观图均没有体现（当然，教材中也没有出现）。没有直观的图，就不利于学生理解“满十进一”。

强调算法的多样性，本是一件好事，但是，本节课的主要目的是“理解算理，并实现不同表征的贯通”，因而，算法绝不是越多越好。教师使用了多种横式和竖式来表征24+8的计算过程，横式一种是4+8=12，20+12=32；另一种是24+6=30，30+2=32；还有一种是24+10-2=32。仅仅竖式和横式24+10-2=32教师就用了将近四分钟的时间来讲解。但是这些表征都没有很好地体现出“进位”，尤其24+10-2=32更是巧妙地避开了“进位”，与我们的教学目标背道而驰。教师追求多种方法的讲解，什么都想教给学生，结果反而使得计算方法杂乱无章、多而繁，由此造成直观表征与直观表征之间、直观表征和符号表征之间的割裂，没有实现表征的贯通，本质上也就没能够实现算理的有效贯通。

2.没有实现理法相融

师：现在我们就有四种方法来计算24+8，你们都学会了吗？

生：学会了。

师：接下来我要考考大家了。（接着学生开始做练习）

在教授完四种方法后，教学戛然而止，直接进入练习环节，教师并没有对两位数加一位数（进位）的算法进行一个总结、升华。虽然讲解了计算24+8的多种方法，但是这几种方法有没有相同点，有没有共性，学生不得而知。另外，教师在教学24+8时，在无任何铺垫的情况下出示了竖式，学生感到愕然。首先，教师要明白，竖式在一定程度上屏蔽了算理，不利于学生对算理本质的理解；其次，本次教学应该为后面“竖式”的学习做相应的铺垫，而不是简单苍白地呈现竖式。否则，后面学习两位数加两位数出现竖式时同样会使学生愕然。

（三）学习路径完善的建议

1.改变表征方式

要真正理解算理，就要促使多种直观表征之间、直观表征和符号表征之间相互贯通，实现表征一致性，进而实现优化。因此，无论是直观表征还是符号表征都要体现出进位，留下进位的痕迹，建议删去屏蔽了进位的横式和竖式。

2.增加关键提问

在学生掌握算理的基础上，为促使算理走向算法，就要及时提出关键问题：这些表征过程有何相同之处？在学生明确了要个位与个位对齐，满十进一后，再接着问：你能比较24+5和24+8的异同吗？

3.增加任务3

增加任务3：计算8+24，以此巩固算理、算法，并初步感受加法交换律。

三、重构的学习路径E

（一）学习路径E呈现

教师Z在乙班重构的学习路径E如图2所示。

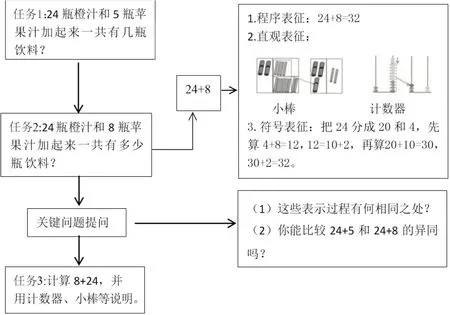
图2 学习路径E

相对于学习路径D，学习路径E有以下变化：

（1）实现多种表征的一致性。直观表征都留下了进位的痕迹，从进位前到进位后，整个计算过程一目了然。且直观表征与直观表征之间、直观表征与符号表征之间也相互贯通，相互呼应，有利于算理贯通。虽然学生在20以内的进位加法中学习了进位的概念，但那时的进位，所进上去的那位（十位）空无一物，无所依傍，也无所相加，因而，进上去的“1”显得孤零零的，学生对进位的感受并不明显；特别地，学生对8+7等于15已经朗朗上口，这进一步掩盖了进位的本质。所以，要浓墨重彩描述“进位”，凸显进位的过程，实现进位的一致与贯通。这恰恰是本堂课要突破的重点与难点。

（2）增加了思考问题。学生通过多种方法进行计算后，基本上已经掌握了算理，这时及时提出思考问题，引导学生寻找这些方法的相同之处，以促进算理有效贯通。同时，总结算法，使学生明白当个位相加满十时，需要向前进一位。

（3）增加了任务3，意在巩固算理，同时渗透加法交换律，使学生明白即便算式的形式改变了，但是本质没有变，依然要相同数位对齐，依然要满十进一；交换加数的位置，和不变。

（二）重构路径的效果分析

1.教学实况分析

（1）实现表征贯通。

师：用计数器怎样表示24+8的计算过程？

生：先在十位上画2颗算珠，在个位上画4颗算珠，因为是加8，所以在个位上再画8颗算珠。（学生边说，教师边在黑板上操作，画出直观图）

师：这样个位上的算珠有多少颗？

生：12颗。

师：我们知道计数器的个位上最多只有几颗算珠？

生：9颗。

师：也就是说个位上的算珠数已经超过了？

生：超过了9。

师：那怎么办呢？

生：满十进一，要从12颗中拿出10颗放在十位上，也就是个位上的10颗变成十位上的1颗。

师：那个位上还有几颗？

生：还有2颗。

师：所以结果是？

生：32。

（学生边说，教师边在黑板上操作，画出如图3所示的直观图，留下思考的痕迹）

师：那么用摆小棒的方法怎么表示呢？

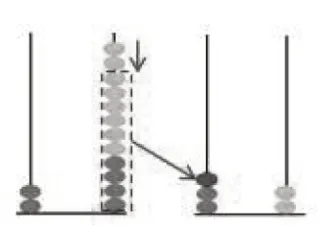
图3

生：先摆2捆，再摆4根，加8，就再摆8根。

师：那右边有几根？

生：有12根。

师：可以变一变这个形式吗？

生：从右边拿10根捆成1捆，放在左边。

师：那左边现在有几捆了？

生：有3捆。

师：这一捆哪里得到的？

生：从右边拿出的10根捆成了1捆。

师：那右边还剩多少？

生：还剩2根。

师：所以结果是？

生：32。

（学生边说，教师边在黑板上操作，画出如图4所示的直观图；该图事实上是为竖式的出现做好铺垫）

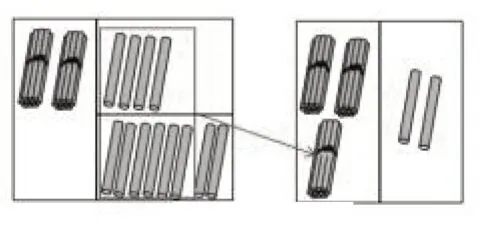
图4

（2）实现理法相融。

师：这两种方法得出的计算结果一样吗？

生：一样，都是32。

师：用的工具一样吗？

生：不一样。

师：为什么用的工具不一样，而结果会一样呢？

生：计算过程一样，都是先算个位，再算十位。

师：还有呢？

生：都是满十进一。

师：都是哪里满十进一？

生：都是个位满十，向十位进一。

师：个位怎么计算的？

生：4+8=12。

师：满十进一的十从哪里来的？

生：从12中拿出一个10。

师：也就是把12分成10和2。然后把拿出来的这个十加到哪一位上？

生：十位。

师：也就是说十位上要加一个十，算式是？

生：20+10=30。

师：个位上还剩几？

生：还剩2。

师：所以十位上和个位上的数加起来是？

生：30+2=32。

师：老师想问问大家，算式24+8和24+5有什么不一样吗？

生：第一个加数都一样，都是24，第二个加数一个是8，一个是5。

生:24+5个位上的数相加没有满十，24+8个位上的数相加满十了，要向前进一位。

师：对，满十要进一。你会计算8+24吗？

生：会，等于32。

师：谁来说说是怎么计算的？

生：因为24+8等于32，8+24也等于32，它们都是一样的数，只不过交换了一下加数的位置，结果还是一样的。

师：如果让你用这些方法表示，你会吗？怎么表示？（教师指向直观图）

生：先画出数字8，再画出数字24。

师：计算方法是？

生：先算个位，个位满十要向十位进一。

通过以上教学过程，最终使学生明白，两位数加一位数，要先算个位，当个位上的数相加满十时，需要进位，满十进一。在此过程中，边回顾算理，边让算理水到渠成地走向算法。

2.课后测试结果比较

为了检测路径D、E的实施效果，我们设计了2道题目，两次教学前后分别对甲、乙两班的学生实施了前后测（表1、表2），以此考查学生掌握算理的情况。

先列式计算，然后用尽可能多的方法，如文字解释、画直观图、算式表示等来说明你的计算方法是合理的，说明得越详细越好[1]。

（1）小明上午买了28瓶矿泉水，下午又买了4瓶，小明今天一共买了几瓶矿泉水？

（2）小明上午花了26元钱，下午花了6元钱，小明今天一共花了几元钱？

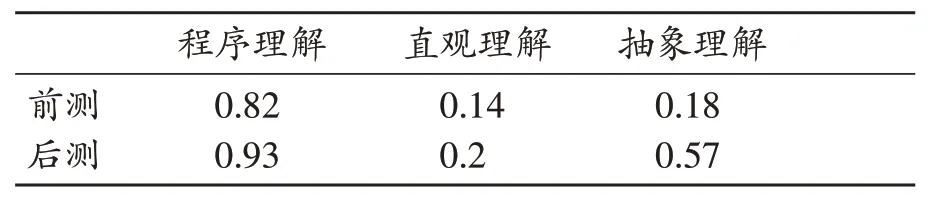
表1 第一次教学甲班前后测不同理解类型的平均分

由表1可以看出，在三种理解类型上，后测的数据高于前测，尤其是程序理解和抽象理解。后测中程序理解的平均分是0.93，也就是说绝大部分学生可以正确地计算两位数加一位数（进位）的得数；直观理解的平均分是0.2，相对来说增长较少，说明大部分学生还不会画直观图。

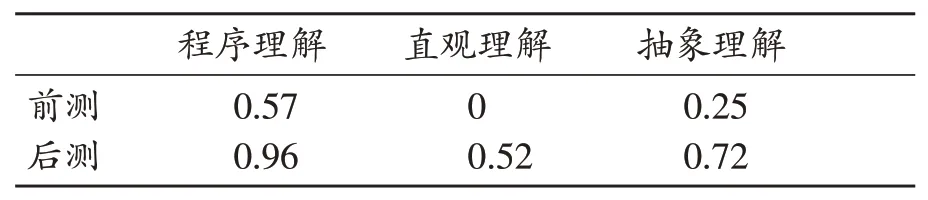
表2 第二次教学乙班前后测不同理解类型的平均分

由表2可以看出，后测数据中，程序理解的平均分是0.96，即绝大部分学生能够准确计算出得数，直观理解的平均分是0.52，即有一半的学生会画直观图，且这个数据大幅度高于前测，抽象理解的平均分是0.72，即有大部分学生会语言表述计算过程。整体上说，在三种理解类型上，后测的数据要大幅度高于前测，也就是说，实施学习路径E后，教学取得了较好的效果，说明这一路径得到了优化。

3.问题与改进建议

（1）任务3的进一步完善。

教师通过引导学生比较24+5和24+8的异同后，让学生计算8+24，给学生提供时间与空间，以巩固算理、算法；由于算理不可能一次掌握，所以，此处给学生提供反思、巩固的机会就显得十分必要。同时，让学生比较8+24和24+8的异同，以此感悟交换律。

（2）竖式再次出现。

尽管我们强调了“竖式”不利于算理的贯通，甚而屏蔽了算理，但是教师Z没有采纳这一建议。在她看来，也许竖式更利于计算。

四、结论与建议

（一）学习路径的建议

学习路径设计的重点是遵循程序性知识学习的心理路径，设计层层递进的学习任务[2]。通过对学习路径D、E的实践、分析、反思与批判，从促进学生理解算理的视角出发，我们建议两位数加一位数（进位）的学习路径可构建如下（图5）。

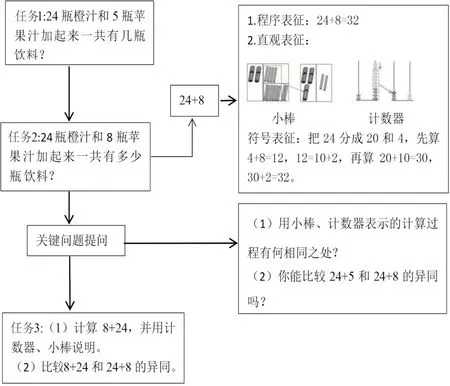
图5 学习路径F

（二）算理贯通的重点是促使多种表征贯通

调查表明，大部分学生“都知道怎样算，但是对于这样算的道理却知之甚少”。[3]

也就是说，学生只掌握了算法，并不理解算理。而各种表征就是沟通算理与算法之间的桥梁，一头连接着隐性而抽象的算理，另一头连着显性而具体的算法。因此，学生能否理解算理，能否灵活运用算法，各种表征的呈现就显得至关重要。

（三）理法相融的重点是促使算理走向算法

没有算理的理论支撑，就不能提供正确的思考方向，从而容易导致计算的不合理性和错误率，离开算法的提炼概括，算理的存在也是毫无意义的[4]。也就是说，算法中蕴含着算理，算理解释着算法，促使算理走向算法，实现理法相融至关重要。