椭圆曲线y2=(x+a)(x2-ax+p)的大整数点

冉银霞

（陇南师范高等专科学校数信学院，甘肃，成县742500）

0 引 言

由于椭圆曲线理论集数论、代数、几何和复变函数论为一体，它具有很强的实用性和应用性。从丢番图方程到密码学，再到理论物理中的弦理论，都可以看到它的身影。尤其椭圆曲线理论在关于素性检测、大数分解以及离散对数中的算法更使得椭圆曲线密码(ECC)在近几十年里成为密码领域流行的标准术语，并得到了十分广泛的应用。著名的费马大定理应用了大量极为深奥的椭圆曲线理论而彻底解决。21世纪7 个千禧难题之一的BSD猜想，就是与椭圆曲线有理点有关的极具挑战性的难题。同余数问题的本质也与椭圆曲线的算术紧密相关。特别地，其本质是椭圆曲线的BSD猜想和Goldfeld猜想。近50年来，确定椭圆曲线的整点问题就显得非常重要，也是数论和算术代数几何中的重要问题[1-3]。

早在1987年，D.Zagier 在文献[4]中询问椭圆曲线y2=x3+ 27x-62的最大整数点是否为(28844402，154914585540)。它是椭圆曲线

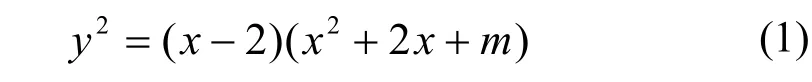
中的一种。由于这是一类典型的秩等于1且有大整数点的一种椭圆曲线，所以该问题对于讨论椭圆曲线的算术性质有着重要的意义。因此，椭圆曲线整点问题对于在不同情况下构造合适的椭圆曲线函数具有重要的理论意义及应用前景。然而寻找其较大正整数解非常困难，其耗费的时间可以用正整数的指数幂来计算。这样一来针对不同的椭圆曲线解决的方法也有待探讨与提高。且上述椭圆曲线的研究成果主要结果集中在：当m=7，15，18，23,31，43，139，m=36s2-5，s为正奇数，且6s2－1，12s2+1均为素数，m=4p- 8=q+ 1,或m=2p- 8=q+1且p≡/ 1 (mod 8)时，已经找到对应椭圆曲线全部整数点[4-13]。

本文运用初等方法，证明了下面的定理和推论。

1 主要引理

2 定理的证明

于是由引理1知(26)有整数解的充要条件是a只有形如8 1k± 的素因子，或a含有8 3k± 的素因子的个数为偶数。

(VII)当d=8p时，可令

3 推论的证明

4 结论

文中运用初等方法，主要通过构造二元四次方程，利用奇偶分析、同余及模p的Legendre符号的性质，巧妙地解决了一族椭圆曲线整点的求解问题，得到的结论填充了这类椭圆曲线研究成果的空白。其求解方法可应用于其它类似方程的研究。找到的这族具有大整数点的椭圆曲线有很大的理论价值与很好的应用前景。