基于信息保真度的最优信息传输

马 卓, 侯志相, 王世强

(吉林省军区 数据信息室, 长春 130033)

0 引 言

在含噪信道中如何有效地传输信息是信息和通信理论及工程应用中的关键性问题。互信息是这一领域的核心概念[1], 它度量了信息发送端经过信道, 向接收端传递的有效信息。从信道编码理论中知道, 由于噪声的干扰, 信道的信息速率不可能无限大, 而是受限于互信息的最大值也即“信道容量”[2]。为提高信息速率, 人们会在发送端采用信道编码[3-7], 以优化消息的码元分布、 接近甚至达到信道容量。由于信息传输模型的复杂性, 信息传输的优化也是比较困难的问题。例如最简单的语音信号模型是马尔科夫过程, 即使信道噪声是时不变的, 但接收端收到的含噪信号的统计行为也往往是非马尔科夫的。因此发送端与接收端之间的互信息将是非常复杂的函数[8-9], 优化传输码元分布以达到信道容量也是非常困难的。

为了克服这一困难, 笔者提出了新的信息传输的保真度概念, 用以度量被信道噪声污染后有效信息的可恢复程度。信息保真度与互信息既有区别又相互联系。互信息是两个随机变量的联合分布对两个边缘分布乘积(也即相互独立的联合分布)的相对熵[10], 表示随机变量的关联程度。信息保真度是对称化的相对熵[11-14], 既包含了互信息, 又包含了另一个新的关联度量----在随机性影响下随机变量的误差信息, 这可以更全面地表示噪声对于信息传输的影响程度。另一方面, 笔者提出的信息保真度的概念既不依赖于具体的信息恢复方法, 又可以度量信息恢复方法如极大似然法或极大后验概率法的误差概率下界。相应地, 笔者提出了使信息保真度最大化的最优信息传输问题。相较于使互信息最大的传输最优化问题, 复杂模型的基于信息保真度的优化可以有更为简单的形式。

1 噪声下的信息恢复

假设信息发送端依据(先验)概率PS(S)发送消息S∈S至接收端, 其中S是所有可能的消息S的集合。相应地, 接收到的消息记为X∈X, 其中X是所有可能的接收消息X的集合。由于受信道噪声干扰, 接收消息X未必正好是发送的消息S(集合X也未必等于集合S)； 而是存在随机映射S →X, 其依照条件概率PX|S(X|S)将每条发送的消息S映射至每条收到的消息X。这里, 条件概率PX|S(X|S)表示信道的性质。为方便起见, 假设信道是时不变的, 相应地条件概率PX|S(X|S)也是时不变的。另外, 还假设发送消息的概率PS(S)和条件概率PX|S(X|S)都是已知的。

如果通过收到的消息X恢复发送的消息S, 可采用一定的信息恢复方法, 其中两种代表性的方法分别为极大似然法和极大后验概率法[2]。这两种方法可以统一地写为下面形式： 当收到消息X, 选取消息S∈S使

fX(S,S′)=lX(S,S′)-γ(S,S′)>0,S′≠S

(1)

2 信息保真度

从信息论的角度看, 式(1)中的f可以度量消息的保真度, 也即有效信息可被恢复的程度。常规看, 如果给定消息的先验分布PS, 当发送和收到的消息分别为S、X时,fX(S,S′)≤0说明消息S完全不能恢复。另一方面, 当fX(S,S′)在其正值区间内越来越大, 说明S的后验概率PS|X(S|X)也会相对其他S′≠S的后验概率变大, 因此S更容易被恢复。反之, 随着fX(S,S′)减小,S可恢复程度随之变小。为更清楚地说明f是消息保真度的度量, 可将式(1)重新写为如下形式

fX(S,S′)=i(S,X)-i(S′,X)

(2)

据此, 可用平均信息保真度(以下简称保真度)在整体上度量有效信息可被恢复的程度

(3)

3 信息保真度与信息恢复误差

当发送和收到的消息分别为S、X时, 若S是满足式(1)的极大似然估计或极大后验概率估计, 则原消息S就被正确地恢复。否则, 如果存在极大似然估计或极大后验概率估计S′≠S, 则原消息S没有被恢复, 所用的信息恢复方法产生了误差。

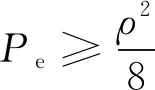
(4)

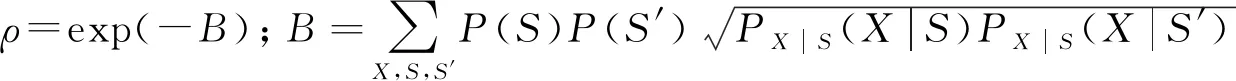
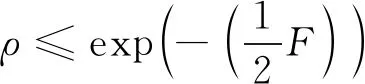
(5)

则由式(4)、 式(5), 可得到误差概率Pe的一个下界可以用保真度F表示为

(6)

式(6)印证了随着保真度F增加, 信息恢复的误差概率下界可以随之减少, 相应地越多的有效信息可以被恢复。

4 表示最大信息保真度意义下的最优信息传输

在工程应用中, 人们关心互信息最大化问题的原因是： 1) 在时不变信道条件下, 互信息I在所有可能的信道编码分布PS上有唯一最大值； 2) 这个互信息I的最大值对应有效信息传输速率的上界, 也即信道容量。在最大互信息I意义下得到的(唯一)最优信道消息(编码)分布P*可保证在最快的速率下传输信息。

另一方面, 若更关心从含噪传输中最大程度地恢复有效信息, 则在信道条件不变的前提下找到最优消息分布使保真度最大化。为了得出这一点, 将式(3)中的F改写为关于PS的二次型形式

(7)

其中

是对称化相对熵。K也是式(7)中二次型的海森(Hessian)矩阵, 表示了信道的统计性质。如果信道是时不变的,K也是时不变的。需要强调的是, 对称化相对熵是概率分布间的伪距离函数。这是因为K满足[14]： 1) 非负性， 即K(S,S′)≥0, 等号成立当且仅当S=S′； 2) 对称性， 即K(S,S′)=K(S′,S)。

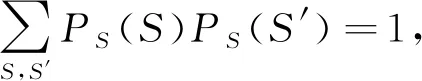
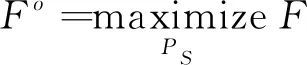
(8)

即在假设信道时不变下, 求取最优的消息分布Po, 使保真度F最大。容易知道Po仅依赖于K, 相应地最大保真度Fo也仅依赖于K, 因此类似于信道容量(互信息最大值),Fo也可作为信道特性的表示, 度量信道传输有效信息的最大程度。

5 实 例

为具体说明最大信息保真度的意义, 以二元无记忆信道为例, 分别计算其信道容量以及最大保真度。假设信源发送的消息S为平稳的马尔科夫序列。码元s=0,1之间的跃迁概率可由如下的马尔科夫矩阵表示

(10)

(11)

其中e0,e1分别代表码元s=0和s=1的误码概率。给定码元跃迁概率q时, 发送和收到的码元s和x的互信息(率)为

(12)

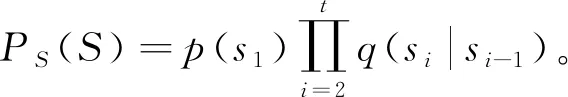
(13)

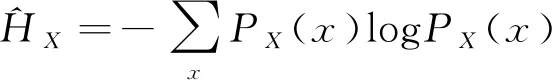
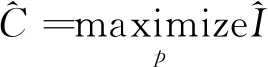
(14)

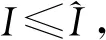
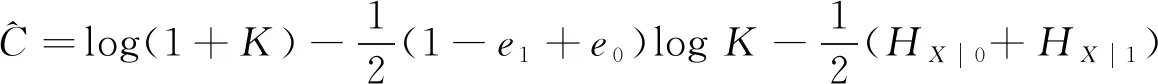
(15)

其中

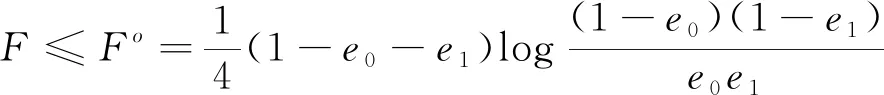
(16)

图1 二元无记忆信道的信道容量、 最大信息保真度及对应于最大信息保真度的互信息、随误码概率e0和e1的变化情况

图2 对于不同的误码概率， 互信息随着最大保真度的变化情况

6 结 语

笔者提出的信道信息保真度与互信息有着紧密的联系, 它表示了信道传输信息的可恢复程度。最大信息保真度同信道容量一样表示了信道特征。笔者通过例子说明, 使信息保真度最大化可以增加信道传输的有效信息并降低信息恢复误差。最大信息保真度计算上的便利性也表明了信息保真度与相应的最优信息传输问题有着良好的应用前景。