边缘导向的非局部均值图像滤波

傅 博, 吴越楚, 王丽妍, 王瑞子

(辽宁师范大学 计算机与信息技术学院, 辽宁 大连 116081)

0 引 言

目前数字图像已经是日常生活中不可或缺的信息载体, 并在科技发展及普及过程中占有举足轻重地位。数字图像处理是信号处理、 人工智能、 模式识别、 优化理论等交叉学科和技术。涵盖了图像恢复、 增强、 分割和分类等领域。在低级视觉应用中, 图像去噪是一个存在已久、 具有极高实用价值。对图像去噪, 其本质上属于图像恢复的一种。其旨在将受损图像恢复为最优的潜在图像。在实际应用中, 图像由于各种原因均有可能携带噪声, 比如转成数字图像过程中产生的误差、 空气波动或是由每个传感器中光子计数过程的随机性造成的。但由于采集设备可能长期暴露在诸如工地、 草场和广场等光线条件复杂的环境下, 存在被光线变换、 雨雪、 天体放电等干扰的可能, 在极端情况下, 极有可能产生高强度噪声污染的图像。从噪声的概率分布情况看, 图像中的噪声可分为高斯、 瑞利、 伽马、 指数和均匀噪声等。高斯噪声是指概率密度函数服从高斯分布(即正态分布)的一类噪声。由于其往往是叠加在图像上的随机噪声, 因此会严重影响图像质量, 降低图像的观赏程度。同时, 图像的内容因噪声退化而不再连续变化, 进而导致图像的本质特征发生改变, 使图像增强、 识别、 分类等高级视觉任务变得更加困难。由此可见, 图像去噪技术不仅可以提高图像的视觉质感, 达到赏心悦目的感觉, 也是现代计算机视觉分析任务的基础。

图像去噪方法目前主要包括稀疏模型[1-3]、 马尔可夫随机场模型[4-6]、 梯度模型[7-8]与信号模型。信号模型包含空间域处理方法与频域处理方法。空间域处理方法直接在图像所在的二维空间进行处理, 即直接对每一像素的灰度值进行处理, 包括均值、 高斯、 形态学、 局部和非局部滤波等。频率域处理方法主要有维纳滤波和小波阈值收缩等。其中局部均值是一种直接在空间域上对图像进行平滑处理的方法。在图像上对待处理的像素给定一个模板, 该模板包括了其周围的临近像素。将模板中的全体像素的均值替代原像素值。该方法的优点便于实现, 计算速度快, 结果也比较令人满意。

事实上, 很多图像都具有一定的自相似性质, 比如纹理图像。具体表现在不同位置的像素之间也可能有很强的相关性。因此, 在图像中的某一像素点的一定邻域范围, 就可以代表该像素点的结构特征。这意味着一幅图像就是由这些以像素点为中心的特征图像块组成。当从图像中选取一个像素点时, 分析其邻域所包含的图像信息, 便可以在该幅图像中找到很多与之相似的结构。如果用相似的结构替换被噪声污染的结构, 所得到的图像效果将强于单纯用局部均值替换噪声点的效果。

基于上述原理, 笔者提出了一种边缘导向的非局部图像去噪方法。首先, 对高强度高斯噪声污染的图像采用二阶差分Sobel算子抽取边缘； 其次, 将边缘信息与原有的噪声图像共同构建一个非局部协同滤波框架； 最后, 在修复过程中, 边缘信息参与噪声图像的修复, 使去噪图像获取更多的边缘纹理信息。

1 相关工作

对目前较为常见的叠加性噪声而言, 噪声图像的生成通常遵循如下模型

y=x+n

(1)

其中x为潜在图像,y为受损图像,n为噪声。n的类型分为多种, 例如高斯、 均匀和椒盐噪声。由于噪声类型的不同, 导致去噪任务拥有一定的挑战性。根据贝叶斯理论, 求解最优潜在图像等价于求解最大后验概率估计问题

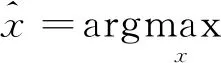
(2)

其中logp(x|y)为已知观测值y的对数似然函数, logp(x)为x的对数先验分布函数。令f(x,y)=-logp(y|x),g(x)=(1/λ)logp(x), 式(2)可定义为

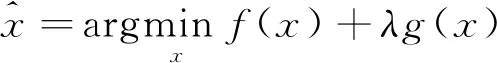
(3)

其中f(x,y)为数据保真项,g(x)为正则项,λ为正则项系数。根据式(3), 不难得出图像去噪问题的优化模型

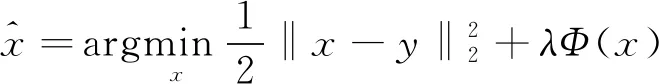
(4)

其中Φ(x)为正则项,λ为正则项系数。根据优化理论的梯度下降算法[9], 可得出其问题的迭代求解算法

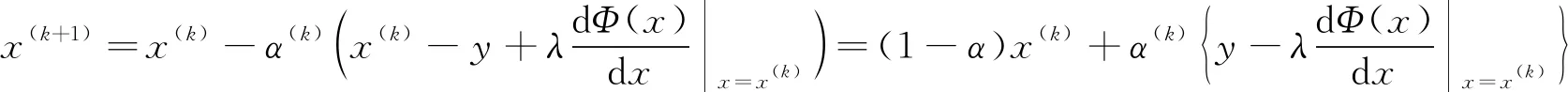
(5)

其中α(k)为每次迭代的学习率。该方法的最终效果取决于两点: 一是筛选合适的学习率; 二是寻找合适的正则项。但这两者在实际中是较难获取的, 通常需要相关人员拥有大量的先验知识。虽然基于稀疏模型的方法[1-3]提供了相应的正则项, 但由于保稀疏所用到l0范数会使式(4)变为非凸问题, 导致其难以求解。因此, 在优化模型外, 同样衍生出很多新颖的方法, 比如基于马尔可夫随机场的去噪方法[4-6], 基于梯度去噪方法[7-8]等。但上述两种方法需要估计图像中潜在分布以及梯度计算, 同样需要极为复杂模型, 加大了程序运行的时空开销。基于上述理论不足, 笔者通过信号角度, 以空间域滤波理论为基础提出一种基于导向图的非局部去噪方法。

2 边缘导向的非局部均值图像滤波算法

2.1 边缘导向的非局部均值滤波器构建

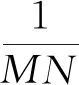
为了在去噪过程中尽可能地保留边缘信息, 边缘保留滤波器成为了诸多学者关注的焦点, 导向滤波器[20]则是其中的一种。导向滤波器除了需要输入图像外, 还需要一个边缘导向图。通过相关的边缘导向图与特点的图像处理任务结合可获取不同的效果。若导向图为暗通道图像, 则导向滤波会大大提升去噪能力； 若导向图与输入图像一致, 则导向滤波能拥有一定的去噪能力。为了解释这一现象, 可以从图像梯度角度进行考虑： 在自然图像中, 图像的平滑区域的像素变化率较小, 根据离散信号的差分理论不难得出其梯度较小。图像的边缘区域像素变化率较大, 则其梯度较大。同理, 噪声周围的梯度变化亦会较大, 不难得出噪声位置四周的梯度大体相似。而边缘所在位置出现的梯度阶跃最大方向是沿着边缘的法线方向, 在滤波时, 导向图可以预测待去噪图像信息属于边缘或平面, 因此, 输入图像就可以利用这些信息进行滤波。需要注意的是只有当导向图和待处理图像之间属于线性导向关系才有意义。为了更好地解释导向图在非局部均值滤波中的积极影响, 首先对非局部均值滤波理论进行分析。

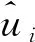
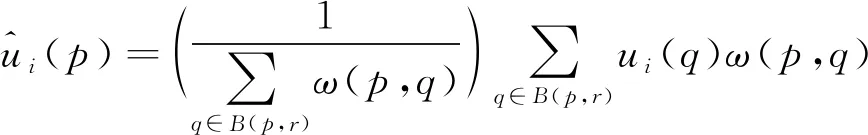
(6)

其中i=1,2,3和B(p,r)分别表示以p为中心、 大小为(2r+1)×(2r+1)像素的邻域。由于计算限制, 该研究区域仅限于固定大小的正方形邻域。当σ值较小或中等时, 窗口大小为21×21; 当σ值较大时, 由于需要寻找更多的相似像素以进一步降低噪声, 窗口大小可增加至35×35。权重w(p,q)的值取决于分别以p和q为中心、 半径为f的正方形邻域的欧氏距离的平方, 邻域半径f固定为1。设欧氏距离平方为d2, 则

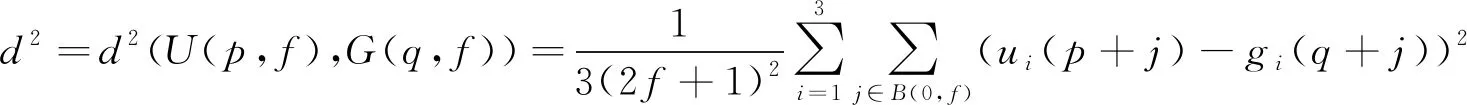
(7)

其中U(q,f)为输入的噪声图像,G(q,f)为导向图。

滤波器权重w(p,q)满足指数衰减, 其计算方式为

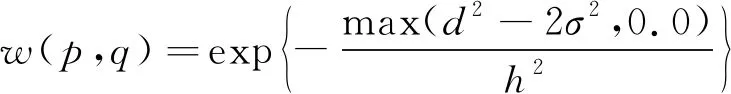
(8)

其中σ为噪声的标准偏差,h为根据σ值设置的滤波参数。设置权重函数是为了将相似的块更好地平均噪声。平方距离小于2σ2的块被设置为1, 而更大的距离会随着指数核而迅速减小。

参考像素p在平均值中的权重被设置为邻域B(p,r)中权重的最大值。此设置避免了参考点在平均值中的过度权重。否则,w(p,q)为1, 并且需要更大的p值以确保降噪。通过应用上述均值化过程, 非局部均值框架可以确保每个噪声像素p处得到有效恢复。

2.2 边缘导向的非局部均值图像滤波算法

为了进一步加强图像去噪能力以及丰富图像边缘信息与纹理信息。笔者通过Sobel算子提取图像边缘。设x方向的Sobel算子为gx,y方向的Sobel算子为gy, 则边缘提取过程为

G=I⊗gx+I⊗gy

(9)

其中G为边缘图像,I为经过一次非局部均值后的图像, ⊗为卷积算子。

由于边缘图像中存在若干干扰信息, 因此需要通过阈值分割过滤掉部分干扰信息。为了使结果趋于稳定, 采用大津法进行阈值分割。综上所述, 提出的导向非局部均值去噪算法的大致过程如算法1所示。

算法1 GuideNLM Denoise

Input:Inoise,h, neightSize, searchSize

Output:Idenoise

1) out=GuideNLM(Inoise,Inoise,h, neightSize, searchSize)

2)G=out⊗gx+out⊗gy

3)G=OSTU(G)

4)Idenoise=GuideNLM(out,G,h/2,neightSize, searchSize)

其中neightSize为邻域大小； searchSize为搜索窗口大小； GuideNLM(·)为导向非局部均值滤波操作, 参数自左向右为噪声图像、 导向图像、 平滑系数、 邻域大小以及搜索窗口大小。当导向图与输入图像一致时, 其效果等价于传统的非局部均值滤波操作。

3 实验与结果分析

实验操作系统为Windows 10, 平台为Matlab R2018a。为验证导向非局部均值滤波的去噪能力, 对Lenna图加入强度为70的高斯噪声进行测试。其中算法的邻域窗口为3×3, 搜索窗口为21×21, 平滑系数为3, 测试效果如图1所示。

a 清晰图像 b 噪声强度为70的受损图像 c 经过一次非局部均值滤波操作后的图像 d c的边缘提取图像 e 以d为导向图对c进行的导向非局部均值滤波操作后的图像

为了验证导向非局部均值滤波的优点, 依然以Lenna图作为测试图像, 对噪声强度为35～70 dB的情况进行了进一步统计, 其量化结果如表1所示。

表1 噪声强度为35～70 dB的量化结果

为进一步突出导向非局部均值滤波的优越性, 额外选用3张不同的测试图像, 在噪声强度为50的情况下, 通过峰值信噪比(PSNR: Peak Signal-to-Noise Ratio)与结构相似度(SSIM： Structural Similarity)对实际结果进行量化, 其量化结果如表2所示, 图2为去噪效果图。

a 噪声图像 b 传统NLM去噪图像 c 边缘图像 d 导向NLM去噪图像

综上所述, 传统的非局部均值滤波与以边缘图像为导向图的导向非局部均值滤波相比, 后者明显优于前者, 因此以边缘图像为导向图的导向非局部均值滤波方式更符合理想的去噪滤波器, 更适用于高强度噪声的去除。

表2 相同噪声不同测试图像的量化结果一览表

4 结 语

笔者针对传统局部滤波和非局部滤波对于高强度高斯噪声干扰噪声图像, 去噪后边缘信息修复能力弱的问题, 通过引入边缘信息, 并构建非局部协同滤波, 有效地将边缘信息引入到噪声图像的修复过程中。最后通过实验, 证明了以边缘图像为导向图的导向非局部均值滤波既可以有效过滤掉噪声, 而且还能很好地保护图像细节信息, 对高强度噪声图像的还原度很高。