基于极限学习机的未校准图像视觉伺服控制

张振国, 任晓琳, 高润泽, 刘克平

(长春工业大学 电气与电子工程学院, 长春 130012)

0 引 言

视觉反馈信号用于作机器人工业中, 尤其是在非结构化环境中实现定位或运动控制[1-2]。视觉伺服利用目标对象的视觉特征信息计算机器人控制律, 从而收敛到允许的误差域。根据视觉反馈返回信号值的表示形式是3D空间坐标值还是图像特征, 可分为基于位置的视觉伺服(PBVS: Position-Based Visual Servoing)[3-4]、 基于图像的视觉伺服(IBVS: Image-Based Visual Servoing)[5-7]和混合视觉伺服控制系统[8-9]。IBVS不需要场景模型或摄像机/机器人校准[10-11]。其使用参数估计识别未知的相机参数, 然后基于识别出的雅可比矩阵设计控制器以获得最佳性能[12]。

对运动学非标定视觉伺服, 其控制律的设计最关注交互作用矩阵问题。运行过程不仅包含模型和参数的不确定性, 而且还受到噪声和外部干扰的影响。支持向量回归(SVR: Support Vector Regression)将关节角的每个特征分量非线性地映射到图像特征空间, 为每个关节角构造一个支持向量回归机, 然后获得图像雅可比矩阵的表达式[13-14]。文献[15]提出了基于神经强化学习控制器和传统的IBVS控制器, 为视觉伺服系统开发了一种切换控制策略, 该算法无需求解图像交互矩阵的伪逆。

为了避免直接求解图像雅可比矩阵的逆问题, 笔者提出了一种使用增量式极限学习机(I-ELM: Incremental Extreme Learning Machine)的设计方法, 该方法具有鲁棒性且可以解决图像奇异问题, 并采用了一种改进的自适应控制器, 以更短的收敛时间显示出更有效的速度曲线。

1 机器人执行器IBVS原则

在研究中, 安装在机器人末端执行器上的摄像机随机器人一起移动。视觉伺服控制的主要目的是通过机器人的关节动作将机器人的末端执行器与摄像机一起朝期望的图像特征移动。以图像特征作为控制目标在时刻k图像空间误差可表示为

e(k)=S(k)-S*

(1)

其中S(k)=[S1(k),…,Sm(k)]T是在时刻k的图像特征向量,m是图像特征的总数,S*是期望的特征向量。

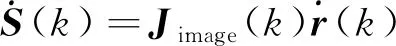
(2)

其中Jimage(k)为图像的雅可比矩阵, 定义如下

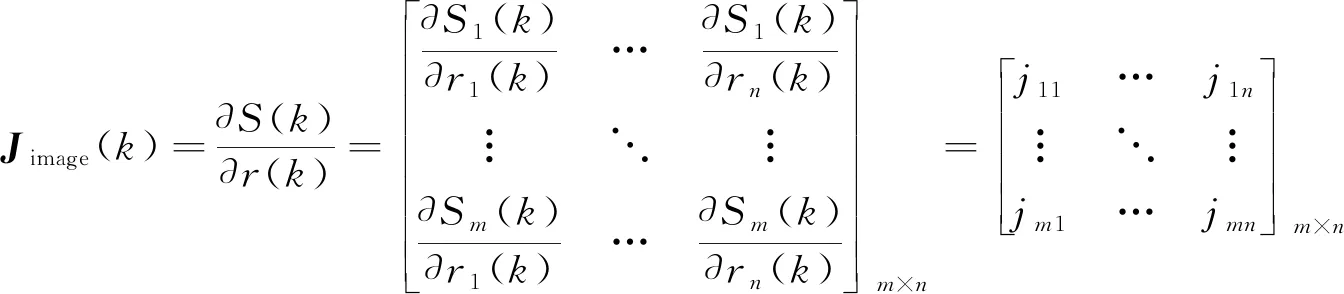
(3)

为了将机器人从当前姿势驱动到所需姿势, 最有效的方法是采用比例控制

(4)

2 基于图像的视觉伺服控制

根据式(4)可知, 该速度控制器的性能取决于伪逆和增益。由于配置可能会导致相机校准参数或功能噪声的奇异性和错误, 因此使用图像雅可比矩阵计算伪逆并不容易。这些干扰也会影响速度曲线的抖动, 因此使用固定增益是不合适的。基于以上考虑, 笔者使用I-ELM和平滑增益解决这些问题。

2.1 IELM函数近似方法

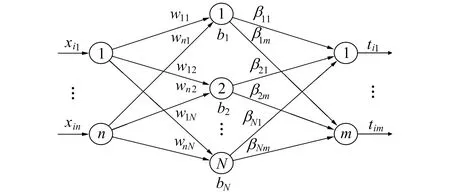
图1 ELM的结构

极限学习机(ELM: Extreme Learning Machine)是一种简单有效的单隐层前馈神经网络学习算法, 其结构如图1所示, 对N个不同样本(xi,ti), 其中xi=[xi1,xi2,…,xin]T∈Rn以及ti=[ti1,ti2,…,tim]T∈Rm, ELM对广义的单隐层前馈神经网络的输出函数是

(5)

其中ωi∈Rn是第i个连接输入层到隐含层的权值向量,βi=[βi1,βi2,…,βim]T∈Rm是第i个连接隐含层到输出层的权值向量,bi∈R是第i个隐含层的偏差,g(·)是激活函数。

由于得到理想的神经元数量很困难, 为解决该问题, Dong等[7]提出了增量式极限学习机, 增量式极限学习机的原理如下： 给定一个训练集合X包含N个不同的训练样本(xi,ti)、 隐含层函数g(x)以及隐含层最大的连接数Lmax, 根据用户期望的训练误差1次增加1个节点, 具体步骤如下。

1) 初始化协相关矩阵。设定神经网络残差矩阵E=T, 以及初始隐含层节点L=0。

2) 决定是否存在网络最大的隐含层节点Lmax。对隐层L或网络的均方根误差是否小于所需的训练误差ε; 如果是, 则极限学习机学习结束; 否则， 执行将继续。

3) 给隐含层节点标号L=L+1。

4) 计算添加到网络的输出权重并更新网络的残差矩阵。 然后, 跳转到2)后继续。

对I-ELM的研究是用于函数的逼近, 将图像特征的元素作为输入, 而输出则是图像雅可比矩阵的伪逆的每个元素。

2.2 速度控制器

在运动学视觉伺服控制中, 基于式(4)的速度控制器采用固定增益, 该增益确定收敛时间和速度曲线。为了快速收敛, 笔者采用非齐次的一阶微分方程以保证连续性[9], 微分方程式为

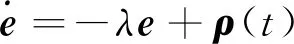
(6)

其中非均匀项ρ(t)表示为

ρ(t)=e-μt(H(0)+λe(0))

(7)

为保证短暂的持续响应, 则必须μ>λ, 在实验中采用μ=10λ。改进的控制器根据式(5)～式(7)重新写为

(8)

其次, 为了在系统的实现中获得快速运动, 速度控制器式(8)引入了一个自适应因子, 表示如下

(9)

其中α(t)=(1-a)/(1-at+1)是自适应因子,a是影响因子, 0

2.3 视觉伺服控制策略

笔者提出控制方法的框架如图2所示。首先利用I-ELM近似图像雅可比矩阵的伪逆, 实现视觉空间与运动空间之间的非线性映射, 改进后的速度控制器可以快速收敛。最后通过控制律将机器人的末端从初始位置驱动到所需位置。

图2 提出方法的结构框图

3 仿真实验

在仿真实验中将模拟摄像机安装在六自由度的Puma560机器人的末端执行器上, 目标是由4个圆形特征点组成的静态目标。在仿真中笔者以高斯噪声作为干扰, 评估目标是IBVS及其方法的测试轨迹和速度性能。

摄像机解析度为800×800 像素, 主点的坐标是(400,400), 焦距为8 mm, 手动调整比例增益λ=0.5。所需的图像特征矩阵如下

(10)

I-ELM的数据集是通过IBVS系统获得的。I-ELM根据210个不同初始姿势得到的数据训练, 隐藏节点的数量是136, 仿真实验分两种情况。

基于高斯噪声实验在30～40 s和80～90 s的仿真中引入10倍的原始噪声。在图3中, IBVS方法的特征轨迹被噪声扭曲; 在图4中, I-ELM方法在运动中有轻微的颤动。

图3 IBVS方法的特征轨迹 图4 I-ELM方法的特征轨迹

图5为IBVS方法控制下的末端执行器轨迹。图6为I-ELM方法下的末端执行器轨迹, 可以看出末端执行器轨迹都在突然的噪声下产生一定的振动, 但显然后者曲线更平滑。在IBVS方法控制下的末端执行器的速度如图7所示, 在I-ELM方法下的末端执行器的速度如图8所示, 通过图7, 图8对比可以看出, 笔者提出的方法表现出更好的运动效果和较小的振动, 且保持了较高的收敛速度。

图5 IBVS方法的末端执行器轨迹 图6 I-ELM方法的末端执行器轨迹

图7 IBVS方法的末端执行器速度 图8 I-ELM方法的末端执行器速度

4 结 语

笔者使用I-ELM研究图像雅可比矩阵的伪逆, 避免了矩阵的奇异性, 并且其具有更好的特征轨迹性能。同时, 使用了自适应因子调整速度控制器的收敛速度。该系统针对带有手眼摄像头的Puma560机器人进行了仿真, 与IBVS相比该算法的性能更理想。