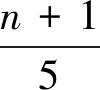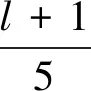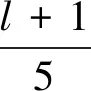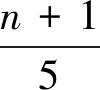两类乘积图的符号控制数

徐保根，张君霞，李 广

(华东交通大学 理学院，江西 南昌 330013)

0 引言

图的控制理论是图论中的重要内容，其研究内容越来越丰富，应用越来越广泛。本文中所指的图均为无向简单图,符号和术语同文献[1-2]。文献[3]综述了图的控制理论方面的主要研究成果，但绝大多数属于图的点控制[4-5]，很少涉及到图的边控制及全控制问题。近些年来，随着计算机技术的快速发展，图的标号理论得到了广泛应用，产生了图的控制函数概念[6]，从而引出了许多新的控制概念，如符号全控制[7-8]、符号圈控制[9]、F-控制[10-11]和符号边控制[12]等，极大地丰富和完善了图的控制理论内容，文献[2]已综述了近年来的研究成果。文献[13]首次提出并研究了图的符号控制概念，但确定这类控制参数是十分困难的，即使对于一些特殊的图类，确定其符号控制数的确切值仍然很困难，本文研究并确定了两类乘积图的符号控制数。

1 定义

设G=(V,E)是一个图，V(G)和E(G)分别为G的顶点集和边集。N(v)为v点的邻域，N[v]=N(v)∪{v}为v点的闭邻域，d(v)=|N(v)|为v点的度，△=△(G)和δ=δ(G)分别为图G的最大度和最小度。

定义1[1-2]设G1=(V1,E1)和G2=(V2,E2)为两个不交的图，则G1与G2的笛卡尔(Cartesian)积图(或称为乘积图)G1×G2定义为：

V(G1×G2)=V1×V2,E(G1×G2)={(u1,v1)(u2,v2)|u1=u2且v1～v2或者v1=v2且u1～u2}。

定义2[13]设G=(V,E)是一个图，一个双值函数f:V→{-1,+1}，如果对任意v∈V，均有f(N[v])≥1成立，则称f为图G的一个符号控制函数，图G的符号控制数定义为γs(G)=min {f(V)|f为图G的一个符号控制函数}。并称满足γs(G)=f(V)的符号控制函数f为图G的一个最小符号控制函数。

一般来说，确定一个图的符号控制数是困难的，对于乘积图Pn×Pm和Cn×Pm，当m=2时，文献[14]中给出了Pn×P2和Cn×P2的符号控制数：

而当m=3时，文献[15]中也给出了Pn×P3的符号控制数，但其结论与本文结论不一致。

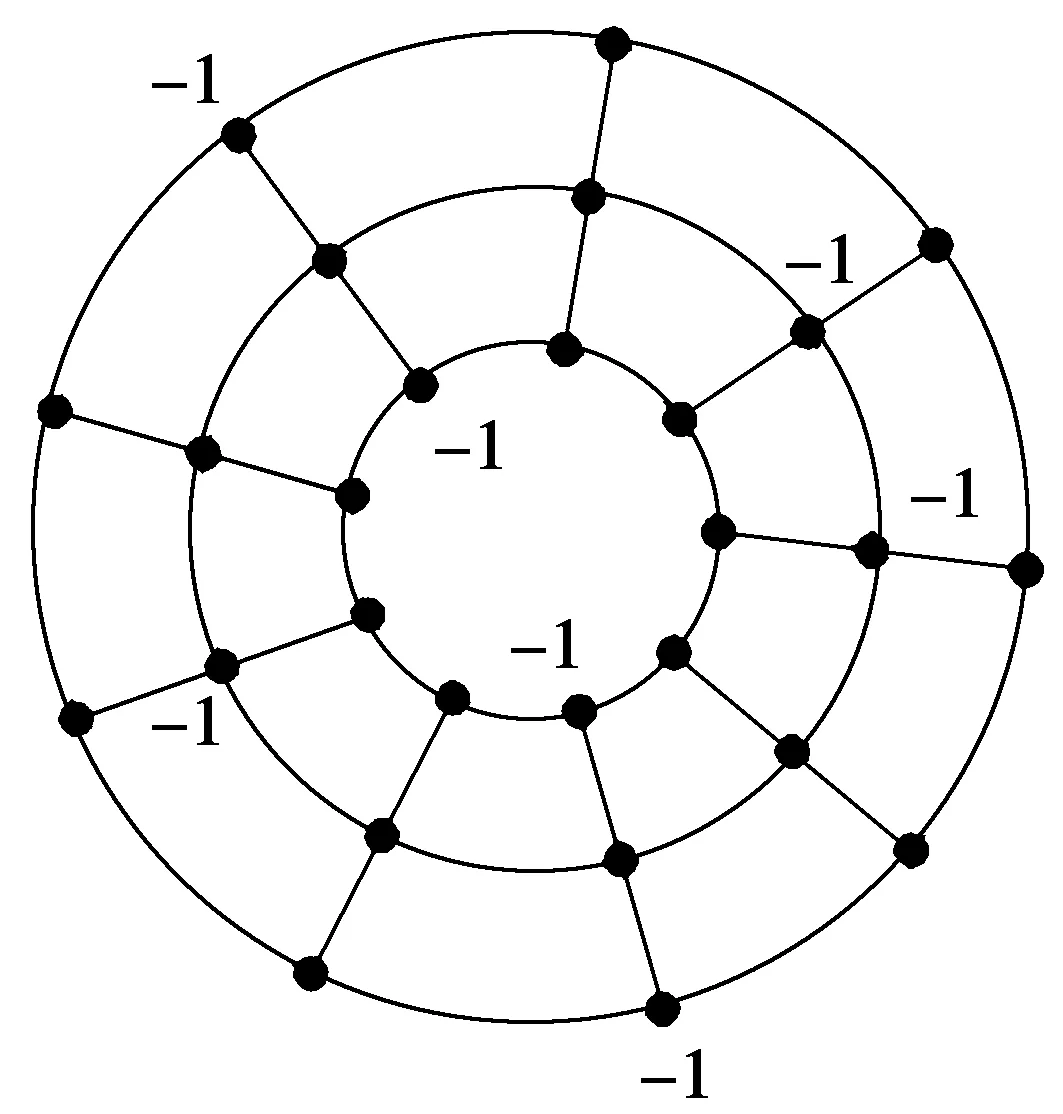
图1 C9×P3的符号控制函数

对于Cn×P3，本文获得了其符号控制函数，例如，当n=9时，C9×P3的符号控制函数见图1。不难验证，γs(C9×P3)≤13，其标号如图1所示(未标出的点均标号为+1)。

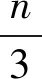
这一结论是不正确的。例如，当n=12时，按引理2则有γs(P12×P3)=20。

P12×P3的符号控制函数见图2。但图2显示γs(P12×P3)≤18，其标号如图2所示(未标出的点均标号为+1)。

本文将给出Pn×P3和Cn×P3的符号控制数的正确结果，首先用到引理3：

引理3γs(P5×P3)=7，并且对于图G=Pn×P3(n≥5)的任意一个符号控制函数f，在f下图G=Pn×P3的一端(3行5列)中标号为-1的点至多有4个。

引理3可以直接验证。事实上，P5×P3的一个最小符号控制函数(标号)f如图3所示(未标出的点均标号为+1)。

图2P12×P3的符号控制函数

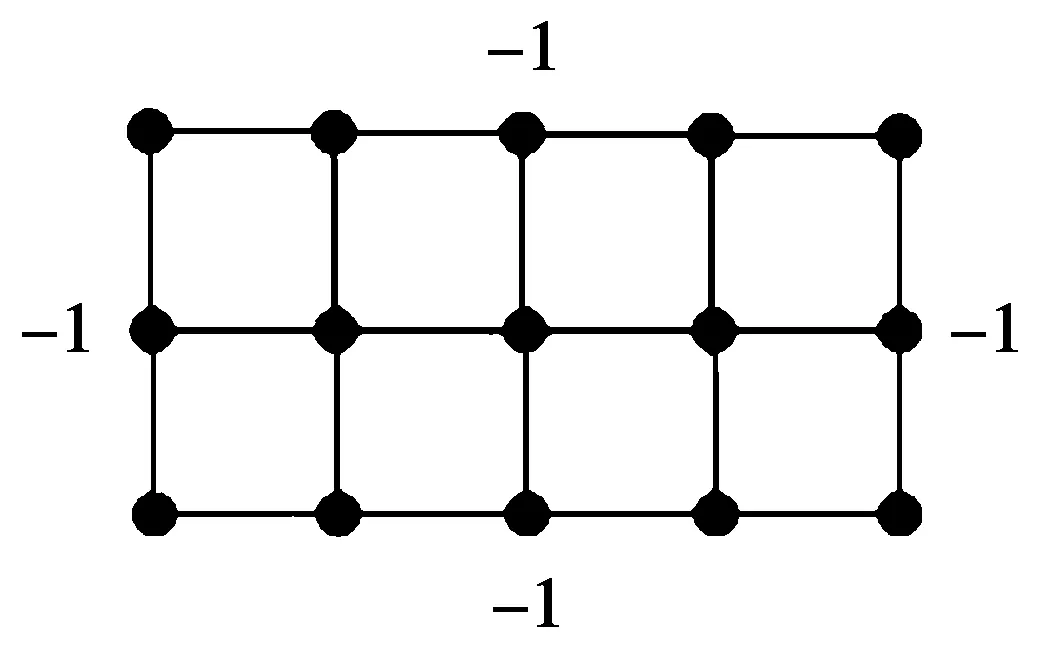
图3P5×P3的符号控制函数

2 主要结论及证明

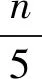
证明记G=Cn×P3，其顶点集V(G)=V1∪V2∪V3，在G中，令：

V1={u1,u2,…,un}，V2={v1,v2,…,vn}，V3={w1,w2,…,wn}；

E(G)={uivi,viwi|1≤i≤n}∪{uiui+1,vivi+1,wiwi+1|1≤i≤n}；

un+1=u1，vn+1=v1，wn+1=w1。

首先证明：

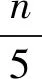
(1)

令f为图G的一个最小符号控制函数，即γs(G)=f(V)，记

A={v∈V(G)|f(v)=-1}，B={v∈V(G)|f(v)=+1}，

显然V(G)=A∪B，并且γs(G)=|B|-|A|=n-2|A|。只需证明式(2)即可：

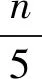
(2)

对于每个整数i=1,2,…,n，令Ai={uj,uj,wj|i+1≤j≤i+5}，这时下标取模n的最小正剩余。

另一方面，可以选取图Cn×P3的顶点集的一个子集A如下，并由其定义符号控制函数。

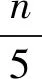
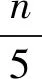
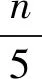
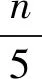
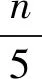
不难验证，f为图G=Cn×P3的一个符号控制函数，因此有：

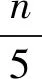
(3)

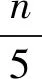
定理2设n≥3，则

(Ⅰ)γs(P3×P5)=7;

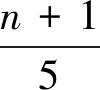
证明记G=P3×Pn，G为一个具有3行n列的格子图，第1、2、3行的点集标号见定理1。当n=5时，由引理3可知定理2成立，下设n≠5。

定义图G的一个函数g如下：

情况1若n=5k(k≠1)，令A={u2,w2,v4,v5,…,u5i+2,w5i+2,v5i+4,v5i+5,…,u5k-3,w5k-3,v5k-1}，则|A|=4k-1。

情况2若n=5k+1，令A={u2,w2,v4,v5,…,u5i+2,w5i+2,v5i+4,v5i+5,…,u5k-3,w5k-3,v5k-1,v5k}，则|A|=4k。

情况3若n=5k+2，令A={u2,w2,v4,v5,…,u5i+2,w5i+2,v5i+4,v5i+5,…,u5k-3,w5k-3,v5k-1,v5k,u5k+2}，则|A|=4k+1。

情况4若n=5k+3，令A={u2,w2,v4,v5,…,u5i+2,w5i+2,v5i+4,v5i+5,…,u5k-3,w5k-3,v5k-1,v5k,u5k+2,w5k+2}，则|A|=4k+2。

情况5若n=5k+4，令A={u2,w2,v4,v5,…,u5i+2,w5i+2,v5i+4,v5i+5,…,u5k-3,w5k-3,v5k-1,v5k,u5k+2,w5k+2,v5k+4}，则|A|=4k+3。

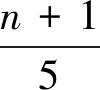
不难验证,g是符号控制函数，从而有

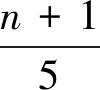
(4)

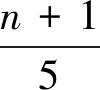
设f为G的一个最小符号控制函数，即f(V(G))=γs(G)。令M={u∈V(G)|f(u)=-1}，|M|=m，P={u∈V(G)|f(u)=1}，|P|=t，可见m+t=3n。

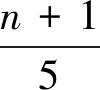
对n用归纳法：