轨道交通用永磁同步电机系统的延时补偿策略

景晓东

(中国中车永济电机有限公司，西安 710054)

0 引 言

与传统工业领域的永磁同步电机驱动系统不同，为了在低开关频率下获取较好的输出电流性能，轨道交通用永磁同步电机驱动领域通常采用多模式脉宽调制来优化谐波性能，其调制模式如图1所示，包括低速段的异步和同步SVPWM；中高速的特定次谐波消除脉宽调制(以下简称SHEPWM)及额定转速以上的方波调制。目前，在电驱动系统中，系统延时通常包括逆变器非线性延时和计算延时。对于前者，文献[1]指出，死区时间、IGBT导通和关断时间会在基波频率较低时对逆变器的输出电压性能产生较大影响；而在高转速区，相比于有效高电平信号的持续时间，逆变器非线性延时可以忽略。另一方面，当转速较高时，数字系统本身固有计算延时是不能忽略的，“差拍”现象会在此时产生较大的磁场定向误差。

图1 轨道交通电驱动系统多模式脉宽调制模式

关于逆变器非线性延时的研究已在永磁同步电机驱动系统的实际应用中开展多年。特别是在无机械位置传感器等电驱动领域，需要利用基波相电压才能获取最终的有效信号[2-3]。但由于相电压无法从逆变器输出端直接获取，通常采用指令值代替实际值。此时，受死区时间，功率器件导通、关断时间等逆变器非线性因素的影响，相电压指令值与实际值会存在较大偏差，从而使逆变器输出电压及电机端激励电流的谐波成分均显著增加。

为了解决上述问题，已有较多文献针对这一特性进行了补偿，通常包括两种思路：将逆变器非线性补偿电压(以下简称INCV)叠加到指令电压中[4-5]；将离线或在线获得的死区补偿时间(以下简称INCT)直接叠加到PWM高电平信号的持续时间中[6-7]。对于前者，在文献[8-10]中，一种补偿电压的自适应观测方法被用于消除逆变器非线性延时的影响，而状态观测器和前馈环节的引入使计算模型较为复杂。对于补偿时间的计算，文献[11-12]是在精确的逆变器非线性建模基础上完成补偿，同时，文献[11]是离线计算补偿时间。此外，也有文献通过增加检测电路，封锁与续流二极管反并联的IGBT门驱动信号[13]，达到无需设置死区时间的目的，但增加了硬件负担。综合以上分析可以看出，现有的逆变器非线性延时补偿方法均是在异步调制下完成的，对轨道交通多模式脉宽调制下的应用效果并未探讨。

当基波频率较高时，低载波比下的计算延时会使基波信号出现较严重的幅值衰减和相位滞后。针对这一问题，文献[14]将一种延时模型用于反电动势估计，改善了交直轴电流的耦合现象。文献[15]针对计算延时对永磁同步电机无位置传感器控制的影响展开研究，并通过一种改进的信号处理方式消除了由数字差拍引起的位置估计误差。而现有方法也并未结合多模式脉宽调制进行系统时延补偿策略的整体设计。

基于以上分析，针对轨道交通用永磁同步电机变频驱动系统，本文提出了一种改进的系统延时补偿策略。在低速SVPWM调制时，仅考虑逆变器非线性延时的影响，设计了一种自适应扰动观测器，利用q轴扰动电压获得逆变器非线性延时补偿时间；在中高速SHEPWM调制时，通过对电压矢量角和调制度的简单预测消除计算延时的影响。仿真和实验结果验证了此方法的有效性。

1 驱动系统中的延时作用原理

图2给出了永磁同步电机(以下简称PMSM)驱动系统在控制中使用的三相坐标系空间示意图，A，B，C轴为三相电流的磁场方向，d轴为永磁体磁场方向，且q轴超前其90°。同时，d，q坐标系随着转子同步旋转。在系统延时补偿策略的设计中，本文的逆变器非线性延时补偿策略也是基于q轴扰动电压完成的，且补偿器的详细设计将在后面给出。

图2 PMSM空间坐标系分布

当iA>0时，图3给出了逆变器A相输出电压理想值与实际值之间的关系。在逆变器非线性延时中，由于死区时间Tdead的存在，实际输出电压会变为

图3 逆变器非线性延时影响的A相输出电压特性

UAN_1。此外，受IGBT导通和关断时间Ton及Toff的影响，输出电压又变为UAN_2。最后，IGBT和并联二极管的导通压降UIGBT和UD被考虑后，输出电压变为UAN_3，则可得理想值和实际输出值的差：

(1)

iA<0的情况与图3类似，为了补偿逆变器非线性延时的影响，在PMSM矢量控制中，可将死区补偿电压叠加到由电流调节器输出的指令电压上。以A相为例，INCV与一个开关周期Ts内的电压平均值ΔUAN相关，且对应的A相死区补偿电压可表示：

(2)

式中：Tcom为逆变器非线性延时补偿时间(以下简称INCT)；Ts为开关周期；UDC为母线电压。这里，INCT可以被表示：

Tcom=Tdead+Ton-Toff+(Uon/UDC)Ts

(3)

式中：平均导通电压Uon可被定义：

(4)

值得注意的是，在式(14)中，电流为正或负值时的平均导通电压是几乎相同的。这是由于iA>0时的IGBT导通时间与iA<0时的关断时间大小相同，反之亦然。同理，亦可推导出B相和C相的INCV表达。

表1给出了本文使用逆变器的延时相关参数，为了与实际轨道交通电驱动特性相符，死区时间被设置为30 μs。图4给出了不同相电流有效值下由示波器显示的IGBT和二极管导通电压。在实测中，UD均大于UIGBT，由式(4)可知，当iA>0且相电流有效值恒定(负载恒定)时，平均导通电压Uon随着转速的减小而增大，这是由于IGBT导通时间Ton在低转速区要小于高转速区，即平均导通电压更依赖于二极管导通电压。另一方面，在图4中，UIGBT和UD均随着相电流的值变化，则平均导通电压也受负载大小的影响。此外，由于寄生电容的存在，IGBT的关断时间Toff在电机不同运行状态也是不同的。综合以上分析，表1中所列出的电压和时间值并不是一直准确的，即INCT在不同运行工况下是不同的，且独立测量不同条件下的IGBT特性参数具有较大难度。以此为出发点，本文探究了INCT的在线辨识方法。

表1 逆变器非线性延时相关参数

图4 实际逆变器的IGBT和二极管导通电压性能

图5给出了计算延时的作用机理。可以看出，在控制算法的执行过程中会存在一个采样周期的延迟。更新后的PWM信号会实际作用于t+Ts到t+2Ts之间。

图5 数字系统PWM更新时序

2 改进的系统延时补偿策略

2.1 逆变器非线性延时补偿中的INCV计算

式(2)给出了A相INCV的表达式，按照3/2变换可得到d,q坐标系下的补偿电压表达式，变换矩阵可表示如下：

(5)

q轴INCV是一个直流脉动电压信号，其最大脉动幅值可表示如下：

(6)

(7)

在后续文章中，INCTTcom的在线辨识也是基于q轴平均补偿电压。

表2 id=0时的d,q轴系INCV理论值

2.2 INCT辨识及q轴扰动电压估计

由式(6)可得INCT的解析计算方程如下：

(8)

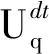
(9)

由表2可知，最大补偿电压幅值也是与d轴电压扰动相关的，但随着转速上升，由于d轴扰动电压的基波频率超过了扰动观测器的带宽，则实际扰动值并不能较好地与补偿值吻合。此外，id=0也决定了d轴INCV的平均值在理论上趋近于零。因此，估计的d轴电压并不适用于辨识INCT。相反，q轴扰动电压是一个直流信号且其平均值可用于估计INCT，在这种情况下式(9)几乎不受驱动频率增加的影响。基于以上原因，INCT的在线辨识仅使用估计的q轴扰动电压。

这里，d,q轴系下的电压方程可表示：

(10)

式中：R为电枢电阻；L为电枢电感；p为微分算子，Uddec和Uqdec可表示如下：

(11)

式中：ωr为转子电角速度；KE为反电动势常数。在闭环控制中，指令电压是由电流调节器输出的，其输出方程也会受到扰动电压的影响，如下:

(12)

当考虑逆变器非线性补偿电压后，式(12)可变为：

(13)

(14)

基于式(14)，扰动电压观测器可构建如下：

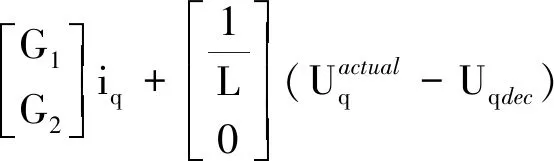
(15)

式中：G1=-(R/L+P1+P2)，G2=-LP1P2，P1和P2为观测器极点。图6给出了系统延时补偿原理框图。结合式(9)和式(15)可以看出，在获得q轴扰动电压的估计值后，需要将其等效为平均值，等效原理如图7所示。以半个基波电流周期为时间间隔，通过对过零点进行判断，即可求得对应时间段的平均补偿电压，随后代入式(9)可得INCT的估计值。结合INCT，由式(2)可求得A相补偿电压，同理求得B相与C相的补偿值，共同叠加到三相指令电压上，即可完成全部补偿过程。

2.3 SHEPWM调制时的计算延时消除

图8给出了SHEPWM的执行原理，M是调制度，N为1/4周期开关角个数，对应到7分频、5分频和3分频的SHEPWM，N值分别为3、2和1。β为d，q坐标系的电压矢量角。这里,调制度M的存储精度为0.01。由于转速被认为恒定，可通过下式对转子位置角和电压矢量角进行简单预测：

(16)

图8 SHEPWM的数字执行原理

3 实验结果分析

3.1 实验波形说明

本文采用双采样双更新的PWM计算时序，表3给出了仿真和实验过程中所用PMSM的主要电机参数。在图6中，转速和电流调节器均使用PI结构，控制参数的设计如表4所示。这里，极点P1和P2的选择对观测器性能有很大影响，以式(15)中q轴估计电流为分析对象，在基于载波的SVPWM调制下，图9给出了不同观测器极点下的q轴电流估计结果对比。图10给出了逆变器非线性延时补偿方法中涉及的估计性能体现，其中，电机给定转速被设置为200r/min，基波频率6.7Hz，加载0.21N·m(额定转矩的35%)，且d轴电流采用id=0控制。图11给出了电机转速200r/min时逆变器非线性延时补偿前后的A相电流性能对比。当使用7分频SHEPWM调制时，图12给出了计算延时消除前后A相电流性能对比。

表3 PMSM电机参数

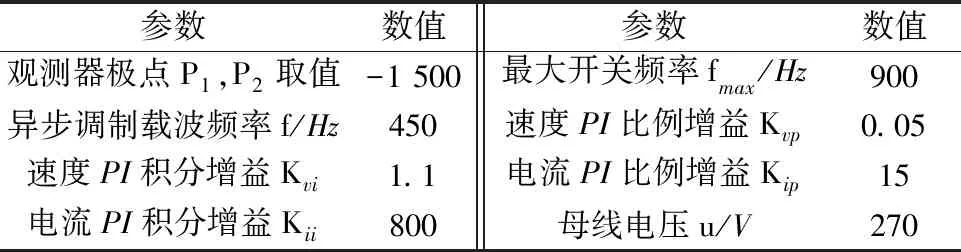
表4 控制参数

3.2 实验结果分析

由图9的观测器极点配置结果可以看出，当P1=P2=-500时，q轴估计电流存在较大波动，则对应的式(15)中的扰动电压估计值也会出现较大偏差。当观测器极点配置为-1 500时，q轴电流波动被完全消除，达到了较好的估计效果。当观测器极点位于-2 500时，高频电流成分也被估计出来，导致电流平滑程度略有下降。而对于实际应用，q轴电流采用了平均化策略，并不需要高频成分，则本文最终在实验部分选择了极点为-1 500来设计观测器。

图9 不同观测器极点配置下的q轴电流估计结果

在图10中，尽管估计的q轴扰动电压与理想的INCV有较好的吻合程度，但由于极值的存在，在某些时刻估计扰动电压的最大值高于理想的INCV，从而也会导致INCT辨识的不准确。为了克服这一问题，利用q轴扰动电压的平均值来进行补偿时间的辨识。由图7可以看出，q轴平均补偿电压的估计值与理想值没有明显区别；同时，A相补偿电压的计算值和理想值也基本一致。在图11中，死区补偿后A相电流的畸变程度被明显抑制，电流波动幅值的降低也进一步证明了补偿方法的有效性。由图12可以看出，当转速较高时，计算延时的消除使电流滞后明显消失，磁场定向精度的提高也使电流更加平滑。

图10 200 r/min时的INCV估计结果

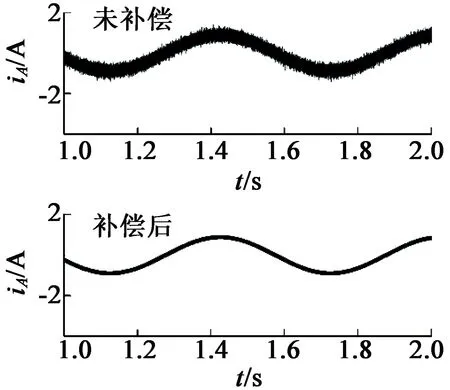
图11 200 r/min时逆变器非线性延时补偿前后的

图12 1 500 r/min时7分频SHEPWM调制A相电流对比

4 结 语

本文针对PMSM矢量控制系统，在id=0的条件下提出一种改进的系统延时补偿策略。首先，在低速段SVPWM调制时，考虑死区时间、开关器件导通/关断时间等逆变器非线性延时因素后，分析了INCT随不同工况的变化规律。随后，分析了d，q坐标系下INCV与INCT的对应关系。以此为基础建立q轴扰动电压观测器，利用平均值原理完成对INCT的在线辨识，并最终实现对三相给定电压的实时在线补偿。在中高速的SHEPWM调制区，通过对电压矢量角的简单预测，即可消除计算延时的影响。实验验证了改进的延时补偿策略在不同运行点的有效性。