一种旋转变压器电气精度的仿真分析方法
许兴斗,王永博,周竞捷,周奇慧
(中国电子科技集团公司第二十一研究所,上海 200233)
0 引 言
正余弦旋转变压器作为一种高精度角度传感器,其输出为与转子转角成正余弦关系的电压信号,常应用于武器装备系统中作为角度解算元件及随动系统位置传感器。正余弦旋转变压器具有可靠性高、精度高,维护简单、使用方便等特点,特别适合在恶劣工况和某些特殊场合中应用。
传统的旋转变压器设计方法为等效磁路法,根据主要技术指标和结构尺寸,通过迭代计算,完成旋转变压器原方及副方绕组匝数的设计[1]。等效磁路法无法考虑磁路中非线性及谐波磁场的影响,因此计算结果不太准确,误差较大。为克服等效磁路法的不足,可以采用有限元分析法,将电磁场的微分方程求解问题转化为泛函求极值问题。有限元分析法可以准确地计算出旋转变压器的磁场以及输出电压信号。因此,目前常采用有限元电磁仿真软件对正余旋旋转变压器进行电磁仿真。
用有限元电磁仿真软件对旋转变压器进行分析的局限性是无法直接得到电磁方案中的电气精度。目前,旋转变压器的仿真分析大多是通过输出电压信号的正弦性和正余弦输出信号的正交性来间接评价电磁设计方案的好坏[2]。
本文研究了一种旋转变压器电气精度的仿真分析方法,即应用有限元电磁软件Maxwell准确计算出旋转变压器输出信号,并使用MATLAB/Simulink软件对输出信号进行计算,计算出旋转变压器转子各位置下的电气误差,通过仿真可以直接得到旋转变压器设计方案的电气精度。
1 基本原理
旋转变压器由定子和转子组成,定、转子铁心中均分布有正弦绕组,R1,R3为激磁绕组,通入激磁信号URef;S1,S3为余弦绕组,输出余弦信号Ucos;S2,S4为正弦绕组,输出正弦信号Usin。电气原理图如图1所示。

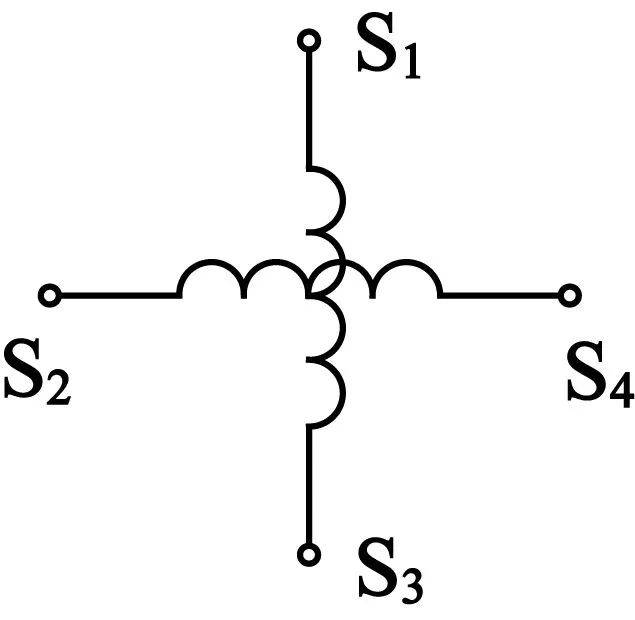
图1 电气原理图
旋转变压器电压方程式如下:
UR1R3=URef=Usin(ωt)
(1)
US1S3=Ucos=KUsin(ωt)cos(pθ)
(2)
US2S4=Usin=KUsin(ωt)sin(pθ)
(3)
式中:U为激磁电压的有效值;ω为激磁角频率;K为变压比;p为旋转变压器的极对数;θ为转子位置;pθ为转子电气角度位置。
由电压方程可知,旋转变压器转子在角度位置θ处,其输出信号为以ω为周期,KUsin(pθ′)、KU·cos(pθ′)为幅值的正、余弦输出信号。计算的实际位置θ′与位置θ的差值,即为旋转变压器在该位置的电气误差δθ[3],也称之为电气精度。
按照GJB2143A多极和双通道旋转变压器通用规范中电气误差的测试方法规定,应测试所有零位的零位误差。在最大正、负零位误差所处零位的极对下各测一对极的电气误差,每对极测24点(电气角度每隔15°测一点),取各位置误差中的最大值的绝对值|δmax|为旋转变压器的电气误差。
2 电气精度仿真计算方法
根据“反正切法”可以计算出旋转变压器的角度位置。通过有限元仿真得到旋转变压器在pθ电气角度位置处的两相输出电压波形,计算得到两相输出电压的有效值|Ucos|和|Usin|,反正切计算出角度位置:
pθ1=arctan(|Usin|/|Ucos|)
(4)
结合两相输出电压Ucos,Usin和激磁电压UR1R3进行象限区间判定,可以得到旋转变压器的实际角度位置:
pθ′=pθ1+i×90°(i=0或1或2或3)
(5)
那么旋转变压器在pθ位置处的电气误差:
δθ= (pθ′-pθ)/p=θ′-θ
(6)
电气精度计算方法如图2所示。

图2 计算方法
3 电气精度的仿真分析
旋转变压器的电气精度仿真包含两个步骤,首先应用有限元电磁仿真的方法得到旋转变压器在不同位置下输出电压信号的波形和数据,然后再应用计算方法得到旋转变压器的电气精度。
3.1 有限元电磁仿真
一款多极旋转变压器的设计参数如表1所示。采用美国Ansoft公司的Maxwell有限元仿真软件对该多极旋转变压器进行仿真。
根据表1中的主要参数,采用Maxwell软件中Maxwell 2D建模,模型如图3所示。
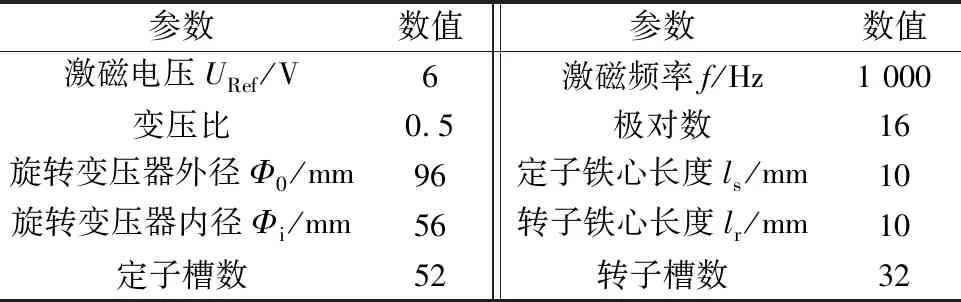
表1 样机主要参数

图3 多极旋转变压器模型
完成仿真模型中的绕组分相、匝数设计、激磁设置、剖分设置、计算方法设置,对旋转变压器进行电磁仿真。
多极旋转变压器的磁力线图如图4所示,从图4中可以看出,磁力线走势正确,说明所建的模型准确。

图4 磁力线图
多极旋转变压器的磁密云图如图5所示,由于旋转变压器的激磁电压不高,磁密云图中的气隙主磁场、齿部和轭部等均未出现磁密饱和的情况,各个位置的磁密值设计合理。

图5 磁密云图
旋转变压器转子转动时,仿真得到多极旋转变压器的激磁信号及输出信号。激磁信号波形如图6所示,正弦输出信号及余弦输出信号波形如图7所示。

图6 激磁信号波形

图7 输出正余弦信号波形
从图7中可以看出, 正、余弦输出信号的包络线正弦性良好,两相信号正交,说明仿真方法正确。
按照多极和双通道旋转变压器通用规范中电气精度的测量方法,在一个电周期内每隔15°电角度测一点,因此在电磁仿真中需要得到转子每隔15°电角度位置下的正、余弦输出信号。
旋转变压器为16对极,一个电周期内转子各位置机械角度间隔为15°/16=0.937 5°,共计24个位置。分别仿真得到旋转变压器在24个位置下的正弦输出信号和余弦输出信号。24个位置下的正弦输出信号如图8所示,余弦输出信号如图9所示。

图8 各位置下的

图9 各位置下的
3.2 电气精度计算
应用MATLAB/Simulink软件,依据图2的精度计算方法搭建模型,如图10所示。

图10 计算模型框图
将电磁仿真得到的各个位置下多极旋转变压器的正、余弦输出电压数据和激磁电压数据导入计算模型中,可以计算出在24个不同位置点下的转子实际位置,如图11所示。

图11 计算转子位置
图11计算出的各转子位置与图8、图9中的位置一一对应,旋转变压器为16对极,一个电周期对应的机械角度为360°/16=22.5°,图11计算出的各个转子位置角度几乎在一条直线上,说明样机的电磁方案合理。一个电周期内旋转变压器的电气精度曲线如图12所示,在一个电周期内电气误差的最大值为14″,电气误差的最小值为-20″。

图12 转子不同位置下的电气误差曲线
4 仿真结果与实验对比
按照表1中给出的主要参数,设计制造的多极旋转变压器样机实物如图13所示,其电磁设计方案与电磁仿真模型完全相同。

图13 多极旋转变压器样机
将2台样机按照一个电周期内每隔15°电角度测一点进行电气误差的测试,2台样机的实测电气误差曲线(取电气误差最大值所处的一个电周期)分别如图14、15所示。

图14 1号样机电气误差曲线

图15 2号样机电气误差曲线
1号样机在一个电周期内电气误差的最大值为22.3″,电气误差的最小值为-18.8″;2号样机在一个电周期内电气误差的最大值为20.5″,电气误差的最小值为-6.2″。
将仿真结果与两台样机产品的实测结果进行对比可以看出,两者曲线的变化规律和电气误差绝对值的极大值在量级上都是接近的。因此,通过这种有限元仿真加计算的分析方法可以模拟旋转变压器的电气精度,对电磁设计方案的合理性作出判断,从而指导旋转变压器产品的设计。
从图12的仿真曲线明显可以看出,要比图14和图15样机的实测曲线要对称,主要原因是仿真中不用考虑产品实际设计、加工及测试中带来的偏差,如磁性材料各向导磁率是否一致、定转子之间气隙是否完全均匀、铁心齿槽分度带来的误差以及安装测试中引入的误差等。从图12及图14、图15中还可以看出,误差曲线呈高次谐波的形式,这主要是旋转变压器本身所固有的,例如:正弦绕组的结构设计方法不完善,斜槽不准确,定、转子的槽数选择不合理等,致使某些高次空间谐波磁场感应的电压没能充分抑制掉;另外,铁心的气隙磁密分布的波形非正弦,加工中的偏心、椭圆以及安装时定、转子轴不同心等都会引起误差。随着设计、工艺、测试等手段的不断完善,磁性材料的不断更新,这类误差是可以消除或减小的。
5 结 语
本文阐述了一种针对旋转变压器电气精度的有限元仿真加计算的分析方法,通过对一款旋转变压器进行仿真分析并与样机实物测试的结果对比,验证了该电气精度仿真分析方法的可行性,对提高旋转变压器精度设计的精准性具有较高的实用工程价值。

