非幂零极大子群个数的2个下界
卢家宽,陈婵婵,王申洋
(广西师范大学 数学与统计学院,广西 桂林 541006)
本文涉及的群均为有限群,文中使用标准的术语及符号,可参考文献[1].G表示有限群,|G|表示的阶,π(G)表示整除|G|的素数构成的集合,m(G)表示G的极大子群的个数.在有限群理论的研究中,关于极大子群数量的研究有丰富的成果.例如,Newton[2]证明了当G是可解群时,有
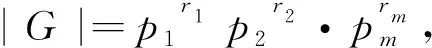
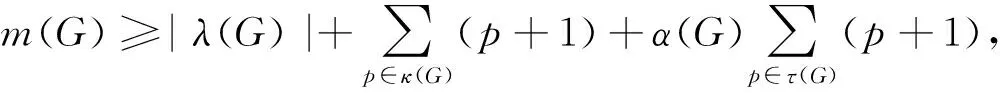
其中τ(G)⊆π(G)表示满足G非p-可解的素因子p的集合,λ(G)⊆π(G)表示满足G是q-可解且Sylowq-子群循环的素因子q的集合,κ(G)⊆π(G)表示满足G是q-可解且Sylowq-子群非循环的素因子q的集合,α(G)为常数.卢家宽和孟伟[4]证明了如果最多有2个非幂零极大子群共轭类,那么G是可解群.
我们使用n(G)表示G的非幂零极大子群的个数.本文主要给出n(G)的2个下界.
1 引理
这里列出本文使用到的几个主要引理.
引理1[1]设G是有限群,若N是G的可解极小正规子群,则N是初等交换p-群,p∈π(G).
引理2[5]设G是有限群,则有m(G)≥|π(G)|.此外,上述不等式等号成立当且仅当G为循环群.
引理3设G是有限非可解群,m和n分别是π(G)中最大的素数和最小的素数,则有m≥|π(G)|+n.
证明:显然,除了2和3之间,任意两个连续的素数之间相差两个数.因此m-n≥2(|π(G)|-2)+1.又由Burnsidepaqb-定理可知|π(G)|≥3.于是,m-n≥|π(G)|即m≥|π(G)|+n,引理得证.
2 主要结果
定理1设N是有限群G的非交换极小正规子群,p是π(N)中最大的素数.令N=R1×R2×…×Rl是同构单群的直积,则至少有pl个不包含N的非幂零极大子群.
证明:令P是N的Sylowp-子群.由Frattini论断,有G=NNG(P).又Z(J(P)) charJ(P),J(P) charP,于是Z(J(P)) charP.又P◁NG(P),于是Z(J(P))≤NG(P),故NG(P)⊆NG(Z(J(P))).显然,NG(Z(J(P)))≠G.若否,则有Z(J(P))◁G是包含在N内的G的正规子群,与N的极小正规性矛盾.
令M是G中包含NG(Z(J(P)))的极大子群.则
G=NNG(P)=NNG(Z(J(P)))=NM.
如果M是幂零的,则NG(Z(J(P)))是幂零的,从而NN(Z(J(P)))是幂零的.若p=2,则N是2-群,由引理1知N是交换群,与假设矛盾.若p>2,由Glauberman-Tompson正规p-补定理知,N是p-幂零的,与N的极小正规性矛盾.于是M是G的不包含N的非幂零极大子群.
令Si=Ri∩M,i=1,2,…,l.由于M在{R1,R2,…,Rl}上传递作用,因此Si和Sj是M-共轭的,i,j=1,2,…,l.又N是同构单群的直积,故而Ri⊄M.同时,Ri≠Si≠1且Si在Ri非正规.于是M在G中非正规,且M是G的自正规化极大子群.
令Ri左乘作用在所有Si在Ri中的左配集构成的集合上.因此Ri同构于交错群A|Ri∶Si|的一个子群.于是p≤|Ri∶Si|.不妨设Ti是M∩N到Ri投影映射的像.由于Ri◁N,因此Si◁M∩N,故而Si◁Ti.又Ri是单群,所以Ti是Ri的真子群.于是U=T1×T2×…×Tl是N的真子群.因此M正规化U且UM是G的真子群.又M的极大性,所以U⊆M且Ti⊆Si.显然Si⊆Ti,因此Si=Ti.于是
|G∶M|=|N∶N∩M|=|R1×R2×…×Rl∶S1×S2×…×Sl|≥pl.
综上所述,G中至少有pl个不包含N的非幂零极大子群.
定理2设G是有限非可解群,则有n(G)≥|π(G)|+p,其中p=min{q∈π(G)|G的Sylowq-子群在G中正规}.
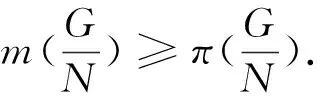
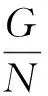
定理2对可解群不一定成立.例如,幂零群,内幂零群.我们有例2.1:
令p>1是素数,m|p-1且|π(m)|≥2,则存在阶为pm的非幂零且非内幂零的有限可解群G,使得n(G)≤|π(G)|-1.



