基于短时傅立叶变换特征提取和卷积神经网络的LAMOST恒星光谱分类研究

杜利婷, 自彦丞, 张静敏, 艾霖嫔,周卫红, 2

(1.云南民族大学 数学与计算机科学学院, 云南 昆明 650500;2.中国科学院 天体结构与演化重点实验室, 云南 昆明 650011)

研究恒星光谱的重要内容之一是恒星光谱分类, 准确识别分类恒星光谱对天文研究有重大意义. 目前通用恒星光谱分类方法是摩根-基南(Morgan-Keenan, MK)分类法, 即MK系统分类方法, 其依据恒星温度由高至低排序, 将恒星光谱分为O, B, A, F, G, K 和 M 型7大类, 其中, O型有5小类, M型有6小类, B, A, F, G, K型分别有10小类, 总共有61小类. 目前, 国内大型巡天项目LAMOST (large sky area multi-object fiber spectroscopic telescope)每年产生数百万恒星光谱数据, 对大量恒星光谱进行准确识别与分类研究已经成为天文研究热点之一.

2017年12月31日, LAMOST项目一期低分辨率(R= 1 800)巡天工作正式宣布结束, LAMOST DR5数据集正式发布, 共发布了901万条光谱, 其中高质量光谱数(S/N > 10)达到了777万条. 2017年9月1日起, LAMOST开始第2期中分辨率(R= 7 500)巡天, 2019年3月27日, LAMOST DR6数据集正式发布, 共包含 1 125 万条光谱, 包括常规低分辨率光谱数据和中分辨率测试光谱数据, 其中, 低分辨率光谱数据总数991万条, 中分辨率非时域光谱数据50万条, 中分辨率时域光谱数据84万条; 这其中高质量光谱(S/N > 10)达到了937万条, 约是国际上其他巡天项目发布光谱数和的2倍, LAMOST成为第1个超过千万量级的巡天项目, LAMOST获取的天文大数据丰富了全球天文观测数据库;

在恒星光谱分类研究方面, 刘蓉等[1]提出了1种结合非参数回归与自适应增强算法(adaptive boosting, adaboost)对恒星光谱进行MK分类的方法, 采用非参数回归方法进行恒星光谱型和光谱次型的分类, 基于adaboost方法组合一组K近邻分类器进行光度型分类,实验结果为光谱次型识别的精度达到0.22, 光度型分类准确率达到84%以上, 表明该方法的有效性; 王晶等[2]基于集成树模型对M型光谱进行分类研究, 实验结果表明集成树算法在巨星识别过程中具有显著优势; 潘景昌等[3]研究了基于Lick线指数的贝叶斯光谱分类方法, 对F, G,K3类恒星光谱进行分类; Liu等[4]提出基于恒星轨迹线指数对LAMOST中的A与G型恒星光谱数据进行自动分类, 分类准确率在90%以上;Liu等[5]分别运用局部保持投影法(locality preserving projections,LPP)和主成分分析(principal component analysis,PCA)对SDSS的F型与G型恒星光谱进行降维, 然后再利用支持向量机(support vector machine, SVM)对降维后的恒星光谱数据进行分类, 结果表明LPP的性能优于PCA.

随着LAMOST巡天数据的快速增长, 如何高效准确的处理海量光谱数据显得尤为重要, 而高效智能的方法随之产生. 2006年, Hinton等人提出深度学习. 深度学习源于神经网络, 其重要组成部分是机器学习; 近年来, 深度学习广泛运用于光谱分类研究方面, 并取得了一定的成果. S.Kherirdastan等[6]将概率神经网络(probabilistic neural network,PNN)、SVM和K-means算法作为大质量恒星光谱自动分类工具, 结果表明PNN的自动分类效果优于SVM和K-means算法; Mahdi等[7]将自组织映射网络(self-organizing mapping, SOM)算法作为1种无监督的人工神经网络算法用于恒星光谱的分类, 分类准确率约为92.4%; 许婷婷等[8]将深度信念网络应用于恒星光谱分类, 分类准确率达到93%; 石超君等[9]提出1种基于卷积神经网络的K和F型恒星光谱分类方法, 结果为99.8%, 结果比SVM和误差反向传播(error back propagation, BP)算法的准确率要高, 成功的将一维卷积神经网络运用于恒星光谱分类中; 刘忠宝等[10]在双支持向量机的基础上, 提出融合数据分布特征的模糊双支持向量机, 在SDSS DR8恒星光谱数据上进行研究, 结果表明相对于传统的支持向量机和双支持向量机, 融合数据分布特征的模糊双支持向量机具有更优的分类能力.

1 利用短时傅里叶变换和一维卷积网络生成新的特征谱图像

1.1 短时傅里叶变换

傅里叶变换(Fourier transformation, FT)由傅里叶在1807年为了解决热过程中的问题而提出,其最成功之处是将难以处理的时域信号转换成易于分析的频域信号, 然后再利用一些工具对频域信号进行处理和加工, 从而表示出时域信号的的特征. 但是, 对于一些不平稳信号, 比如说语音信号等, 其频域信号是随时间变化的, 而有时人们需要去了解某个时段上的频率特征, 对于这种时频局部化的要求, 傅里叶变换无法解决, 因而Dennis Gabor于1946年引入短时傅里叶变换(short time Fourier transform, STFT), 其基本思想是: 通过窗函数将信号切分成许多相同的小的时间隔, 用傅里叶变换分析每1个时间隔, 以此来确定该时间间隔存在的频率, 得到一系列频域信号的变化结果, 将这些结果排开便得到1个二维的表象, 进而再用相关工具去分析, 得到某个时段上的频率特征, 实现时频局部化. STFT的公式如下:

其中,f(t)是信号函数,g(t-τ)是窗函数,ω是信号函数中的基频率.

实验利用Specgram函数来实现短时傅里叶变换, 将一维恒星光谱数据转换成二维傅里叶谱图像, 形成新的特征分布且保留了更多特征, 有利于后续的分类研究. Specgram函数的语法如下:

[S,F,T,P]=spectrogram(A,window,noverlap,nfft,fs).

其中,A是信号;window是窗函数;noverlap是各段之间重叠采样的点数(各段之间必须要有重叠的部分);nfft是计算离散傅里叶变换的点数;fs是采样频率;S是输入信号A的短时傅里叶变换;F是在输入变量中使用F频率变量;T是频谱图计算的时刻点;P是能量谱密度. 在本文中,A被分成8段分别做变换处理;window是长度为nfft的海明窗;noverlap是在各段之间产生50%的重叠;nfft是256和大于每段长度的最小2次幂之间的最大值;fs为5.

1.2 一维卷积

由于在短时傅里叶变换中的采样过程会损失部分特征信息, 所以我们在短时傅里叶变换之前先对恒星光谱数据进行一维卷积处理, 目的是减少后续处理中的特征损失. 卷积神经网络的一般结构如图1, 图中包括输入层, 卷积层, 池化层, 全连接层, 输出层. 通常情况下, 数据集进入输入层进行预处理, 然后通过卷积层的卷积核提取特征进而生成特征图, 池化层对特征图进行特征选择和信息过滤以形成新的特征图, 全连接层对池化层生成的特征图进行整合, 最后输出结果. 而一维卷积的结构包括输入层, 卷积层, 输出层, 在没有池化层之后, 光谱数据经过一维卷积处理后仍然保持原来的维度, 继而对应的特征也保留.

对于一维卷积的结构, 首先在输入层输入F5, G5, K5型恒星光谱数据各1000条; 而在卷积层处, 我们设置了数量即深度为1, 尺寸为3× 1, 权值为1, 1, 1, 步长为1的卷积核; 在输出层输出经过卷积层处理后的结果. 举例说明一维卷积的具体计算过程, 其中, 卷积核的数量为1, 尺寸为3× 1, 权值为1, 1, 0, 步长为1, 并在输入光谱的两侧加上一圈宽度为1, 值为0的像素点, 即进行填充, 目的是保持光谱数据经过一维卷积处理后的维度不变, 如图2所示:

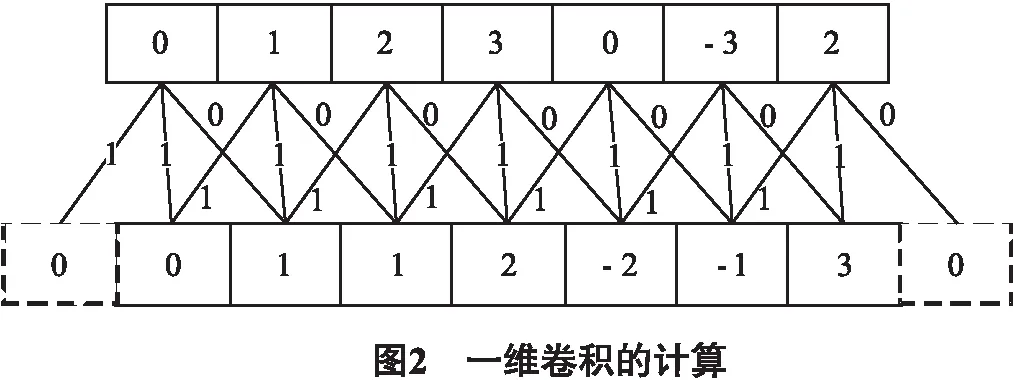
2 实验设计

2.1 恒星光谱数据的预处理

文中实验数据来源于LAMOST Data Release 5(DR5), 从中随机选取各1 000条共3 000条F5, G5, K5型恒星光谱数据, 信噪比>20, 每条光谱数据的波长范围是370～910 nm. 由于光谱数据在不同波长下对应的流量值可能存在很大的差异,不利于分类实验, 所以对数据进行归一化处理, 使流量值处于[0-1]之间, 以解决流量值变化区间处于不同数量级的问题, 文章采用的归一化方法如下:

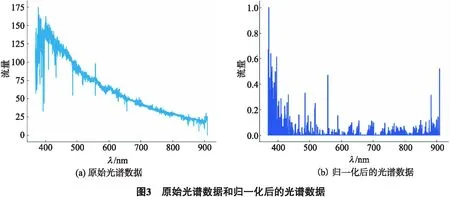
其中,χnorm表示归一化后的恒星光谱数据;χ=(χ1，…，χn)表示每一条光谱数据, 其中,χ1，…,χn表示给定波长下对应的流量值;Xmax=(χ1,…,χn)max,, 即一条光谱数据中最大的流量值, 经过归一化处理后, 恒星光谱数据中的流量值均映射到[0, 1], 处于用一个数量级, 有利于后续的分类实验. 一条未经过任何处理的和经过归一化后的F5型恒星光谱数据分别如图3中(a)、(b)所示.

2.2 一维卷积运算：

首先将3 000条恒星光谱数据进行一维卷积处理, 使恒星光谱原有的特征明显化和减少在短时傅里叶变换中采样过程的数据损失, 其中卷积核的数量为1, 尺寸为3× 1, 权值为1,1,1, 步长为1, 并在输入光谱的两侧加上一圈宽度为1, 值为0的像素点, 即进行填充, 以保持经过一维卷积后恒星光谱数据的维度不变.

2.3 短时傅里叶变换:

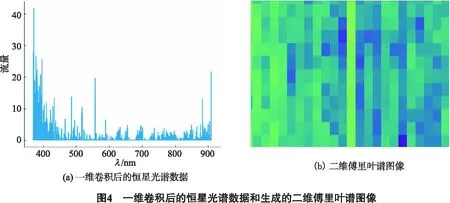
在经过一维卷积计算后的恒星光谱数据仍然为一维恒星光谱数据, 无法作为卷积神经网络的输入, 因此, 要利用STFT的时频解析性质将一维恒星光谱数据转化为二维傅里叶谱图像, 形成新的特征分布, 以有利于后续的分类研究. 一条经过一维卷积的F5型恒星光谱数据, 以及该条恒星光谱数据生成的二维傅里叶谱图像如图4(a)、(b)所示.

2.4 利用卷积网络对谱图像进行分类

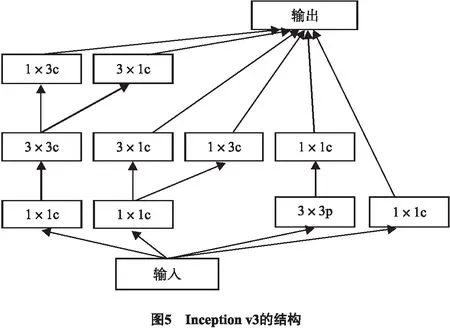
为了进行结果的比对, 设置了另外一组实验, 直接利用短时傅里叶变换将 3 000 条恒星光谱数据转换为二维傅里叶谱图像, 然后再利用Inception v3模型对二维傅里叶谱图像进行分类识别. 在这两组实验中, 短时傅里叶变换中的采样率fs均为5, 而Inception v3模型是深度学习中经典且有效的卷积神经网络. 它从Inception v1逐步发展而来, 相对于Inception v1和Inception v2, 在Inception v3模型中, 卷积核和池化堆叠在一起, 增加了网络的宽度和对尺度的适应性; 加入批次规范化(batch normalization, BN)层, 有助于加速收敛和提高准确率; 将一个较大的二维卷积核分成两个较小的一维卷积核, 减少参数, 加速运算并减轻了过拟合, 增加了1层非线性扩展了模型表达能力, 这种非对称的卷积结构拆分, 可以处理更多更丰富的空间特征, 增加特征多样性, 因而Inception v3的结构如图5所示(图中c是convolutions; p是max pooling).

3 结果分析

3.1 实验结果

文中提出在利用STFT之前, 先将来自LAMOST DR5的各1 000条F5, G5, K5型恒星光谱数据做一维卷积, 以减少在短时傅里叶变换的采样过程中造成的特征损失, 然后再利用STFT将恒星光谱数据转化为二维傅里叶谱图像, 最后利用Inception v3模型对二维傅里叶谱图像进行分类, 结果如表1所示:

表1 实验结果

由表1可知, 在第1组实验中, 恒星光谱数据没有做一维卷积, Inception v3模型的分类准确率为90.4%; 而在第2组实验中, 恒星光谱数据做了一维卷积, Inception v3模型的分类准确率为99%, 二者的差距十分明显, 从而表明一维卷积对于降低数据损失的有效性, 进而提高分类准确率.

3.2 实验分析

在文献[11]中, 张静敏等选取了LAMOST DR5中的F型, G型, K型恒星光谱数据各10 000条作为训练集, 各1 000条作为测试集, 然后采用深度信念网络(deep belief net, DBN)模型进行训练分类, 结果为94%; 在文献[12]中, 张静敏通过短时傅里叶变换生成新的特征谱图像, 再利用Inception v3模型对二维傅里叶谱图像进行分类实验, 实验数据来源于LAMOST DR5中的F型, G型, K型各10 000条, 最终的分类准确率为92.9%. 文献[11]与文献[12]中的实验结果与文中实验结果对比见表2.

表2 结果对比

由表2可知, 虽然本实验与文献[11]和文献[12]实验样本数据不同但都源于LAMOST DR5, DBN与Inception v3都属于深度学习中的模型. Inception v3是卷积神经网络的经典模型, 能有效提取图像的特征, 所以通过Inception v3模型对二维傅里叶谱图像提取特征然后进行分类. 从实验结果来看, 本实验的分类准确率达到99%, 是比较好的结果, 进而说明一维卷积对于降低数据损失的有效性, 进而提高分类准确率.

4 结语

为降低恒星光谱数据在短时傅里叶变换的采样过程中造成的数据损失, 文中采用短时傅里叶变换和一维卷积网络形成新的特征谱图像, 该特征谱图像形成新的特征分布且保留更多的数据信息, 进而提高分类准确率, 实验结果表明了一维卷积对于保留特征的有效性, 且分类效果优于其他分类模型. 深度学习方法面对大样本数据有较大优势, 但也有计算量大的缺点, 所以需要进一步优化算法以解决复杂度高的问题. 在接下来的工作中, 我们将会选取分类精度低的光谱作为分类候选体, 进行自动分类和数据挖掘研究, 相关成果可以为研究银河系结构提供进一步支持.