基于双光纤光栅的柔性铰链加速度传感器设计
梁 磊,朱振华,李美格,徐 刚,2
(1.武汉理工大学,光纤传感技术国家工程实验室,湖北武汉 430070;2.湖北工程学院机械工程学院,湖北孝感 432000)
0 引言
振动的现象是普遍存在的,大多数情况下,它会影响工程结构、机械设备、电子仪器的使用性能,严重时会导致灾难性事故[1-2]。因而,对于振动信号的测量显得极其重要。近年来,光纤光栅(FBG)加速度传感器在振动测试的领域内得到了充足的发展。相较于电类传感器,光纤光栅加速度传感器具有体积小、耐高温、抗电磁干扰、精度高和稳定性好等诸多优点[3-4]。因此,FBG加速度传感器被广泛应用于实际的工程领域中。目前,相关学者已经研究了多种结构形式的光纤光栅加速度传感器,常见的有梁式、膜片式和铰链式[5-9]。文献[10]提出了一种增敏型光纤光栅加速度传感器,该传感器的灵敏度较高,但其固有频率仅为70 Hz,工作的频率范围较窄。文献[11]设计了一种新型双光栅高频加速度传感器,该传感器的固有频率高达3 kHz,可实现高频测量,但忽略了分析传感器抗横向干扰的能力。
本文从柔性铰链的角度出发,在兼顾了其优点的同时,提出了一种基于双光纤光栅的柔性铰链加速度传感器。该传感器采用双光纤光栅对称推挽设计,双光栅对称结构不仅能够使灵敏度倍增,还具有温度自补偿的能力。理论分析了传感器的灵敏度和固有频率以及温度自补偿效应,并对传感器结构进行有限元仿真分析,根据分析的结果制作了传感器,并通过实验研究了传感器的性能。
1 传感器原理介绍与分析
1.1 传感器结构设计
加速度传感器结构如图1所示,其主要由基座、柔性铰链、质量块、L型梁和2个FBG组成。其芯体采用一体化加工的方式,柔性铰链在基座和质量块之间,2个FBG通过胶结剂两点粘贴于质量块和L型梁之间。当外界振动信号作用于传感器时,质量块受到惯性力的作用绕铰链中心相对基座转动,带动2个FBG分别拉伸和压缩,从而使2个FBG的中心波长产生漂移。

图1 传感器结构简图
1.2 传感器理论分析
图2为传感器的力学模型,当加速度a作用于传感器的质量块时,系统的力矩平衡方程为
mad-kΔl(R+b)-Kθ=0
(1)
式中:m为质量块的质量,kg;d为质量块质心到铰链中心的距离,m;θ为质量块转动的角度,rad;K为铰链的转动刚度,N/m;Δl为光纤拉伸的长度,m;k为光纤的弹性系数,N/m;R为铰链半径,m;b为质量块的长,m。
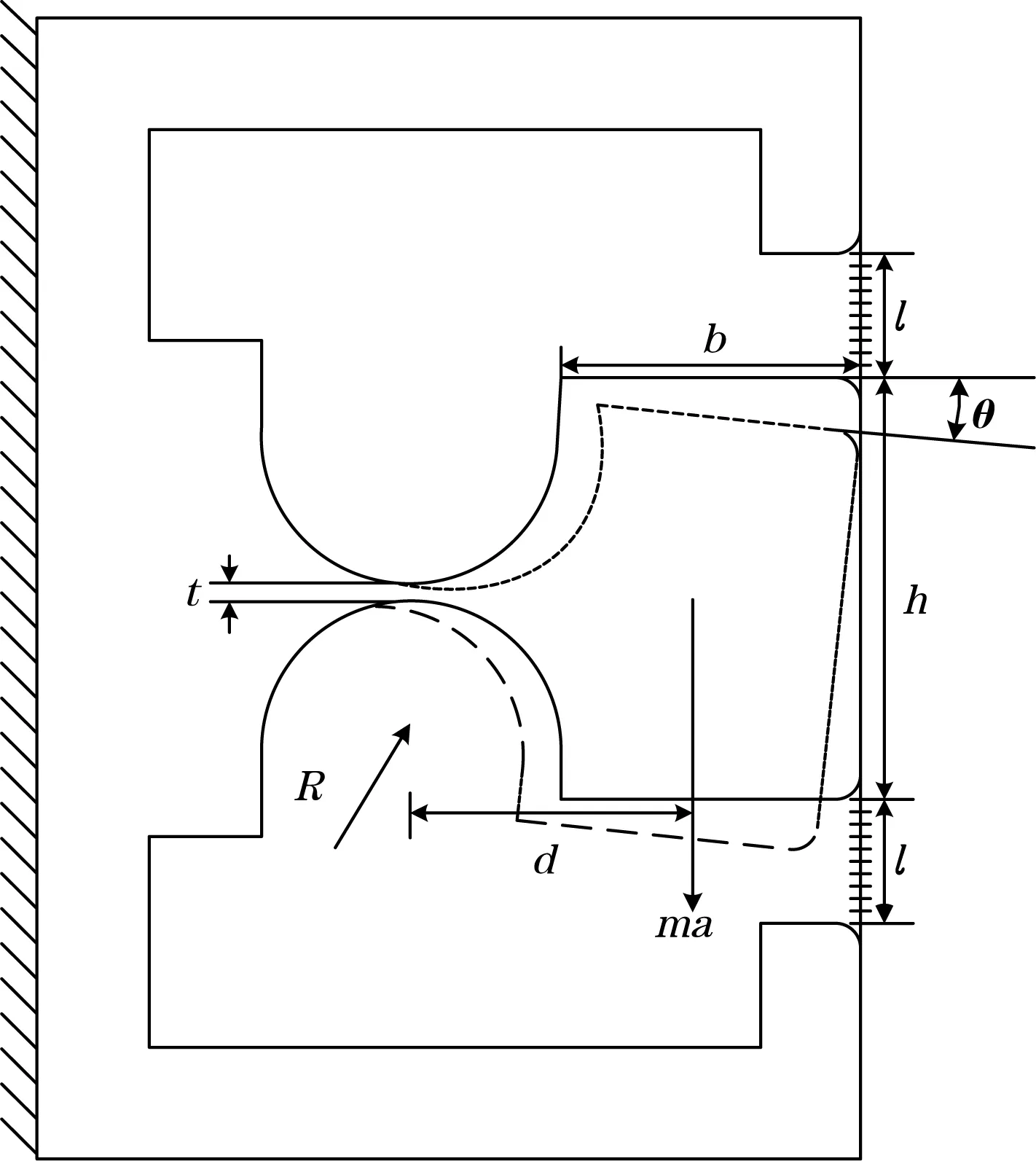
图2 传感器力学模型图
光纤的弹性系数为
(2)
式中:Ef为光纤的弹性模量为,Pa;Af为横截面积,m2;l为光纤光栅的栅区长度,m。
质量块转动角度为θ时,这时光纤光栅所产生的应变ε为
(3)
质量块的质心d为
(4)
铰链的转动刚度[12]K为
(5)
式中:E为铰链的弹性模量,Pa;i为传感器整体的厚度,m;t为铰链的最小厚度,m;s=R/t。
光纤光栅受到轴向拉伸或压缩时将产生应变,当不考虑温度对光纤光栅的作用,光纤光栅只受到轴向应变ε时,可以得到:
Δλ=(1-Pe)λε
(6)
式中:λ为光栅的初始波长,nm;Pe为光纤的有效弹光系数;对于一般的光纤材料,Pe可取0.22。
根据光纤光栅加速度传感器的定义,传感器的灵敏度S为FBG中心波长漂移值Δλ与加速度a之比,可表示为
(7)
将各参量带入式(7),可得传感器灵敏度的理论公式为
(8)
根据传感器的力学模型,对其固有频率进行分析。如图2所示,质量块可以被认为是一根摇杆,并且以铰链为中心上下摆动,设质量块绕铰链的转动惯量为J,按照能量法,可建立系统的动力学方程为
(9)
由式(9)得系统的固有频率为
(10)
由材料力学得,转动惯量J为
(11)
1.3 温度自补偿原理分析
在实际测量中,温度和应变能够同时引起FBG中心波长的变化。因此,在实际的应用中必须解决温度与应变的耦合问题,这样才能保证测量信号的准确性。结合柔性铰链的结构特点,采用双光栅温度补偿方式来消除温度的影响。当温度和应变同时存在时,假设外界温度变化为ΔT,则FBG1和FBG2的波长变化量分别表示为:
Δλ1=(1-Pe)ε1λ1+KT1ΔTλ1
(12)
Δλ2=(1-Pe)ε2λ2+KT2ΔTλ2
(13)
式中:ε1,ε2分别为FBG1和FBG2的轴向应变;KT1,KT2分别FBG1和FBG2的温度灵敏度系数。
由于2个FBG的材料相同、参数相近且呈对称粘贴,当质量块带动2个FBG时,一个拉伸,一个压缩,故FBG1和FBG2产生的应变大小相等、方向相反,即ε1=-ε2=ε。又因为所选的2个FBG的参数相近,即有λ1≈λ2=λ且KT1=KT2。
联立式(12)、式(13),得到2个FBG的波长差为
Δλ=Δλ1-Δλ2=2(1-Pe)λε
(14)
由式(14)可知,波长变化量与温度无关,采用双光栅的设计消除了温度的影响,同时提高了传感器的灵敏度,达到了增敏的效果。
2 有限元仿真分析
传感器的振动特性与传感器的固有频率密切相关,为了满足实际的测量需求,需要对传感器的结构参数进行优化。由理论分析的结果看出,加速度传感器灵敏度S和固有频率f与柔性铰链的半径R、最小厚度t、质量块的长b和高h密切相关。结合结构自身设计和边界尺寸约束,采用数值优化方法得到表1中的参数值,将表1中数据代入式(8)和式(10),计算得到传感器理论灵敏度为136.4 pm/g,固有频率为783 Hz。

表1 加速度传感器结构参数
为了研究传感器的振动特性,使用ANSYS对其敏感结构进行模态分析。首先,通过Solidworks建立传感器的三维模型,然后将三维模型导入到ANSYS软件中,按照表1所列参数设置材料属性,完成网格划分。随后,在传感器的基座施加固定约束,在忽略光纤作用力的情况下,得到传感器一阶模态位移云图。如图3所示,该传感器的一阶模态振型为沿x轴方向的纵向振动,其固有频率为733.93 Hz。与理论计算的结果基本一致。如图4所示,传感器的二阶模态振型为沿z轴方向的横向振动,其二阶固有频率为2 639.9 Hz。由此可知传感器横向振动固有频率远远超过主振型的固有频率,故该传感器的抗横向干扰的能力良好。

图3 传感器一阶模态位移云图

图4 传感器二阶模态位移云图
3 实验结果及分析
将所设计的加速度传感器进行实验研究。首先将传感器固定在振动台上,输出信号由光缆接入到解调仪的通道中,解调仪通过USB连接到计算机上,并由解调仪的软件读出传感器的波长值,同时由一个标准的电类加速度传感器作为参考信号,并且控制振动台的输入。实验中的振动台为丹麦B&K公司生产的振动测试系统;解调系统采用FGD-2000解调仪,工作波长变化范围为1 528~1 568 nm,测量分辨率为1.0 pm,采样频率为2 kHz。
3.1 幅频响应测试
在传感器的幅频响应测试中,将传感器固定在振动台上,施加1g的正弦激励信号,激励信号的频率以100 Hz为步长,从50 Hz开始增加至900 Hz,测量在不同频率下的2个FBG的波长之差。当双光栅的波长差值的峰值开始出现在700~900 Hz之间,再进一步细分,从700 Hz开始增加,以50 Hz为步长,得到的幅频曲线如图5所示。由图5得出加速度传感器的固有频率在800 Hz左右。幅频曲线在400 Hz以下的平坦度较好,即传感器的工作频率在400 Hz以下。

图5 传感器幅频响应测试曲线
3.2 传感器灵敏度测试
在传感器的灵敏度测试中,由于采用双光纤光栅对称布置的结构,所以选择2个FBG的波长差作为传感器的输出响应。通过振动台给加速度传感器分别施加50、80、100 Hz的正弦激励信号,以0.5g的加速度值为步长,加速度值增加至3g,分别得到3种频率下加速度值与波长差的关系曲线如图6所示。由图6得,2个FBG的波长差与加速度值具有良好的线性关系,分别对其进行线性拟合。拟合结果表明,传感器在50、80、100 Hz的灵敏度分别为131.6、134.8、138.1 pm/g,平均值为134.8 pm/g。与理论分析值的偏差为1.18%。

图6 传感器灵敏度测试曲线
3.3 温度自补偿测试
为了研究加速度传感器的温度自补偿性能,使用高温恒温试验箱对传感器进行了实验。实验中,将传感器放置在高温恒温试验箱中,调节高温恒温试验箱的温度从30 ℃到80 ℃,每次递增10 ℃为一个步长。分别测得不同温度测试点时2个FBG的中心波长值,从而得到FBG1和FBG2的温度响应曲线如图7所示。实验结果表明,FBG1和FBG2的中心波长均与温度之间成线性关系,拟合得到FBG1和FBG2的温度灵敏度系数KT1=24.3 pm/℃和KT2=24.2 pm/℃,线性相关系数均在0.999以上。2个FBG的灵敏度系数基本相等,故该传感器具有良好的温度自补偿能力。

图7 双光栅温度响应曲线
3.4 横向抗干扰测试
由于文中所设计的加速度传感器测量方向为单维,因而需要对其横向抗干扰能力进行测试。测量时可选取FBG1为研究对象,以传感器的敏感方向为主向,与敏感方向垂直的方向为横向。首先将传感器按照测量方向分别固定在振动台上,并施加频率为50 Hz,加速度幅值为1g的激励信号,分别得到传感器主向和横向的时域图如图8所示。由图8得出,传感器主向的波长变化量为49.3 pm,而横向的波长变化量小于2 pm。由此得出传感器的横向干扰度小于5%,其横向抗干扰性能良好。

图8 传感器横向抗干扰测试曲线
4 结论
文中设计了一种基于双光纤光栅的柔性铰链加速度传感器。该传感器采用双栅对称结构的设计方式,在提高灵敏度的同时又具有温度自补偿能力。另外,对传感器的结构进行理论分析和有限元仿真,并通过实验研究了传感器的工作性能。结果表明,传感器的固有频率约为800 Hz,灵敏度为134.8 pm/g,横向抗干扰度小于5%,具有良好的温度自补偿能力,并且理论计算和实验的结果基本一致。

