平面线圈型时栅传感器及动尺姿态误差特性分析
刘 洋,武 亮,彭东林,钟自强,牟 川,景 欢
(重庆理工大学机械检测技术与装备教育部工程中心,重庆 400054)
0 引言
时栅位移测量方法是通过在测量范围内构建匀速运动坐标系,将空间量转换为时间量,采用高频时钟脉冲作为测量基准实现精密位移测量[1-7]。原有的直线式时栅传感器通过在导磁体上通过线切割切出齿槽,在槽内嵌入励磁绕组的方法产生行波磁场[8-11]。以此作为匀速运动坐标系,然而齿槽变化将引起磁场运动速度非线性变化,由此引入谐波误差影响测量精度。传感器动尺和定尺的非理想安装状态会进一步致使位移测量精度下降。
针对上述问题,本文提出一种基于平面线圈的直线时栅位移传感器,规避了齿槽结构对测量精度的影响,然后通过仿真分析对动尺在不同姿态下传感器的误差进行了分析并通过实验对其展开验证。为传感器实现高精度位移测量提供了新的解决思路。
1 传感器工作原理
1.1 传感器结构
如图1所示,传感器由定尺和动尺2部分组成,定尺包含导磁基体和正余励磁线圈,动尺包含磁场拾取线圈和导磁基体,励磁线圈和磁场拾取线圈均采用回型平面线圈。正余弦激励线圈沿测量方向相互交错排列,各自有偶数个回型线圈“正反正反”相互串联,磁场拾取线圈由2个回型线圈沿测量方向“正反”串联组成。相邻两个励磁线圈中心距为0.25W,相邻两个磁场拾取线圈中心距为0.5W,其中W为空间节距。
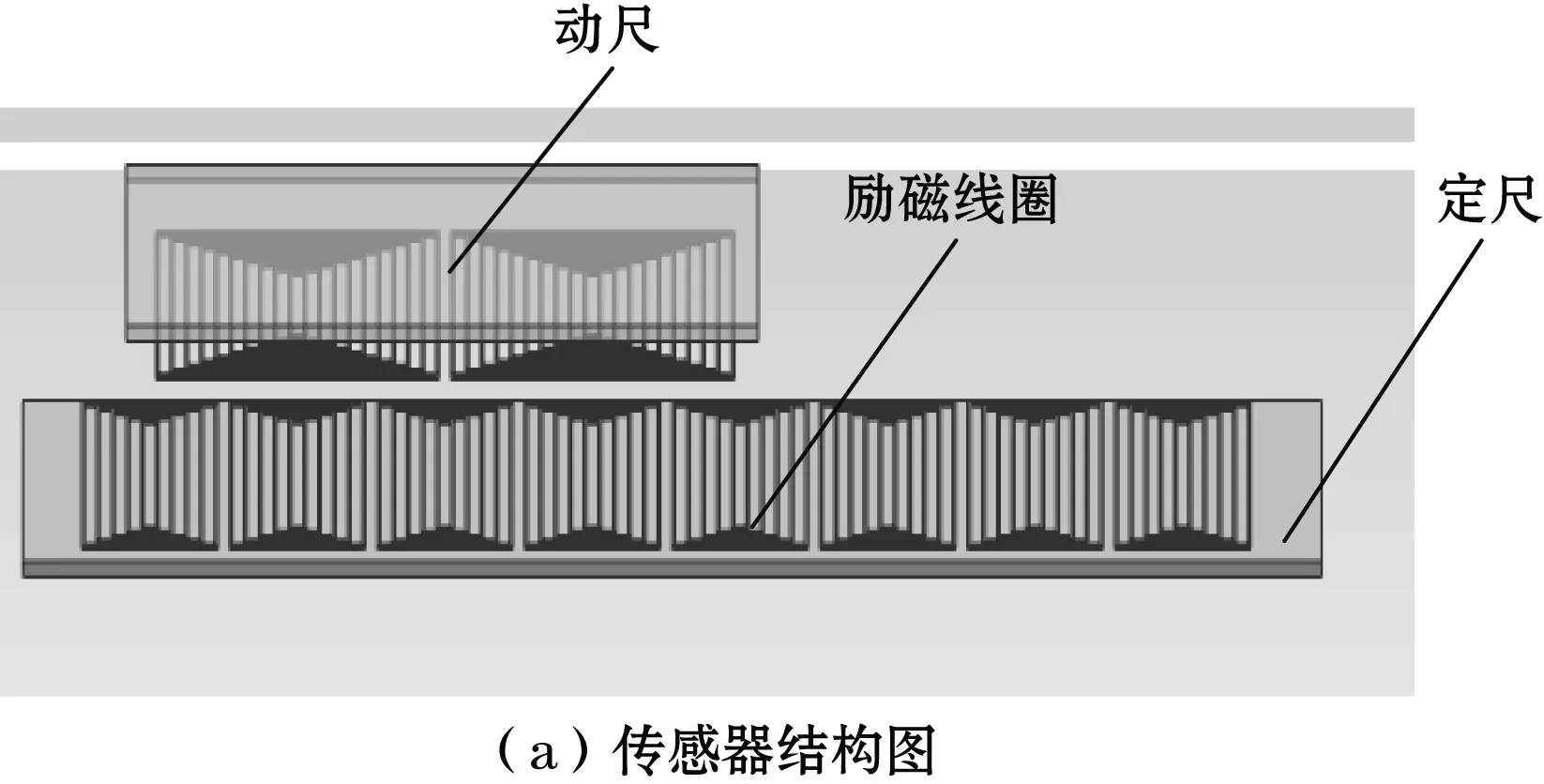

图1 传感器结构示意图
1.2 传感器测量原理
回型励磁线圈产生的磁场为每匝线圈产生的磁场矢量叠加,而每匝线圈产生的磁场为4段导线产生的磁场相叠加。磁场计算过程如图2所示。

图2 回形线圈磁场计算模型
根据毕奥萨伐尔定律,通电导线周围产生的磁场可以看作是由电流元沿导线电流方向产生磁场强度的积分[12]。若通入电流I,单根通电直导线周围产生的磁场强度在空间一点P处的表达式为
(1)

磁场B的方向由右手螺旋定则确定且与导线所在平面垂直,对于单个线圈产生的磁场可看作LAB、LBC、LCD、LDA 4根通电导线在P点处产生的磁场相叠加。根据式(1)单根导线在P点处磁场强度为

(2)
式中:2a为线圈边长;x、y、z为P点空间坐标。
同理可得BLBC,BLCD,BLDA,那么单个线圈在P点处产生的磁场强度可表示为
B=BLAB+BLBC+BLCD+BLDA
(3)
回形线圈在P点处产生的磁场强度B1可表示为
(4)
回形线圈产生的磁场呈周期性变化,其变化周期为传感器空间节距W,用傅里叶级数展开可表示为
(5)
式中:n为线圈匝数;j为谐波次数;Pj为第j次谐波初相角;φ0为磁通量的直流分量;φj为第j次谐波分量的幅值。
当正余弦分别通入交变励磁电流Is=Imsinωt,Ic=Imcosωt。此时正余弦励磁线圈产生的磁通量分别为:
(6)
(7)
式中:W为传感器节距;PJ为第J次谐波的相位。
感应电动势可由两者相互叠加得到,由法拉第电磁感应定律可得到其大小为

(8)
式中:ω为励磁电流频率;W为传感器节距;x为位移量;P1为基波相位。
感应信号的频率与励磁信号频率相同,但是相位是不同的。行波磁场作为运动坐标系故两者的运动速度相等且为v=Wω/(2π),在信号处理的后续阶段采用高频时钟脉冲计算时间差Δt[13-16]。位移表达式可表示为
x=v·Δt
(9)
式中:x为位移量;v磁场运动速度;Δt为时间差。
2 动尺不同姿态下建模仿真与误差分析
在使用传感器进行位移测量时应保证定尺、动尺及测量方向相互平行,然而在传感器重复安装过程中,动尺与定尺之间间隙的重复性难以保证。在传感器使用时动尺姿态会出现几个方向的变化,本文将测量方向定义为x轴方向,在测量平面上与x轴垂直的方向为y轴,垂直于测量平面的方向为z轴。把动尺绕x轴旋转称为滚转,沿y轴旋转称为俯仰,沿z轴旋转称为偏摆,把动尺沿y轴方向移动称为偏移。针对动尺不同姿态进行建模仿真,分析各个姿态变化时的误差特性从而可以有效地指导传感器的安装及后续的误差分析。
2.1 建模参数及相关设置
AnsysMaxwell是一款具有强大的电磁场分析处理和求解功能的软件,广泛应用于电磁场分析及工程领域[9]。本文利用该软件建立了动尺在各姿态下的仿真模型,进行有限元分析。模型的几何相关参数如表1所示。

表1 仿真模型参数表
动尺相对于定尺沿x轴移动距离设置为一个空间节距即20 mm,从0 mm开始步距为0.5 mm仿真结果得到动尺在一个节距为40个不同空间位置的感应信号波形图,即40条相位不同的正弦波,每一条正弦波沿时间展开其周期设为25 μs、步距为1 μs,即每条正弦波在时间轴上采样25个点。当动尺相对于定尺沿测量方向移动一个空间节距时,仿真结果中40条正弦波形对应的初相角变化一周期即为360°。
2.2 偏移姿态下误差特性仿真分析
一般来说为了消除边缘效应,定尺宽度会大于动尺宽度,因此动尺相对于定尺沿y轴偏移对输出感应信号影响较小,因此本文主要讨论动尺沿z轴偏移,其本质上是改变了定尺与动尺之间的气隙厚度,图3为动尺相对定尺在不同气隙厚度下传感器磁场拾取线圈输出的感应信号。

(a)d=0.1 mm电动势
比较图3中的输出信号幅值可知:动尺相对于定尺沿z轴偏移的距离(气隙厚度)越大,感应信号幅值越小。为了分析气隙厚度的变化对传感器输出信号误差特性影响。首先计算不同气隙厚度下各条正弦曲线的初相角,然后与理论初相角作差得到动尺在空间位置的相角误差,再将相角误差转换为位移误差,如图4所示。
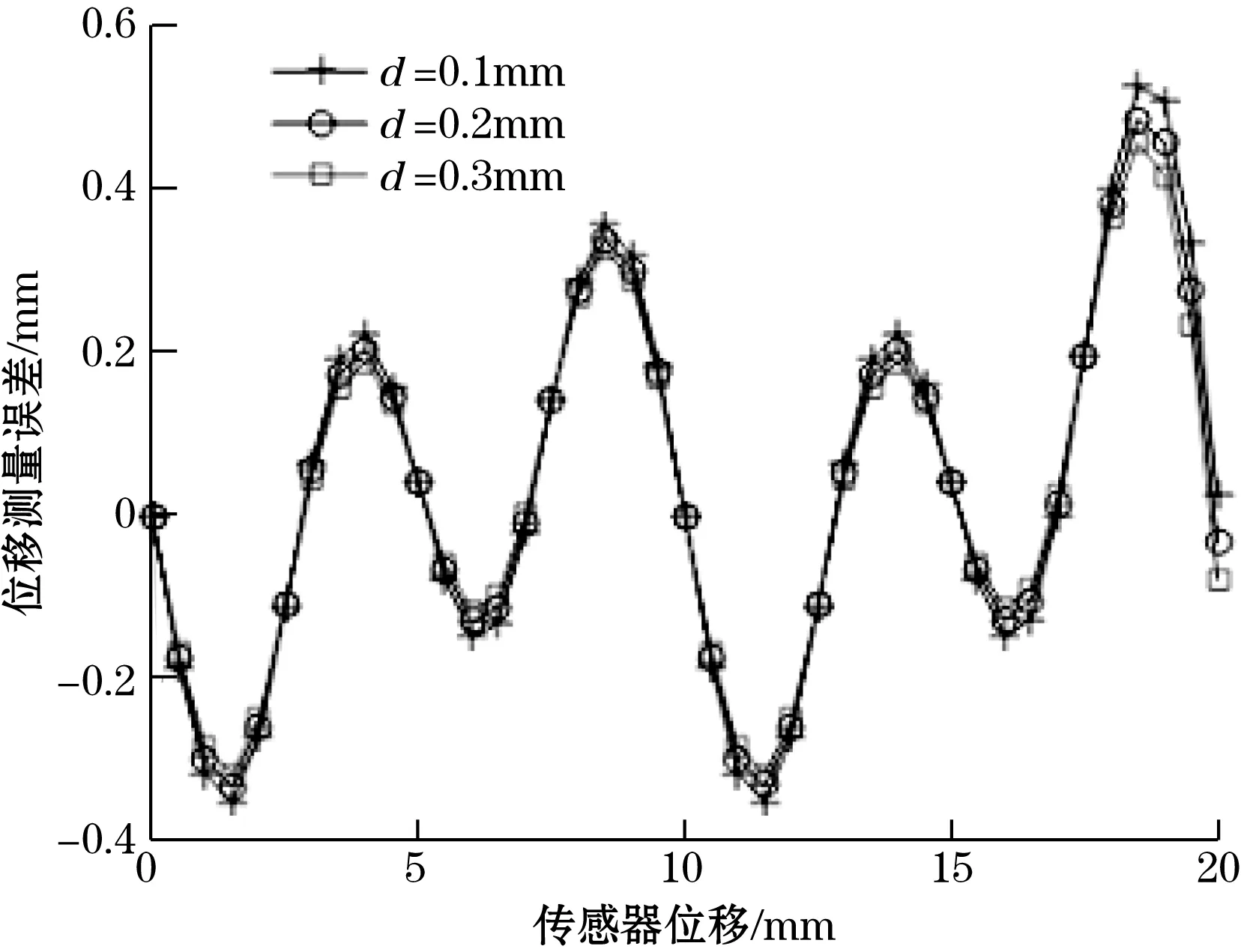
图4 不同气隙厚度测量误差
由图4可知当动尺与定尺之间的气隙厚度发生变化时其位移误差规律基本一致,均以4次误差为主。当气隙厚度为0.1 mm时,磁场拾取线圈输出感应信号峰峰值为17 V,位移误差峰峰值约为0.877 mm;当气隙厚度为0.2 mm时,磁场拾取线圈输出感应信号峰峰值为15 V,位移误差峰峰值约为0.818 mm;当气隙厚度为0.3 mm时,此时磁场拾取线圈输出感应信号峰峰值为12.5 V,位移误差峰峰值约为0.773 mm。由此可知当动尺与定尺之间的气隙为0.2 mm时,不仅能获得较强的输出信号,而且不会产生较大的误差。
2.3 俯仰姿态下误差特性仿真
动尺的俯仰姿态就是动尺相对于定尺绕y轴旋转了一定角度,而定尺则保持原状态。这样就使得动尺与定尺之间不再是平行关系而是存在一定角度。此时输出的感应信号幅值会发生变化,引入谐波误差。在实际安装中通常把俯仰的角度与在z轴方向上高度H1变化对应起来,如图5所示。

图5 俯仰示意图
z方向的高度H1分别取20、40 μm,且动尺与定尺最小气隙厚度为0.2 mm时,传感器磁场拾取线圈的输出仿真信号如图6所示。
《能源生产和消费革命战略(2016—2030)》等政策出台 推动油气行业拥抱能源革命 田磊,苏铭 1 20
(a)H1=20 μm电动势
计算图中每条正弦波的初相角和初相角误差并将其换算为测量误差,如图7所示。

图7 俯仰位移测量误差
由于动尺与定尺在x轴方向上存在一定夹角时会产生俯仰,引入较大的谐波误差。当H1=20 μm时位移测量误差的峰峰值约为0.403 5 mm,当H1=40 μm时位移测量误差的峰峰值约为0.398 2 mm。由此可得出俯仰越大引谐波误差量就越大。
2.4 偏摆姿态下误差特性分析
偏摆即动尺相对于定尺绕z轴旋转一定角度。这种情况也会使输出的感应信号幅值发生变化,引入谐波误差。在实际安装过程中通常把动尺沿z轴的偏摆与沿y轴方向的距离H2对应起来,如图8所示。

图8 偏摆示意图
图9为H2分别取20、40 μm,拾取线圈时输出的感应信号且动尺与定尺最小的气隙厚度为0.2 mm。

(a)H2=20 μm电动势
计算每条正弦波的初相角以及初相角误差并换算为位移测量误差,如图10所示。

图10 不同偏摆位移测量误差
2.5 滚转姿态下的误差特性仿真
滚转即为动尺相对于定尺绕x轴旋转了一定角度。此时传感器输出的感应信号幅值发生变化,引入谐波误差。在实际安装中通常把滚转的角度与在z轴方向上高度H3变化对应起来,如图11所示。

图11 滚转示意图
图12为动测尺和定尺最小气隙厚度为0.2 mm时,不同滚转姿态下模型的仿真结果。

(a)H3=20 μm电动势
计算每条正弦波的初相角以及初相角误差并转化为位移测量误差如图13所示。

图13 不同滚转位移测量误差
由图13可知,动测头和定尺不平行会产生安装滚转,位移测量产生的附加误差也极小。当H3=20 μm时,位移总误差的峰峰值约为0.407 9 mm,当H3=40 μm时,位移总误差的位移总误差的峰峰值为0.403 5 mm。
2.6 动尺不同姿态下误差特性比较
为了能够更进一步研究动尺在不同姿态下的误差特性,把不同姿态下的测量误差进行傅里叶变换,得到各次谐波的幅值和相位。截取幅值和相位较大的频次前五次进行比较分析,如表2所示。
由表2可知动尺在俯仰情况下会使1次和2次误差增加较大,当H1=20 μm时,测量误差的1次增加量为0.8 μm,2次增加量为5 μm;当H1=40 μm时,测量误差1次增加量为1.6 μm,2次增加量为8.8 μm,由此可得出俯仰角越大,1次、2次误差增加量就越大。动尺的偏摆和滚转姿态下引起各次误差变化较小。

表2 动尺不同姿态下主要误差频次的幅值相位比较
3 实验验证与分析
加工并制作了传感器样机,结构参数与第三节阐述的仿真模型参数一致。传感器的定尺与动尺都采用PCB工艺加工而成,励磁线圈与磁场拾取线圈采用PCB走线工艺在定尺和动尺上进行加工。导磁基体采用45#钢进行加工并对基体表面进行研磨处理以此来安装定尺与动尺。
安装传感器并搭建如图14所示的实验平台,传感器、滚珠丝杆、光栅尺平行排列在大理石平台上。动尺与丝杆螺母刚性连接伺服电机通过联轴器带动丝杆转动,从而使得传感器动尺与光栅读数头同步运动。通过信号采集电路对传感器及光栅数据进行同步采集并通过串口发送至上位机进行对比。

图14 搭建实验平台图
3.1 实验验证
实验中首先安装好定尺,以保证动尺与定尺在不同气隙厚度下的误差特性,安装动尺时应保证俯仰不超过4 μm、偏摆不超过4 μm、滚转不超过2 μm。然后调节动尺与定尺的气隙厚度分别为0.1、0.2、0.3 mm。图15为传感器移动一个空间节距W=20 mm的测量数据与光栅头读数对比后的结果。

图15 不同气隙厚度下位移误差实验数据
调整动尺与定尺的气隙厚度为0.2 mm。然后调节动尺沿z轴旋转使得偏摆距离分别为20 μm、40 μm,如图16所示。

图16 不同偏摆下测量误差
调整动尺沿x轴旋转使得俯仰距离分别为20 μm、40 μm。图17为传感器移动一个节距的测量数据与光栅读数头测量数据对比后的结果。

图17 不同俯仰下位移误差实验数据
调整动尺沿y轴的旋转距离使其滚转距离分别为20 μm、40 μm。图18为俯仰姿态下传感器移动一个空间节距的测量数据与光栅读数头对比后的结果。动尺在不同姿态下误差主要频次的幅值和相位如表3所示。

图18 不同滚转下位移误差实验数据

表3 动尺不同姿态误差频次的幅值相位比较
3.2 实验结果分析
通过对比表2和表3可知:
(1)气隙厚度越大,位移误差的1次、 2次、4次谐波的幅值越小;俯仰高度变大,位移误差1次、2次谐波幅值增加较大,但4次谐波幅值略微减小。相比较而言不同偏摆和滚转对测量误差影响较小,偏摆对2次误差影响相对稍大,滚转对各次误差影响较小。
(2)位移误差除去1次、2次、4次谐波外,其余各次谐波幅值均较小,与仿真结果相近。
4 结论
本文提出了一种新型的平面线圈型时栅直线位移传感器。并对传感器动尺不同姿态的误差特性进行了仿真研究并进行了实验验证。仿真和实验结果均表明,各种动尺姿态下,对位移误差的1次、2次、4次谐波影响较大,其中俯仰姿态下传感器引入的附加误差最大,而不同气隙厚度、偏摆、滚转姿态下引入附加误差相对较小。仿真与实验结果基本一致。本文为平面线圈型的磁场式直线时栅位移传感器提供了误差分析和理论模型,对基于平面线圈的时栅位移传感器后续研究具有重要意义。

