具有垂直传染和年龄结构的MSEIR传染病模型的稳定性

粟 丹，赵 春

（天津师范大学数学科学学院，天津 300387）

传染病的出现和传播会给人类的生存和发展带来严重威胁，因此建立恰当的数学模型来分析传染病的传播规律进而控制疾病的传播是十分重要的.垂直传染（指胎儿由母体得到疾病）作为一种特殊的疾病传播方式在维持疾病的延续中起着重要作用，目前对具有垂直传染和年龄结构的传染病模型的研究较少[1-3].文献[1]研究了具有垂直传染和年龄结构的SEIR传染病模型的稳定性.文献[2]研究了一类带有垂直传染的年龄结构SIR流行病模型的解的存在唯一性.文献[3]研究了带有垂直传染和具有年龄结构的接种流行病模型的解的存在性.

当母体感染某种传染病后，她体内将产生相应抗体，对处于潜伏期、染病期和已恢复的母体，她们所生育的子代在一个短暂时期内具有自然免疫力，称为被动免疫，当被动免疫消失后，子代则变成易感者.本文考虑在以往具有年龄结构的传染病模型[4-8]的基础上添加被动免疫，研究一类具有垂直传染和年龄结构的MSEIR传染病模型的稳定性.

1 模型建立

将人群分为被动免疫类、易感类、潜伏类、染病类和免疫类.M（a，t）、S（a，t）、E（a，t）、I（a，t）和R（a，t）分别表示被动免疫类、易感类、潜伏类、染病类和免疫类人群在t时刻年龄为a的人口密度.b（a）和 μ（a）分别表示与年龄相关的出生率和自然死亡率.[δ（a）]-1、[τ（a）]-1和[γ（a）]-1分别为平均被动免疫周期、平均潜伏周期和平均染病周期，不考虑因病死亡，κ1和κ2分别为E和I的垂直传染率.设传染病以混合比例方式传播，令水平传染力函数为

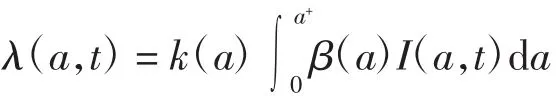
其中：a+＞ 0，k（a）为与年龄相关的接触率，β（a）为与年龄相关的染病率.

建立MSEIR模型为

其中Q=（0，T）×（0，a+），且初边值条件为

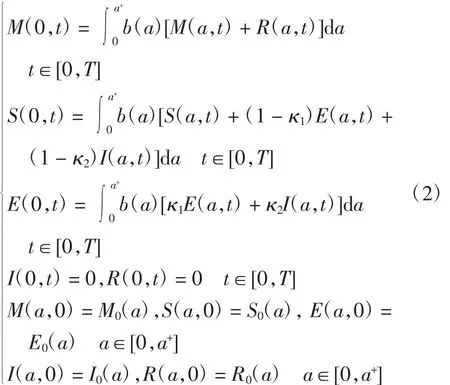
本文假设模型（1）～（2）满足如下条件：

（A1）b（a）、δ（a）、τ（a）、γ（a）、β（a）、k（a）∈L∞[0，a+]，且b（a）、δ（a）、τ（a）、γ（a）、β（a）、k（a）均非负.

（A2）M0（a）、S0（a）、E0（a）、I0（a）、R0（a）∈L1[0，a+]，且M0（a）、S0（a）、E0（a）、I0（a）、R0（a）均非负.

（A3）μ（a）∈L∞loc[0，a+]，μ（a）≥0，且

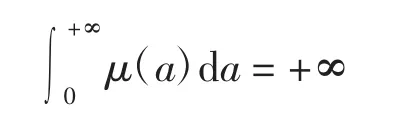
定义若（M，S，E，I，R）∈（L∞（0，T）；L1（0，a+））5在每条特征线a-t=l上都绝对连续，（a，t）∈Q，l∈R，且M、S、E、I、R满足式（1）及

则称（M，S，E，I，R）为模型（1）～（2）的解.

2 解的存在唯一性

令

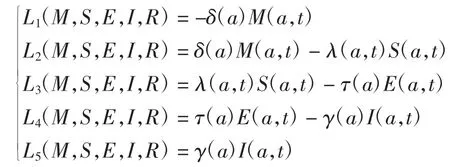
则模型（1）可写为

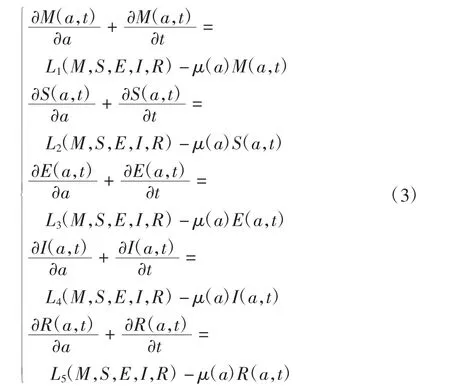
记（x1，x2，x3，x4，x5）=（M，S，E，I，R），定义解的空间为

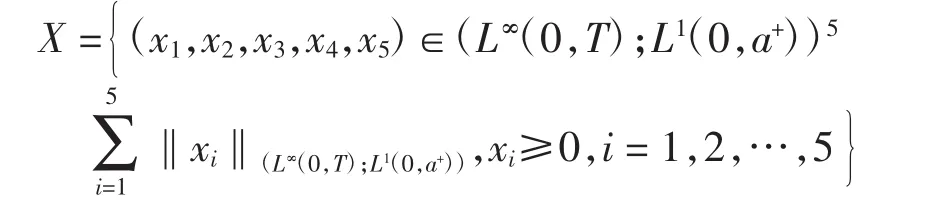
利用特征线法求解模型（3），可得

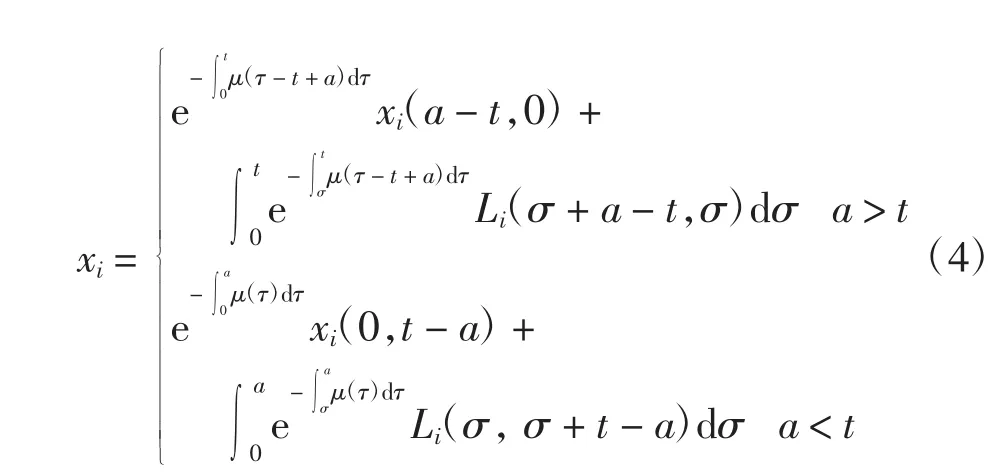
令

P（a，t）=M（a，t）+S（a，t）+E（a，t）+I（a，t）+R（a，t）则P（a，t）满足

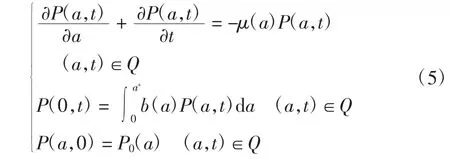
由文献[9]可知，存在常数

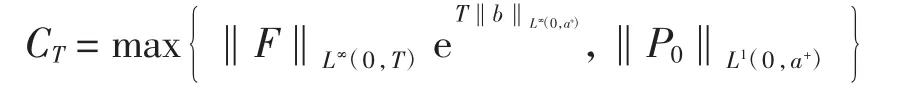
使得在（0，T）上几乎处处满足‖P（·，t）‖L1（0，a+）≤CT，其中

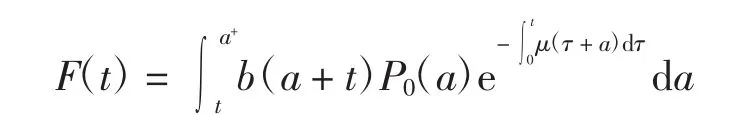
定理 1设条件（A1）~（A3）成立，则模型（1）~（2）在空间X中存在唯一解（M，S，E，I，R）.

证明定义映射Π：X→X及等价范数为

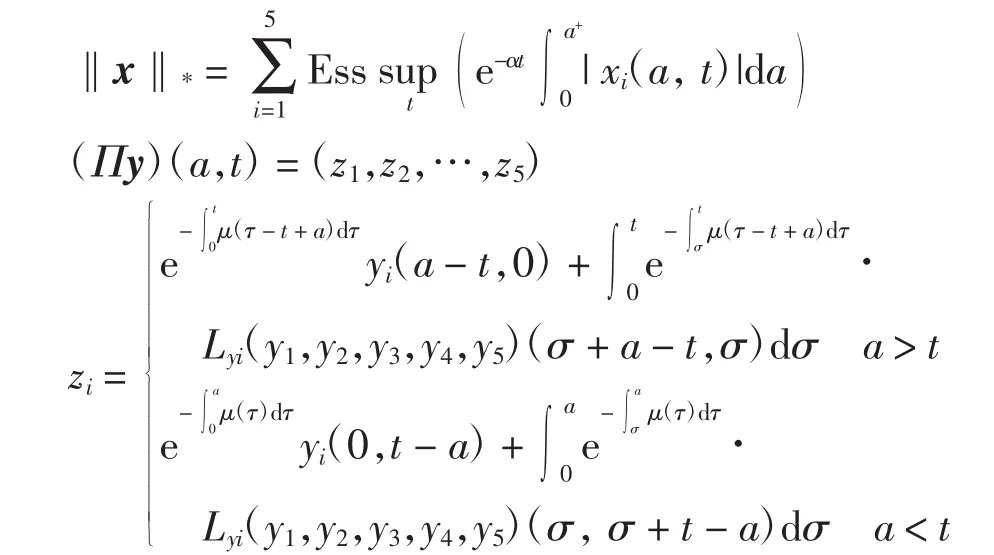
则对任意 y1、y2∈X，有

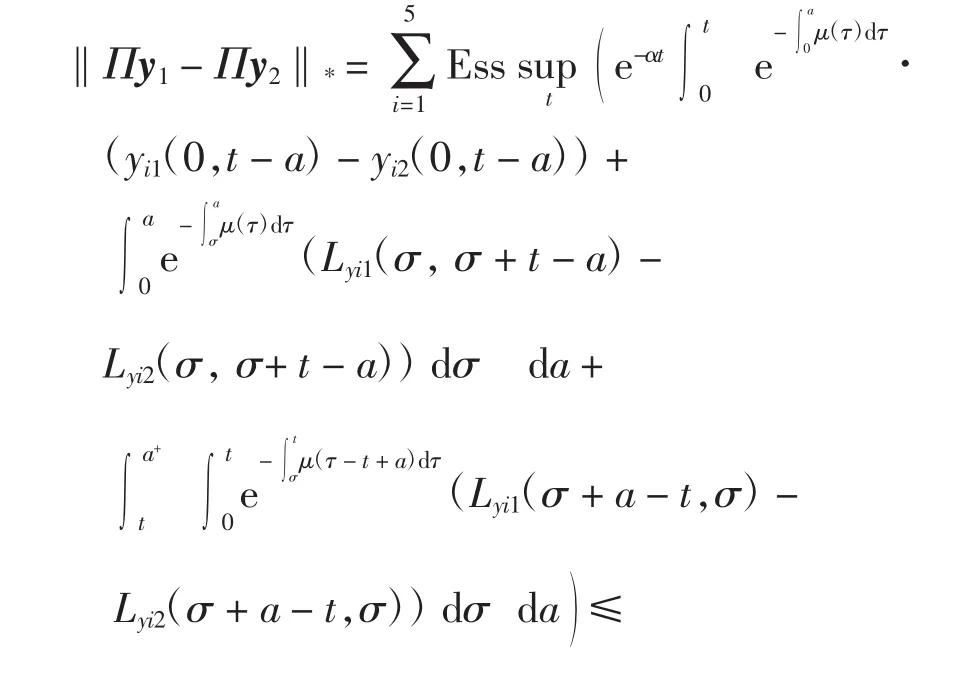
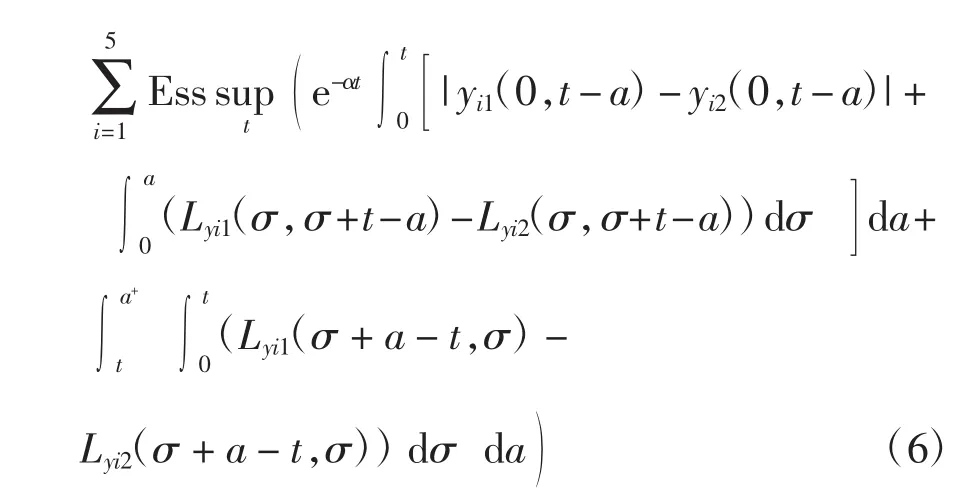
且有

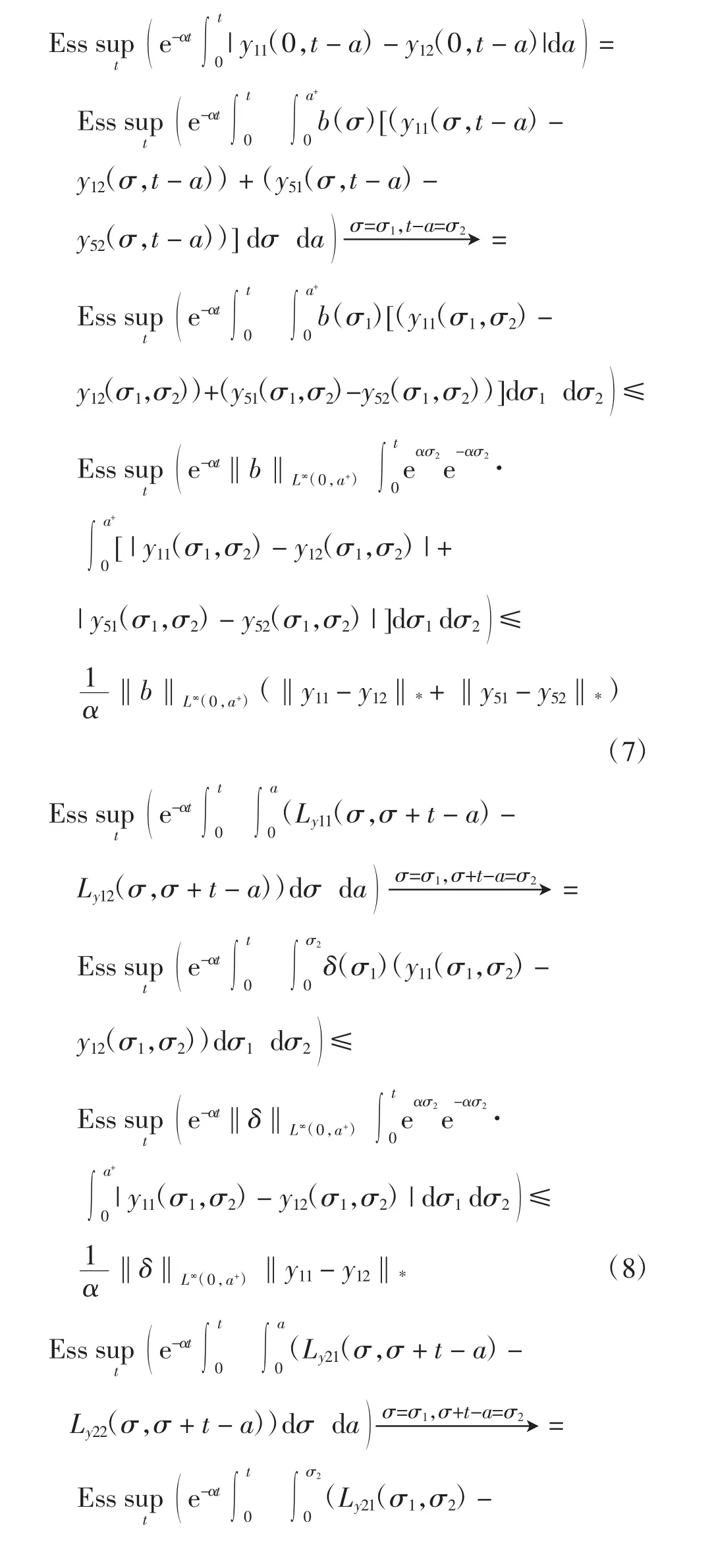
同理于式（7）可得

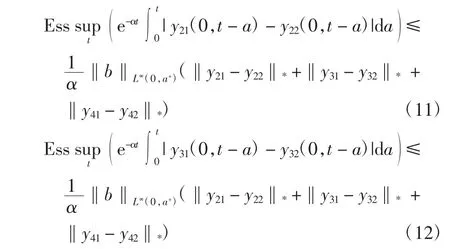
同理于式（8）~式（9）可得

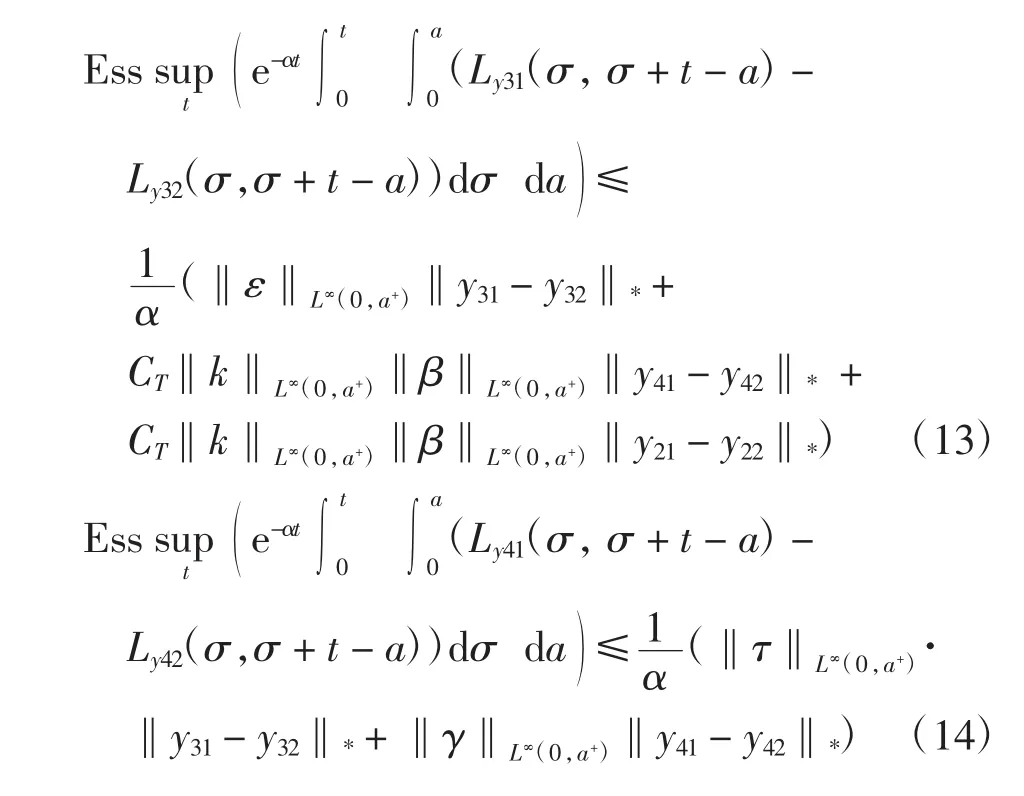
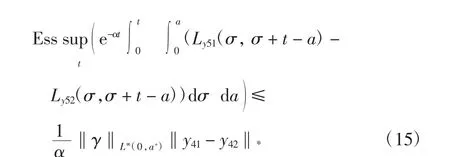
利用式（7）~式（15），结合式（6）可得

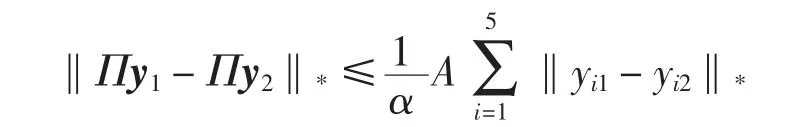
其中A是与‖δ‖L∞（0，a+）、‖τ‖L∞（0，a+）、‖γ‖L∞（0，a+）、‖β‖L∞（0，a+）、‖k‖L∞（0，a+）有关的常数.显然当 α＞A时，Π是X上的压缩映射，则Π存在唯一的不动点x0，即模型（1）~（2）存在唯一解 x0.证毕.

3 无病平衡点的稳定性

假设人群处于稳定状态，即

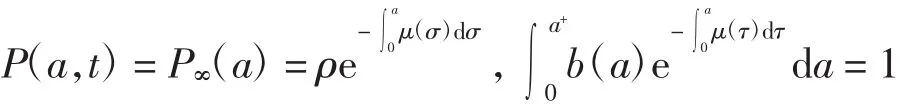
对模型（1）进行归一化变换，令

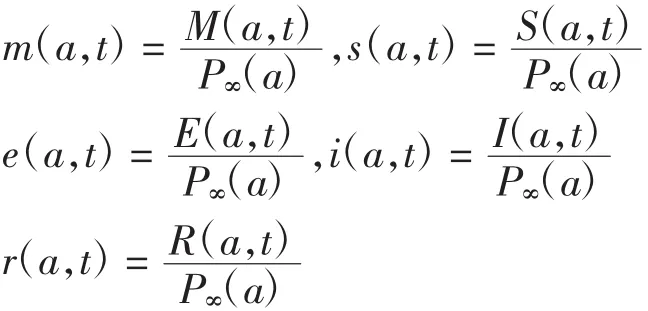
可得

模型（16）的平衡解满足

求解模型（17）得

显然，当β0=0时，由式（18）可得e（a）≡i（a）≡r（a）≡0，即存在无病平衡点

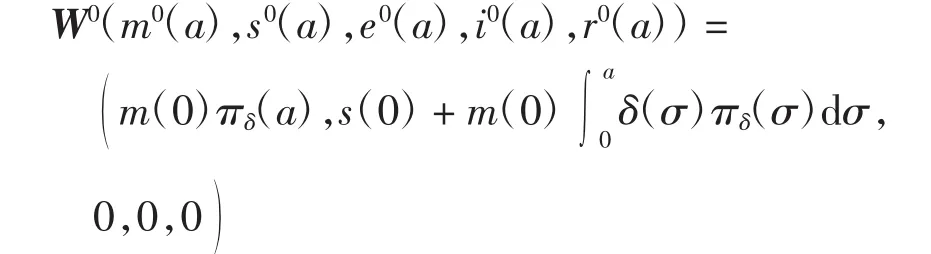
设模型（16）存在指数形式的解

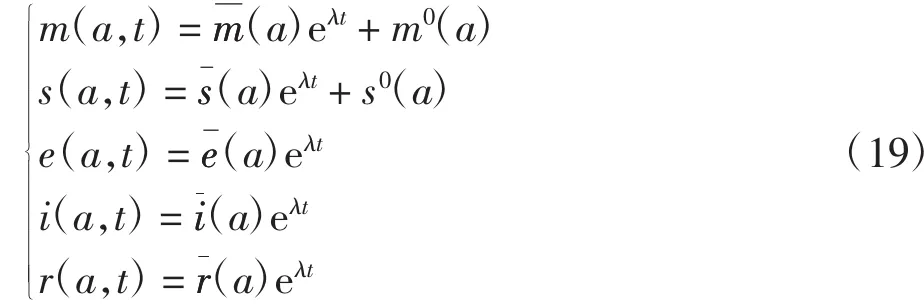
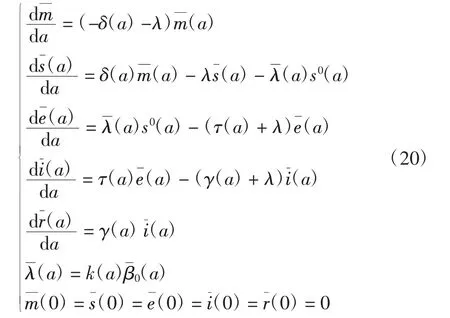
求解模型（20）得

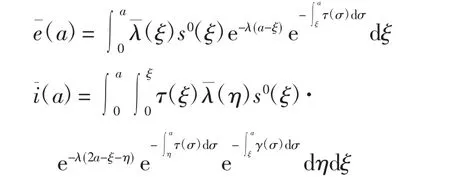
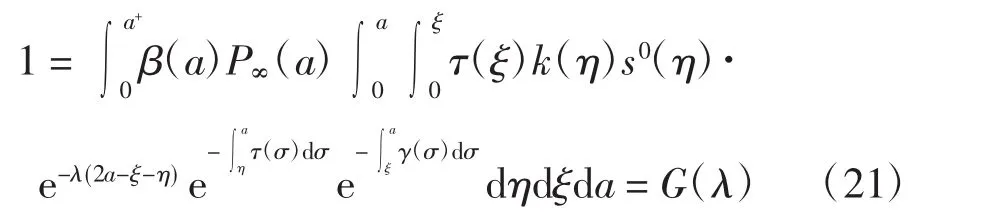
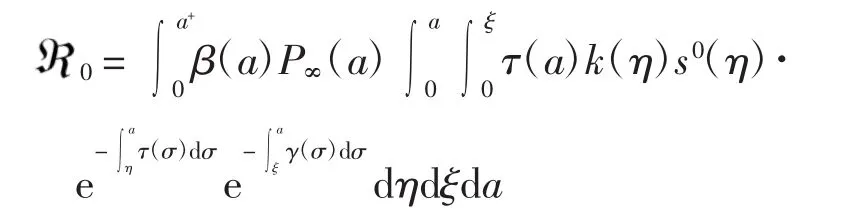
定理2若0＜1，则无病平衡点W（0m（0a），s（0a），0，0，0）是局部渐近稳定的；若0＞1，则无病平衡点是不稳定的.

证明显然G（λ）关于λ严格递减，且0.若0＜1，则特征方程（21）有唯一负实根 λ*，此时无病平衡点W0是局部稳定的.进一步，设λ=x+iy是方程（21）的任意一个复数根，x、y∈R，则由 1=G（λ*）=G（x+iy）≤G（x）可得 Re λ =x≤λ*，即 W0是局部渐近稳定的.若0＞1，则存在唯一正常数λ*满足方程（21），即特征方程（21）有唯一的正实根，此时无病平衡点W0不稳定.证毕.