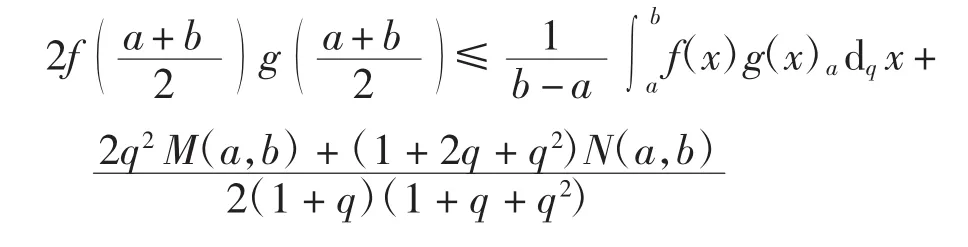区间凸函数的量子积分Hermite-Hadamard型不等式
娄天依,叶国菊
(河海大学理学院,南京 210098)
量子微积分又称为q-微积分,量子微积分没有极限的概念,它是一类基于有限差分重标思想提出的现代微积分.近些年,量子微积分在组合数学、数论、量子力学及相对论等科学领域中发挥着重要作用,引起了学者的广泛关注.
2002 年,Kac 等[1]引入了q-导数、q-原函数和q-积分的相关概念,并给出了一些相关性质.此后,关于量子微积分的研究成果日益增多[2-6],其中,文献[6]引入了连续函数f:[tk,tk+1]→R 的qk-导数和qk-积分的概念,并讨论了该积分的重要性质,同时给出了量子微积分在脉冲微分方程中的应用.作为量子微积分理论的重要组成部分之一,量子积分不等式也受到众多学者的关注,如,文献[7]将一些经典不等式与量子积分相结合,得到了q-Hölder、q-Hermite-Hadamard等量子积分不等式.关于量子积分不等式的更多结果可参阅文献[8-10].
另一方面,自1960年代以来,区间分析理论作为一种解决不确定性问题的重要方法被广泛应用.近些年,一些学者将经典不等式推广至区间值函数的情形,得到了关于区间值函数的Minkowski不等式[11]、Jensen 不等式[12]、Hermite-Hadamard 不等式[13]等.
受以上文献启发,本文引入区间值函数量子积分的概念,利用区间h-凸函数得到了若干区间值函数量子积分Hermite-Hadamard型不等式,所得结论推广了文献[7]和文献[14]中的一些结果.
1 预备知识
设Kc(R)为R上非空紧凸集构成的空间,即实数u和分别为[u]的左端点和右端点.若,则称[u]为正的;若,则称[u]为负的.Kc+(R)(Kc-(R))表示正(负)区间构成的集合.当时,称[u]为退化区间.
设 λ∈R,对于K(cR)中的元素和其四则运算如下:
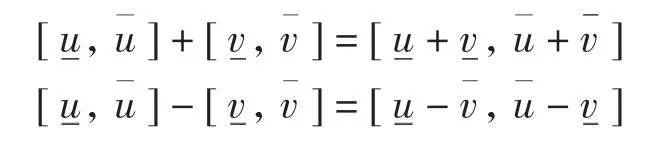
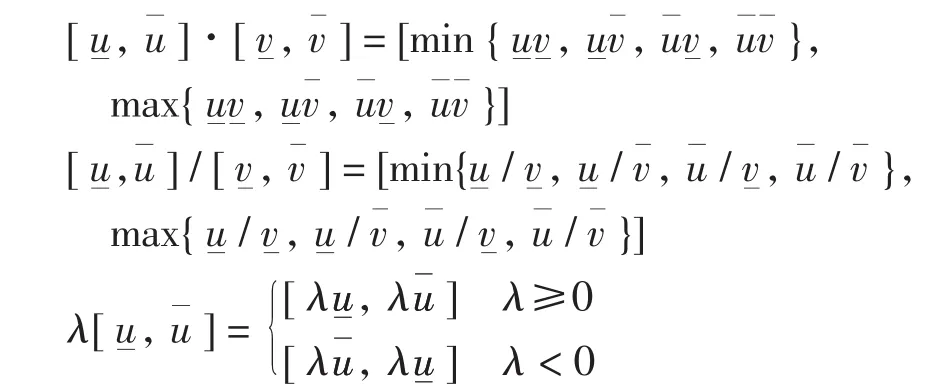
定义包含关系“⊆”为
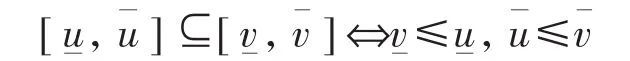
设J=[a,b]⊂R为一个区间,f:J→Kc(R)为一个区间值函数,记,其中和是J上的实值函数,且对任意x∈[a,b]有
定义1[15]设h:[c,d]→R为一个非负函数,(0,1)⊆[c,d]且h≢0.若f(x):J→R是非负的,且对任意x、y∈J,t∈[0,1],有
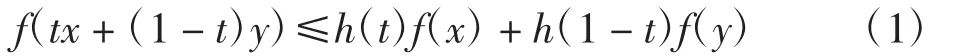
则称f(x)为J上的h-凸函数,用SX(h,J,R)表示J上所有h-凸函数构成的集合.若式(1)中不等号反向,则称f(x)为J上的h-凹函数,用SV(h,J,R)表示J上所有h-凹函数构成的集合.
定义 2[13]设h:[c,d]→R 为一个非负函数,(0,1)⊆[c,d]且h≢0.若区间值函数f:J→Kc+(R)满足
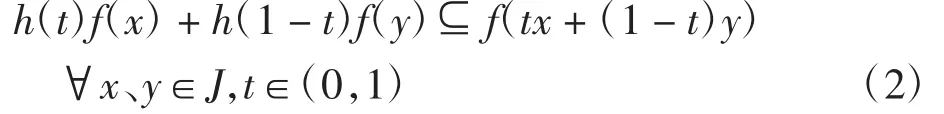
则称f为J上的区间h-凸函数.若式(2)中包含符号反向,则称f为J上的区间h-凹函数.用SX(h,J,Kc+(R))(SV(h,J,Kc-(R)))表示J上所有区间h-凸(h-凹)函数构成的集合.
定义3[1]设q为常数,且0<q<1,f:J→R为连续函数,若对任意x∈J,有

则称aDqf(x)为f(x)在x∈J处的q-导数.若对任意x∈J,aDqf(x)都存在,则称f(x)在J上是可微的.
注1若a=0,则有0Dqf=Dqf,其中Dqf(x)=即为q-Jackson导数.
定义4[1]设f:J→R为连续函数,称
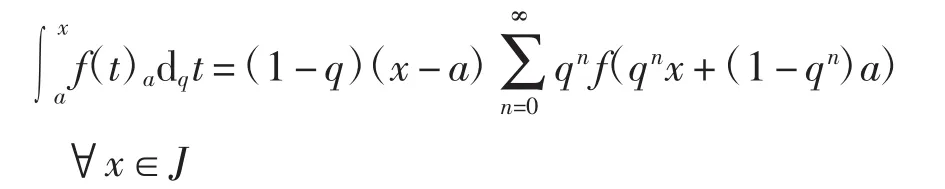
为f在J上的q-积分.用q([a,b])表示J上所有q-可积实函数构成的集合.若c∈(a,x),则有
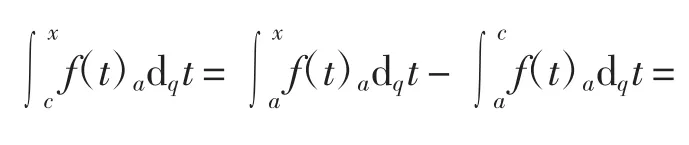
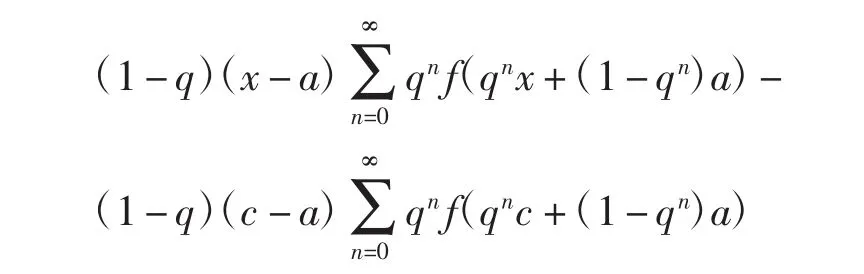
注2若a=0,则有f(qnx),∀x∈[0,∞),这即为q-Jackson积分.
定理1[6]设f:J→R为连续函数,则有
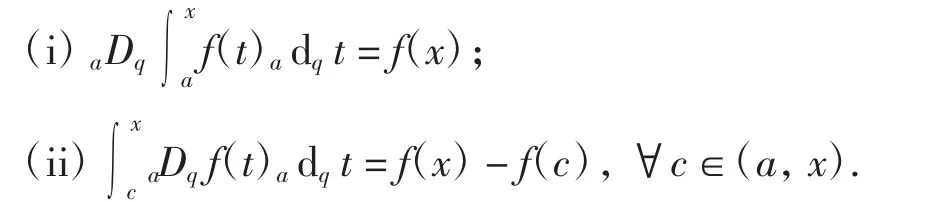
定理2[6]设f、g:J→R为2个连续函数,α∈R,则对任意x∈J,有
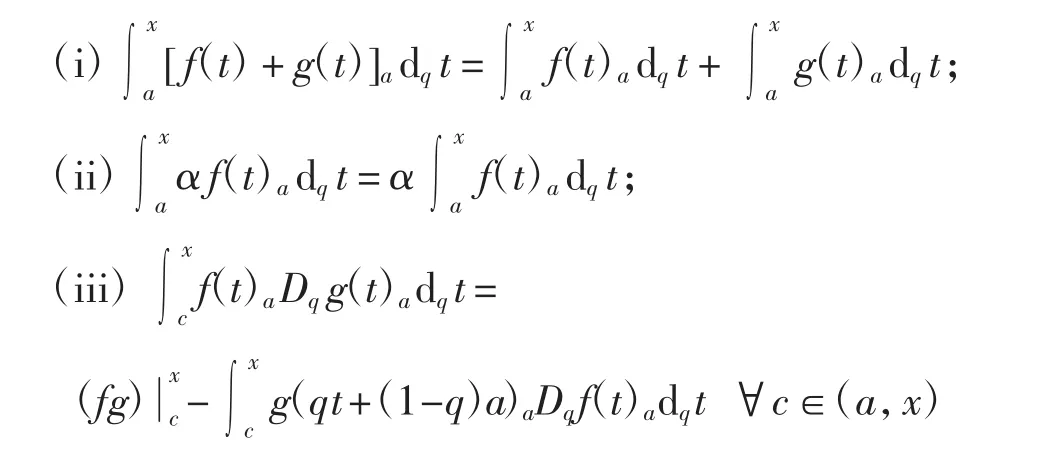
2 主要结果
定义5设f:J→Kc(R)为区间值函数,若
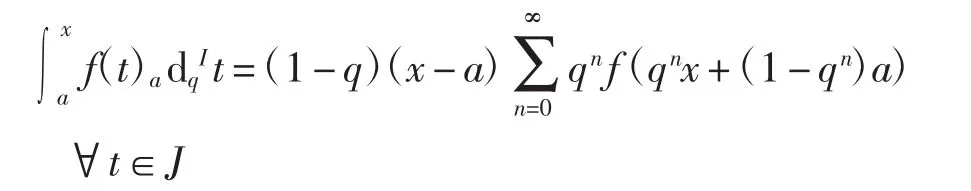
则称f在J上是Iq-可积的.用Iq([a,b])表示J上所有Iq-可积的区间值函数构成的集合.
由定义5易得定理3.
定理3设f:J→Kc(R)为区间值函数,f(x)=则f在J上是Iq-可积的当且仅当和在J上是q-可积的,且
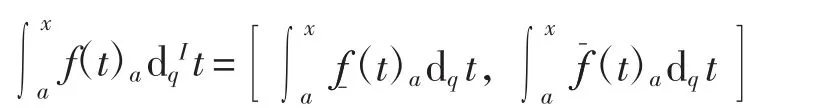
定理4设f:J→Kc(R)为一个区间h-凸函数,且非负,且h(1/2)≠0.若则有
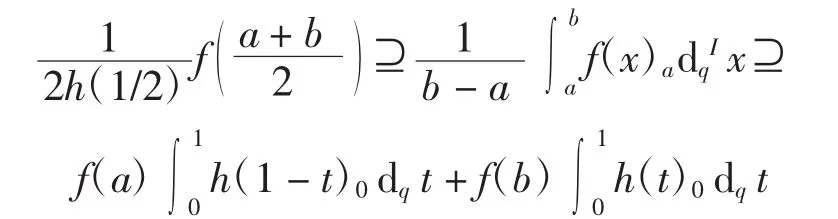
证明由区间h-凸函数的定义可得
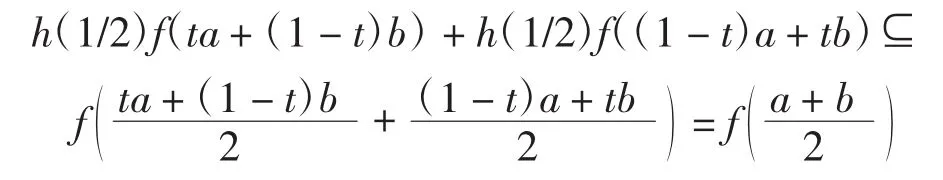
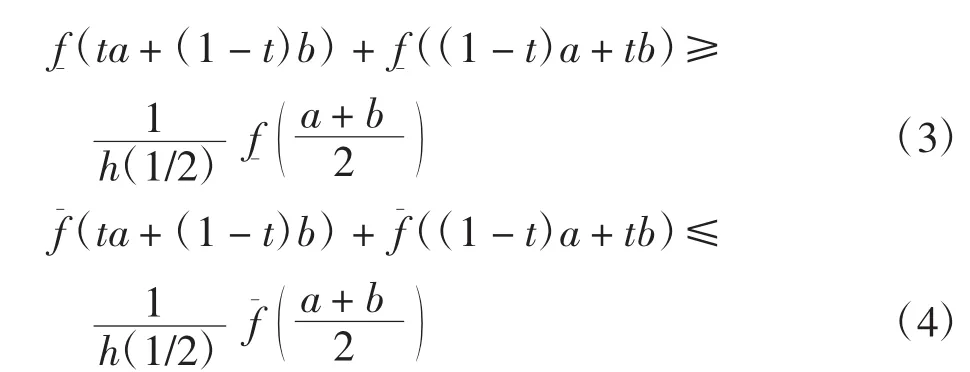
对式(3)和式(4)在[0,1]上关于t积分,则有
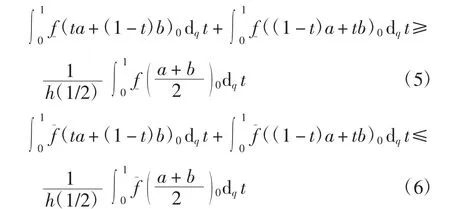
由q-积分的定义可得
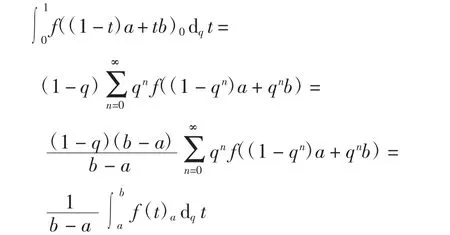
故式(5)和式(6)可改写为
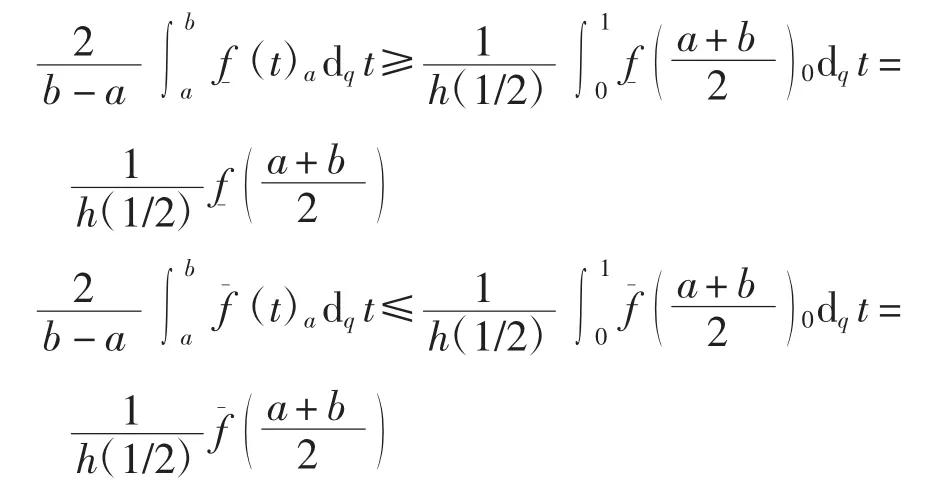
从而有
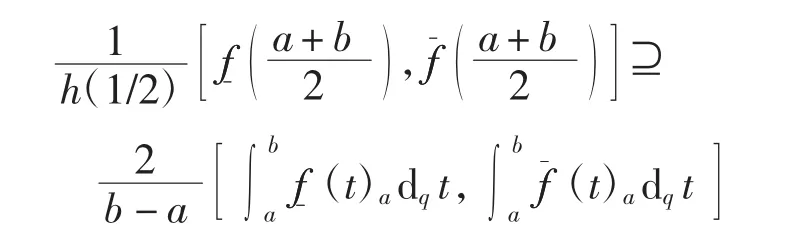
即
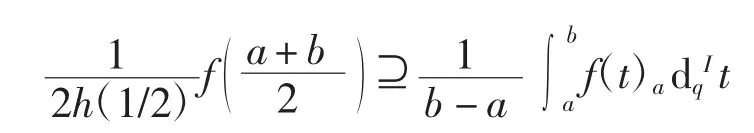
再由区间h-凸函数的定义可得
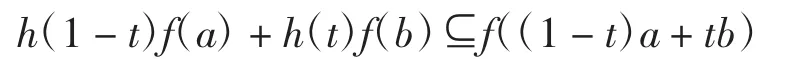
进一步有
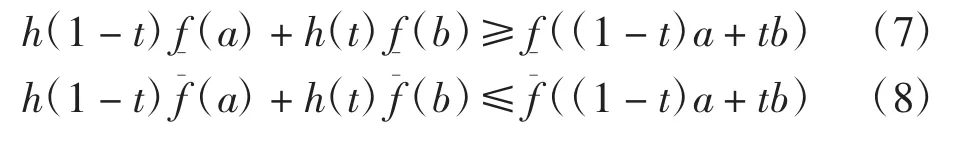
对式(7)和式(8)在[0,1]上关于t积分可得
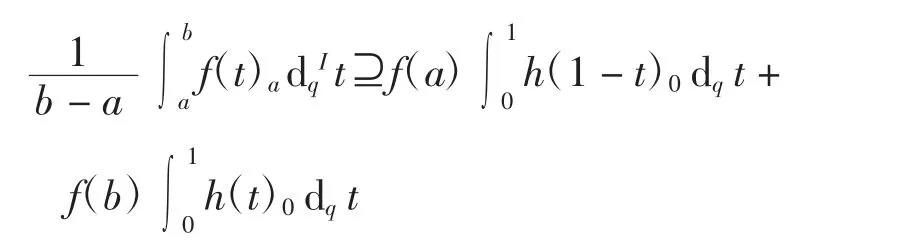
定理得证.
注3当且h(t)=t时,定理 4 退化为文献[7]的定理3.2,即
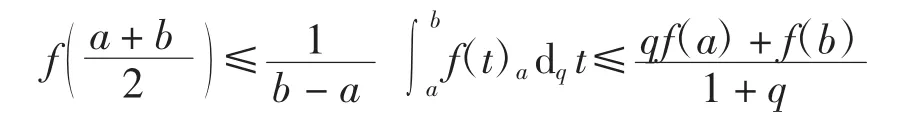
定理5设f、g:J→Kc(R)为2个区间h-凸函数,且[0,1]→R为2个非负函数.若f、g∈SX(h,J,Kc+(R))且f、g∈Iq([a,b]),则有
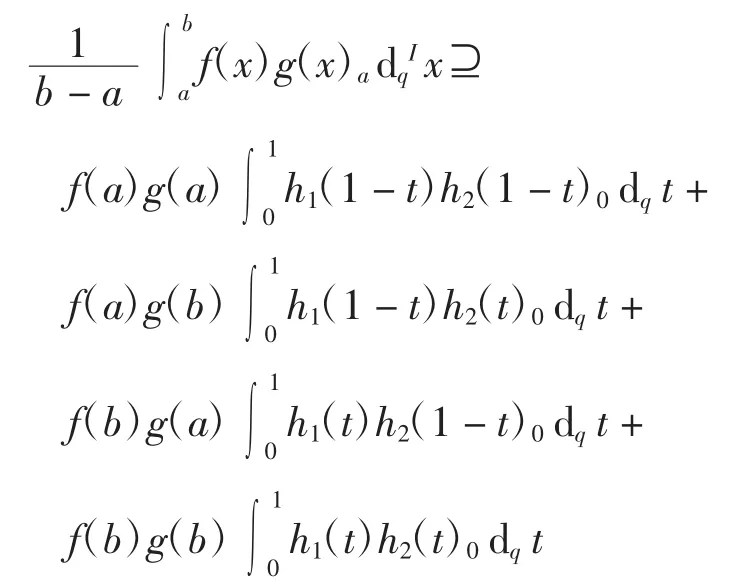
证明由区间h-凸函数的定义得

则有
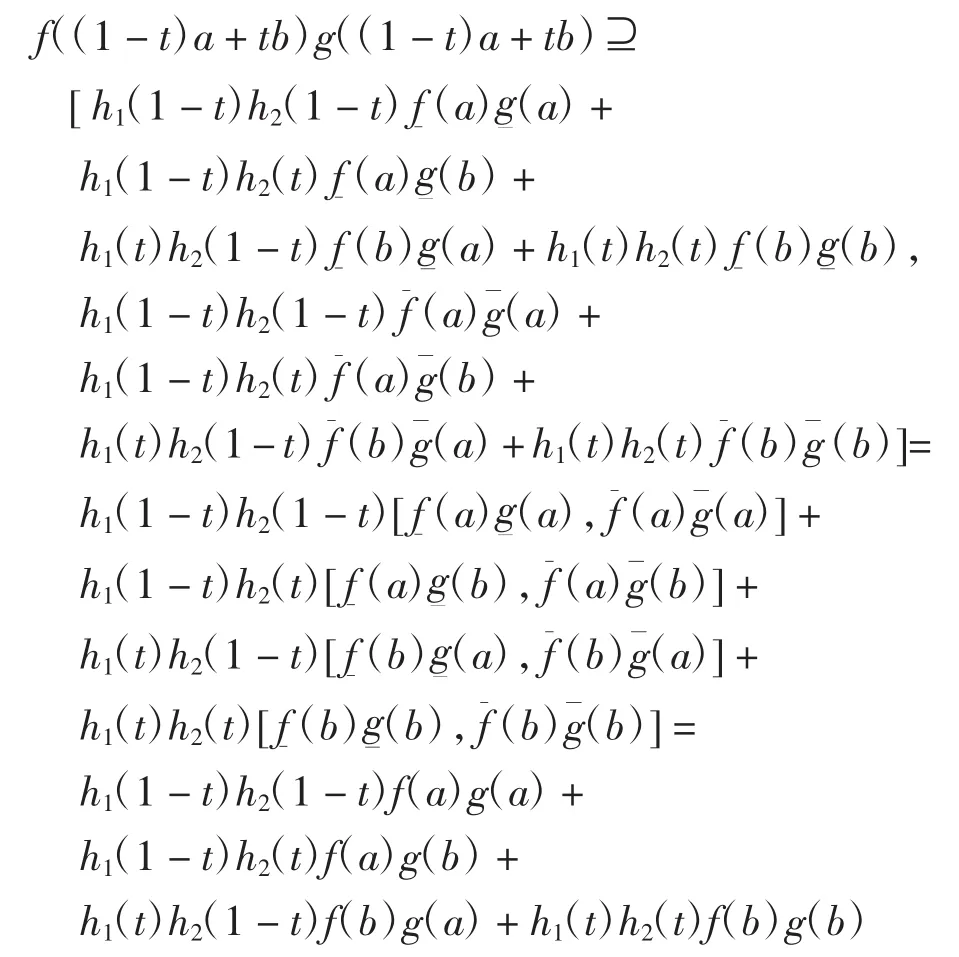
进一步可得
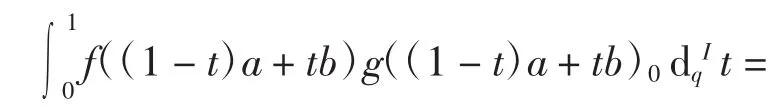
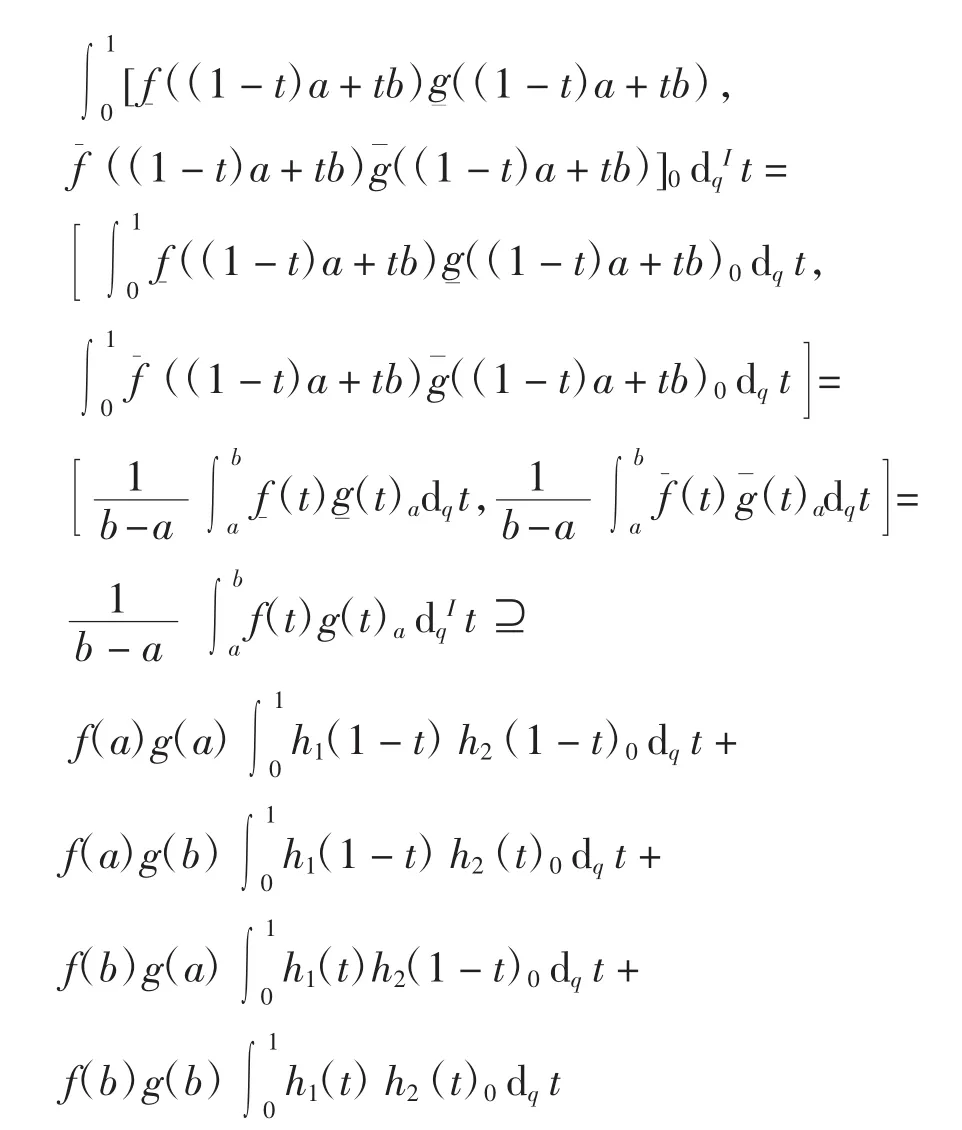
定理得证.
注4当时,定理 5 退化为文献[14]的定理 4.3(i),即
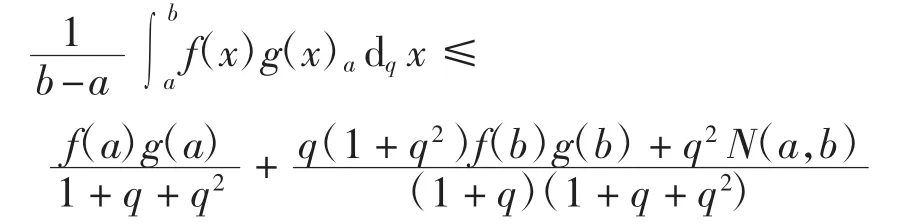
其中N(a,b)=f(a)g(b)+f(b)g(a).
定理6设f、g:J→Kc(R)为2个区间h-凸函数,为2个非负函数,且h1(1/2)h2(1/2)≠0.若f、g∈SX(h,J,Kc+(R))且f、g∈Iq([a,b]),则有
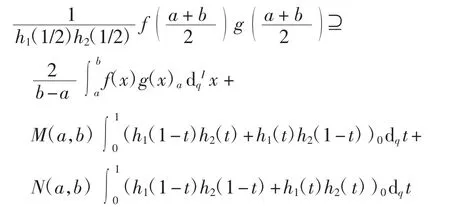
其中:N(a,b)=f(a)g(b)+f(b)g(a),M(a,b)=f(a)·g(a)+f(b)g(b).
证明由区间h-凸函数的定义得
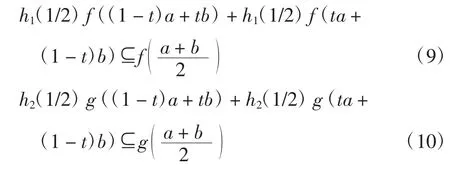
则有

进一步得到
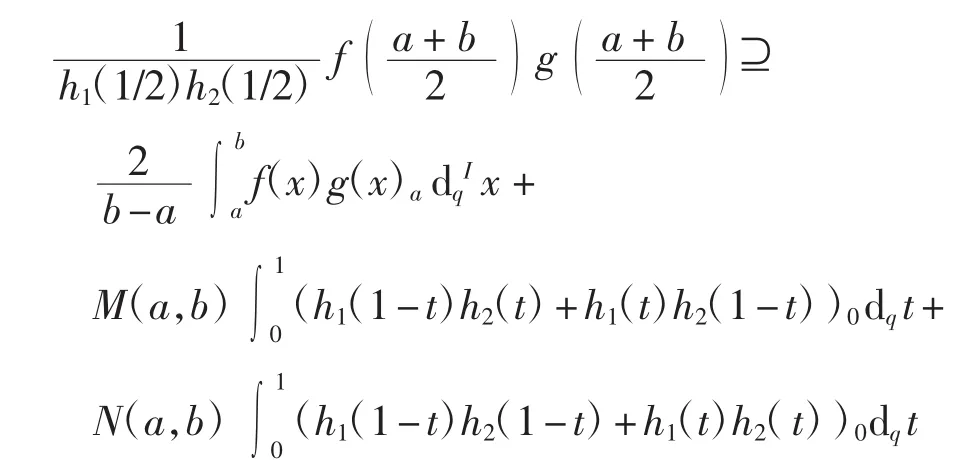
定理得证.
注5当且h(t)=t时,定理 6 退化为文献[14]的定理 4.3(ii),即