桥塔临时附着结构风致抖振响应时域分析

江帆， 吴 超， 张家玮*

(1.91053部队， 北京市 100070； 2.西南交通大学 土木工程学院)

1 概述

随着桥梁结构设计中桥塔高度的不断增加，塔式吊机已成为桥梁高墩、高塔施工中重要的运输起吊设备。在部分桥塔的架设施工中，塔式吊机结构因为无法直接架设在桥塔塔柱上，故而需要设置临时托架，并沿着主塔高度设置附着杆件，此种临时施工结构刚度较小，受脉动风作用时可能发生较大的抖振响应，可能危及施工期间桥梁结构和施工人员的安全。

对于结构的抗风抖振分析涉及大量随机因素影响，因此实际工程问题对其使用的随机分析方法有着较高的计算精度要求。脉动风场可以看作一个平稳随机过程，对于处理平稳随机过程，常用方法有两种：① 基于线性滤波技术的回归方法；② 基于三角级数叠加的谱解法。回归方法的计算速度快，但算法较复杂，总体仿真精度较差，需要估计模型的类型和参数等；谱解法相较于回归方法，计算工作量较大，但算法简单，且理论比较完善，仿真结果比较可靠。不过，随着计算机技术的飞速发展和计算效率的不断提高，谱解法更加适用于现阶段工程应用。目前，国内外大量桥梁结构的风致响应计算常采用谱解法原理进行数值模拟分析，其计算准确性得到大量证实。因此，桥梁结构风致抖振计算经常采用谱分解法的原理来进行数值模拟分析。

在桥梁抗风研究和工程验算中，主要针对施工和运营中的桥梁结构本身，而针对桥塔吊机这一类临时结构的研究相对较少。该类结构刚度较小，容易发生较大晃动影响正常施工，甚至发生安全问题。因此有必要对该种结构进行风致抖振响应研究。该文针对沪通长江大桥桥塔及吊机附着结构，利用谱分解法进行桥址处的脉动风场模拟，研究不同风向角和风速下的桥塔吊机结构的抖振响应，为同类施工设计提供参考。

2 工程背景

2.1 工程概况

以沪通长江大桥为工程实例，该桥全长2 300 m，为公铁两用斜拉桥。采用双塔三索面斜拉桥布置，其中28#、29#主塔高325 m，上塔柱施工布置1台起重力矩为27 000 kN·m的塔式吊机，下文简称塔吊。塔吊标准节段底部设置托架结构，并沿主塔高度设置附着杆件。其中，底部支架结构由钢靴、压杆、支撑框架等组成，压杆钢管内灌注混凝土。附着杆件共5道，每道附着包含4根杆件，均采用相同尺寸工字形截面的Q235钢制作，附着杆一端与附着框销接，另一端与墙体埋件焊接。塔吊结构布置示意图如图1所示。

根据设计桥址处的地形资料，桥位风随高度变化采用指数规律，地表粗糙度系数α=0.12，属A类地表。地表粗糙度高度z0=0.01 m。塔吊工作状态设计风速为13.3 m/s，非工作状态设计风速为39.3 m/s。

2.2 有限元模型

采用有限元软件Ansys建立桥塔与塔吊结构有限元模型，除附着杆件采用Link8桁架单元外，其余均采用Beam44梁单元进行建模。桥塔的两塔柱底部均使用固定约束，约束6个方向自由度，附着杆件和主塔之间采用共节点连接，未释放约束自由度。5道附着阶段的桥塔与塔吊结构有限元模型如图2所示。

图2 5道附着阶段有限元模型图

3 桥塔及塔吊风致抖振计算

3.1 气动力计算

由于桥塔外形沿高度方向变化，为了得到该桥梁的静气动力系数，在不同高度位置选取桥塔模型的典型断面进行数值模拟，采用CFD软件建立流场和结构模型，计算出对应截面的静气动力系数，其他模拟截面的系数按照插值进行计算。

共计算6个不同截面高度处桥塔截面静气动力系数，其中上塔柱截面计算时考虑塔吊标准节段。由于塔吊标准节段为钢桁架结构，利用等效计算的方法，采用二维平面结构等效模拟三维桁架结构，可有效地降低建模难度和提高计算效率。在建模过程中为了确保二维模型气动特性计算的真实性，需保证数值模型桁架结构部分的挡风面积和实际结构相同，且构件断面形状相近。数值计算中考虑到桥塔与塔吊的相对位置关系，将其放入同一流场计算静气动力系数。并与单独桥塔和塔吊结构气动力计算结果进行比较。

采用1∶60比例尺进行CFD建模，整体计算域为矩形，高度和宽度分别为桥塔截面特征长度的25倍和40倍。左边界为速度入口边界，右边界为压力出口边界，上下为对称边界。计算区域采用四边形非结构化网格，并在桥塔截面周围区域进行加密，总网格数约35万个。取桥塔上塔柱中截面及塔吊结构的网格划分如图3所示。

图3 桥塔上塔柱与塔吊截面网格划分图

计算不同风向角与横桥向分别为0°、45°、90°、135°、180°、225°、270°、315°共8个角度下的抖振响应结果。在气动力计算时采用对于角度和位置关系进行建模计算。其中风向角0°的流场划分见图3。

计算方法采用二维数值模拟，流动为定常不可压，静力按定常处理，不考虑温度的影响。对应的数学模型为雷诺时均N-S方程，湍流模型为标准k-ε模型，近壁面以标准壁面函数处理，压力速度耦合选用SIMPLE算法，离散格式为二阶迎风插值。速度入口边界的风速取15 m/s。

以上塔柱截面为例，桥塔截面与塔吊结构的静气动力系数计算结果如表1所示。

由表1可知：在部分风向角下，桥塔结构对塔吊结构造成气动干扰，使塔吊结构阻力系数CD在部分风向角增大，而部分角度明显减弱甚至出现负值。

3.2 脉动风场模拟和荷载的时域化

采用谱分解法原理进行数值模拟分析。为了得到脉动风速时程，针对一个一维n变量、零均值的高斯随机过程，可采用平方根法进行分解该随机过程的谱密度矩阵，并利用快速傅里叶变换方法，最后可得到风速时程。在模拟该桥塔的风速谱时程时依据规范，选用Kaimal-Simiu谱。其水平脉动风谱计算表达式如下：

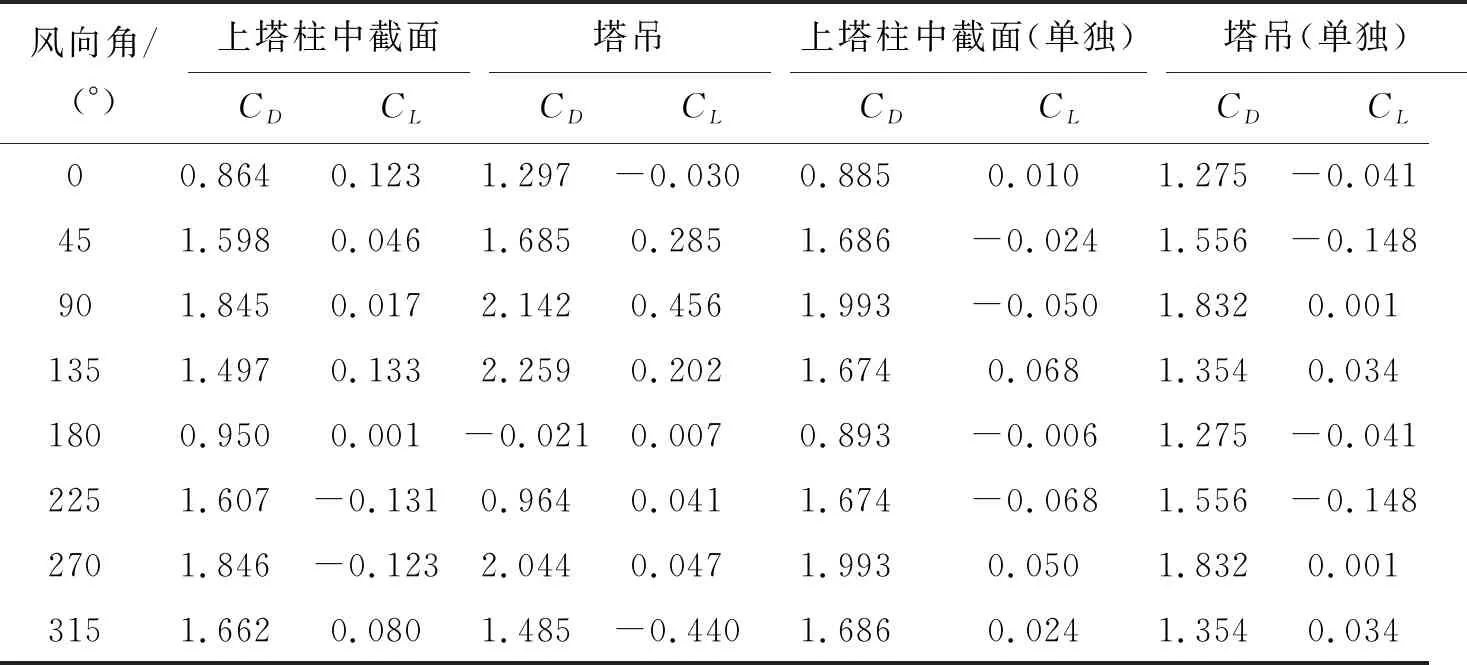
表1 桥塔上塔柱中截面及塔吊静气动力系数

顺风向脉动风谱：

(1)

根据以上方法，通过编程实现从风谱到任意空间位置处的风速时程的模拟。采用此程序进行不同风向角下桥塔和塔吊位置处的风场模拟。风场模拟取截止频率ωu=5π rad/s，频率点个数N=1 024，时间步长Δt=0.1 s。最后模拟得到塔吊工作和非工作状态设计风速下的桥塔上代表位置的脉动风速时程，非工作状态下上塔柱中截面以及塔吊处脉动风速时程如图4、5所示。把通过模拟得出的上塔柱中截面的顺风向脉动风速时程作为检验功率谱，与目标谱进行比较，如图6所示，可以看出该脉动风速模拟满足要求。

图4 非工作状态上塔柱中截面顺向脉动风速时程

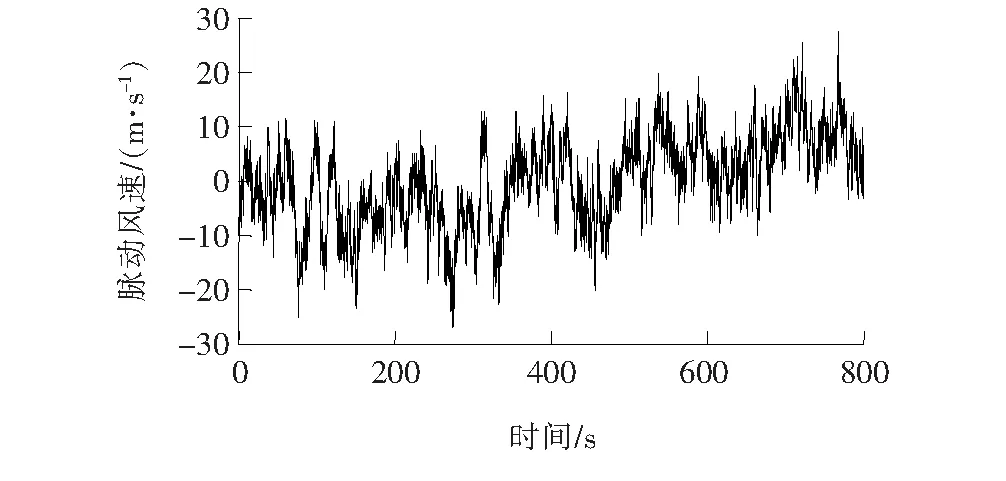
图5 非工作状态塔吊顺向脉动风速时程

图6 上塔柱中截面顺向脉动风速功率谱的检验结果

利用模拟所得的风速时程，不考虑气动导纳的影响，基于准定常假设推导出的Davenport准定常抖振力模型和数值计算所得的结构气动特性，计算得到桥塔和塔吊结构的抖振力时程。在Ansys中，将静风荷载和抖振力时程加载到桥塔和塔吊结构有限元模型上，从而可以进行抖振响应的时域分析。计算时长取为800 s，时间间隔为0.1 s。计算时考虑几何非线性的影响，采用完全法收敛准则进行分析，结构阻尼采用瑞利阻尼。分别计算了桥塔和塔吊整体结构在8种风向角下的抖振响应。

4 塔吊抖振位移响应结果

4.1 5道附着结果

抖振分析主要针对5道附着杆件受力以及塔吊顶部位移，对于塔吊工作状态和非工作状态，0°向角下第5道附着杆件轴力和塔吊顶部位移如图7、8所示。

图7 非工作状态0°风向角第5道附着杆件抖振轴力时程图

将8种风向角工况下塔吊结构的5道附着杆件的抖振内力响应进行统计分析，得到每道附着4道杆件所受到的抖振响应的最大轴向力包络曲线，如图9、10所示。

由图9、10可知：当风向角在90°和270°附近时，即塔吊结构、桥塔连线与来流风向近似垂直时，附着杆件轴向力波动最大；当风向角为0°和180°时，抖振轴力相对较小；在塔吊工作风速和非工作风速下，最大抖振响应均位于第5道附着位置，这是由于第5道附着杆件上方的塔吊结构属于悬臂状态。由于附着杆件均采用相同截面尺寸的Q235钢制作，因此第5道附着杆件为最不利部位。

图8 非工作状态0°风向角塔吊顶部位移时程图

图9 工作状态附着杆件最大抖振轴力包络曲线

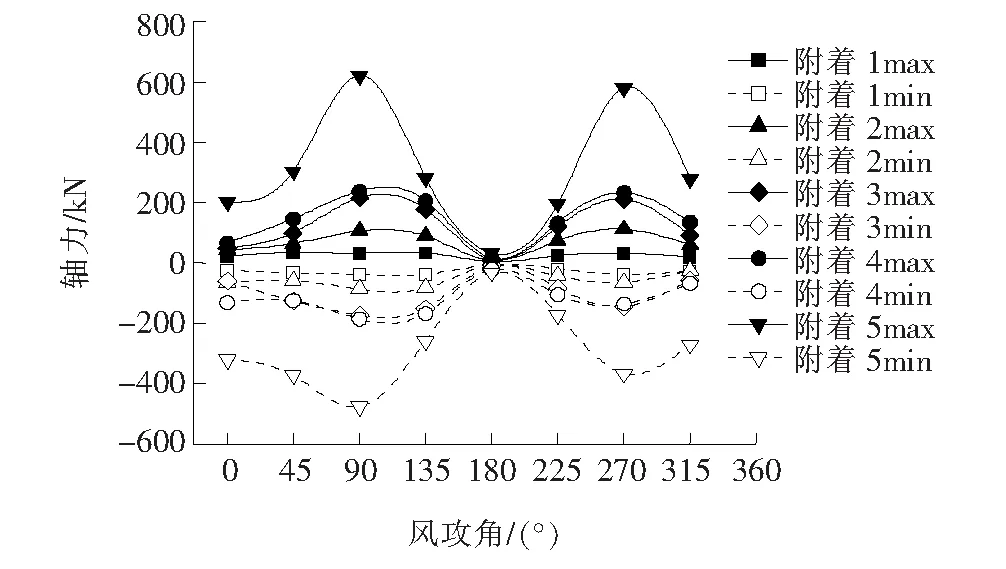
图10 非工作状态附着杆件最大抖振轴力包络曲线

在工作状态和非工作状态风速下的8个风向角，塔吊底部框架和钢靴反力以及塔吊抖振位移结果如表2、3所示。

由表2、3可知：在工作状态风速下，抖振响应对附着杆件反力、框架底部及钢靴支点反力、框架和钢靴的纵横桥向剪力及塔吊顶部的抖振位移的影响不大，抖振响应引起的附着杆件的轴力最大为47.4 kN，框架反力和钢靴反力最大为7.1 kN。在非工作状态风速下，抖振响应引起的附着杆件的轴力最大为620.7 kN，框架反力和钢靴反力最大为96.2 kN。由结果可知，5道杆件附着状态，工作风速和非工作风速下的抖振响应较小，抖振响应均偏于安全。

表2 工作状态风速5道附着杆件及支点抖振响应结果

表3 非工作状态风速5道附着杆件及支点抖振响应结果

4.2 4道附着结果

由受力结果可知，最上层附着杆件上端的塔吊结构处于悬臂状态，使最上层的第5道附着杆件受到最大的抖振作用力，因此有必要计算第5道附着杆件未连接时，塔吊处于4道附着时的抖振内力，结果如表4所示。

表4 非工作状态风速4道附着杆件及支点抖振响应结果

在非工作状态下，4道附着时的抖振响应影响较大，抖振响应可使得附着杆件的轴力最大为-1 074.6 kN，框架反力和钢靴反力最大为83.6 kN，框架和钢靴纵支点横桥向剪力最大为14.9 kN，最大抖振位移可达309.3 mm。由此可知，非工作状态风速下，附着杆件轴力在规定范围以内，但引起塔吊结构较大的位移，不利于施工安全。

5 结论

通过对沪通长江大桥桥塔和塔吊附着结构8种风向角进行脉动风响应分析，得出以下主要结论：

(1) 在工作状态下，脉动风速相对较小，对附着杆件的抖振轴力、钢框架支座反力和剪力以及塔吊顶部的抖振位移的影响均较小，可以忽略该脉动风的动力响应。

(2) 在非工作状态下，脉动风速相对较大，对附着杆件的抖振轴力影响较大，而对于钢框架支座反力和剪力以及塔吊顶部的抖振位移的影响相对较小，因此应考虑脉动风对附着杆件的抖振轴力响应的影响。

(3) 由于最上层附着杆件上方的塔吊结构属于悬臂状态，最上层附着杆件所受抖振作用力最大，且与静力荷载作用下受力最大的杆件一致。所以对塔吊抬升过程中4道附着状态和5道附着状态均进行了抖振响应分析。

(4) 在4道附着状态的非工作状态风速下，抖振计算结果可知，抖振响应可使得附着杆件的轴力最大，可达-1 074.6 kN，最大抖振位移可达309.3 mm。因位移过大不利于施工安全。