大跨度钢筋混凝土拱桥施工阶段动力特性分析

韩洪举， 张基进

(贵州路桥集团有限公司， 贵州 贵阳 550001)

桥梁结构的动力特性包括固有振型序列及相应自振频率，是研究桥梁抗震性能、抗风稳定性能等动力问题的基础。针对施工阶段最大单悬臂状态下的钢筋混凝土箱形拱桥进行动力特性研究，对于评估拱桥在施工阶段中的抗震、抗风性能具有重要意义。

宗周红等对某座钢筋混凝土箱形拱桥进行了全桥现场环境振动试验，并识别得到了桥梁的各方向振动特性，然后通过与Ansys三维有限元模态分析结果相比对，表明试验与理论分析具有良好的吻合性，阐述了对钢筋混凝土箱形拱桥进行有限元动力特性分析的有效性；刘伯栋等利用有限元通用软件Ansys对一座中承式钢筋混凝土拱桥进行了动力特性的数值模拟分析，研究了矢跨比、横撑布置、拱肋刚度等因素对这类拱桥动力特性的影响；程怀江分析了影响中承式钢筋混凝土拱桥动力特性的敏感性因素，并研究了过桥车辆等活荷载对拱桥的动力响应。这些研究均为针对成桥状态的钢筋混凝土拱桥，而对施工阶段的大跨度钢筋混凝土拱桥的动力特性研究未见报道。

该文以某上承式钢筋混凝土箱形拱桥为例，利用大型通用有限元软件Ansys分析了该种桥型的动力特性，分析中考虑了拱圈、拉索与扣塔的耦合效应，研究了扣塔刚度及扣锚索索力等施工阶段重要结构参数对大跨度钢筋混凝土箱形拱桥动力特性的影响，研究成果可为大跨度钢筋混凝土箱形拱桥施工阶段抗震、抗风性能研究提供技术支持。

1 工程概况

某大跨度拱桥为主跨240 m的上承式钢筋混凝土空腹箱形拱桥，拱轴系数为1.85，净矢高为40 m，净矢跨比为1/6。主拱圈采用等高截面悬链线拱，拱圈截面为单箱双室，箱宽10 m，箱高4.5 m。根据顶底板厚度及腹板厚度变化，拱肋沿径向可分为5种截面。该桥总体布置如图1所示。

图1 主桥总体布置图(单位：cm)

主拱圈采用斜拉扣挂法悬臂浇筑施工完成，该法通常首先在拱脚墩、台顶部安装临时格构塔架，并在扣塔两侧对称安装扣索和锚索，再通过以扣索为支点的挂篮悬臂浇筑节段混凝土拱箱。通过调节扣索索力，可以对悬臂拱肋的线形和受力状态进行调整，从而使悬臂拱圈保持平衡。

2 有限元计算方法

该文采用大型通用有限元软件Ansys对该桥进行施工阶段动力特性分析，在建立有限元模型时，主要考虑主拱圈、扣锚索和扣塔之间的耦合效应。Ansys提供了多种数值方法来计算结构的动力特性，包括分块Lanczos法、子空间迭代法、Power Dynamics法、缩减法、非对称法、阻尼法和QR阻尼法。对于复杂的大型结构而言，其结构响应主要由前10阶振型所控制。考虑到较容易确定桥梁结构低阶振型频率范围，该文采用计算精度高、速度快的分块Lanczos法进行模态分析。

3 分析模型

采用大型有限元通用软件Ansys建立一体化三维有限元模型。在有限元建模时，主拱圈和扣塔均采用三维梁单元(Beam188)模拟，并采用实际设计截面进行建模，以尽量精确地考虑结构刚度的分布。考虑到扣塔建立在边墩顶部，分别对钢扣塔和混凝土边墩建模，并将两者用刚臂连接，刚臂单元采用Beam4单元模拟；扣锚索采用只受拉的空间杆单元(Link10)模拟，每条扣锚索都模拟成一个单元，并通过计入初应变来施加初始索力。拱圈、扣塔和扣锚索均依据初步设计图纸所提供的混凝土和钢材实际用量计算平均密度值，并通过设置单元密度来施加结构质量，以考虑其质量对结构动力特性的影响，保证模态分析的正确性。对于该分析模型的边界条件处理为：拱顶自由，不施加约束；拱脚施加固结约束；扣塔底部与边墩顶部使用刚臂连接，边墩底部施加固结约束；锚索锚固点施加固结约束。有限元模型共包含1 175个节点和1 397个单元。

4 动力特性分析

采用分块Lanczos法对该桥三维有限元模型进行模态分析，并提取结构前10阶振型和自振频率。最大单悬臂状态下，该模型的前10阶振型描述及相应自振频率见表1。

表1 大桥主桥施工阶段最大单悬臂状态前10阶自振频率和振型特征

从表1及振型图可以看出：考虑扣塔、拉索、拱圈间的耦合作用，施工阶段最大单悬臂状态下的大跨度钢筋混凝土箱拱桥的振型比较复杂，具有以下特点：

(1) 结构的典型振型包括拱圈侧弯、竖弯、扭转，扣塔侧弯、扭转等模态，后面的振型较为复杂，出现了拱圈与扣塔之间相互耦合的振型。

(2) 拱圈横向振动先于竖向振动出现。这表明大跨度钢筋混凝土拱桥在施工阶段最大单悬臂状态下，拱圈面外刚度小于面内刚度，面外的稳定性问题相对于面内更为突出。

(3) 结构的扣塔横向振动出现在拱圈横向振动之后，表明扣塔的横向刚度大于施工状态下的拱圈横向刚度。

5 参数分析

5.1 扣塔刚度

为了分析扣塔刚度对施工阶段最大单悬臂状态拱圈自振频率的影响，在原三维有限元模型的基础上，改变扣塔的刚度，缩放比例为0.8倍和1.2倍，分别考虑扣塔刚度的放大和缩小。不同工况下典型振型自振频率相对于原模型计算结果的频率变化率如图2所示。

由图2可知：结构各阶振型的自振频率随扣塔刚度变化的趋势相同，都随刚度增大而有不同程度的提高；扣塔刚度变化对拱圈竖弯频率与侧弯频率影响较小；而减小扣塔刚度对拱圈扭转频率影响较大。

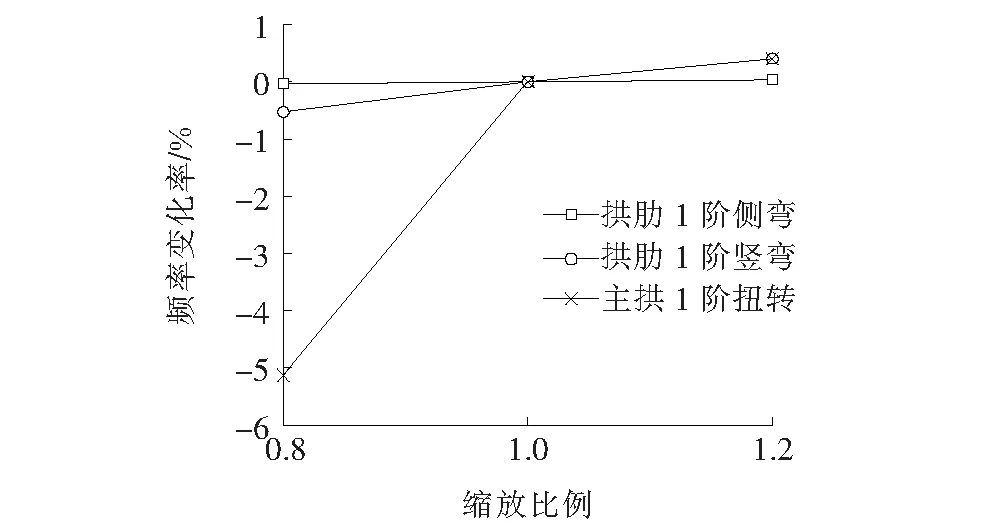
图2 扣塔刚度对结构自振频率的影响

5.2 扣锚索索力

为了分析扣锚索的索力对该桥施工阶段最大单悬臂状态结构动力特性的影响，在三维有限元模型中考虑4种计算工况：工况1为1.2倍扣索索力；工况2为1.2倍锚索索力；工况3为同时将扣、锚索索力放大1.2倍；工况4为同时将扣、锚索索力放大1.5倍。改变扣锚索索力后，结构自振频率与原模型自振频率对比见表2。

从表2可以看出：扣锚索索力对施工阶段最大单悬臂状态下钢筋混凝土箱形拱圈自振频率影响较小；不同工况下拱圈侧弯、竖弯及扭转振型的自振频率均随扣锚索索力增加而有所降低。

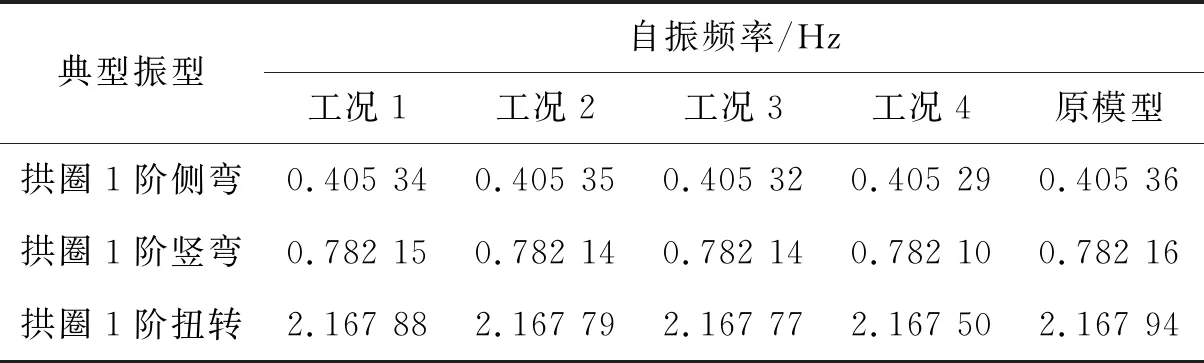
表2 扣锚索索力对桥梁自振频率的影响

6 结论

(1) 斜拉扣挂法悬臂浇筑施工的钢筋混凝土箱形拱桥在最大单悬臂状态下的典型振型包括拱圈侧弯、竖弯及扭转和扣塔侧弯等模态。由于扣塔与拱圈之间的耦合效应，对拱桥施工阶段的动力特性分析，应该建立拉索、扣塔、拱圈一体化模型，以获得更精确的计算结果。

(2) 扣塔刚度变化对拱圈侧弯和竖弯频率影响较小，减小扣塔刚度对最大单悬臂状态下的拱圈扭转频率影响较大，因此在拱圈施工阶段抗风稳定性计算中应适当考虑这方面影响。

(3) 扣锚索索力变化对最大单悬臂状态下的拱圈动力特性影响较小，考虑到索力主要由悬臂状态下拱圈结构内力、线形所确定，因此不宜通过调整索力来改变结构动力特性。