钢筋混凝土拱桥参数敏感性分析

谭亚杰

（长沙理工大学土木工程学院 长沙 410114）

某特大桥是一座采用扣锚索悬臂扣挂法施工的钢筋混凝土拱桥，是一种由塔、索、拱肋3 种基本结构组成的组合结构。本文依托某特大桥为背景，运用有限元软件Midas∕Civil对施工过程中涉及的各参数进行敏感性分析，确定悬臂扣挂施工过程中的敏感性参数，为类似桥梁施工误差提供参考。

1 工程概况

某特大桥位于湖南省湘西自治州永顺县，主孔为净跨径195 m 的RC无铰箱型拱，矢跨比1∕5，拱轴线为悬链线，拱轴系数m=1.543，主拱圈尺寸为360 cm（高）×780 cm（宽）。扣锚索均采用φ15.2 mm 的低松弛预应力钢绞线，共42 对扣锚索，该特大桥施工布置如图1所示。

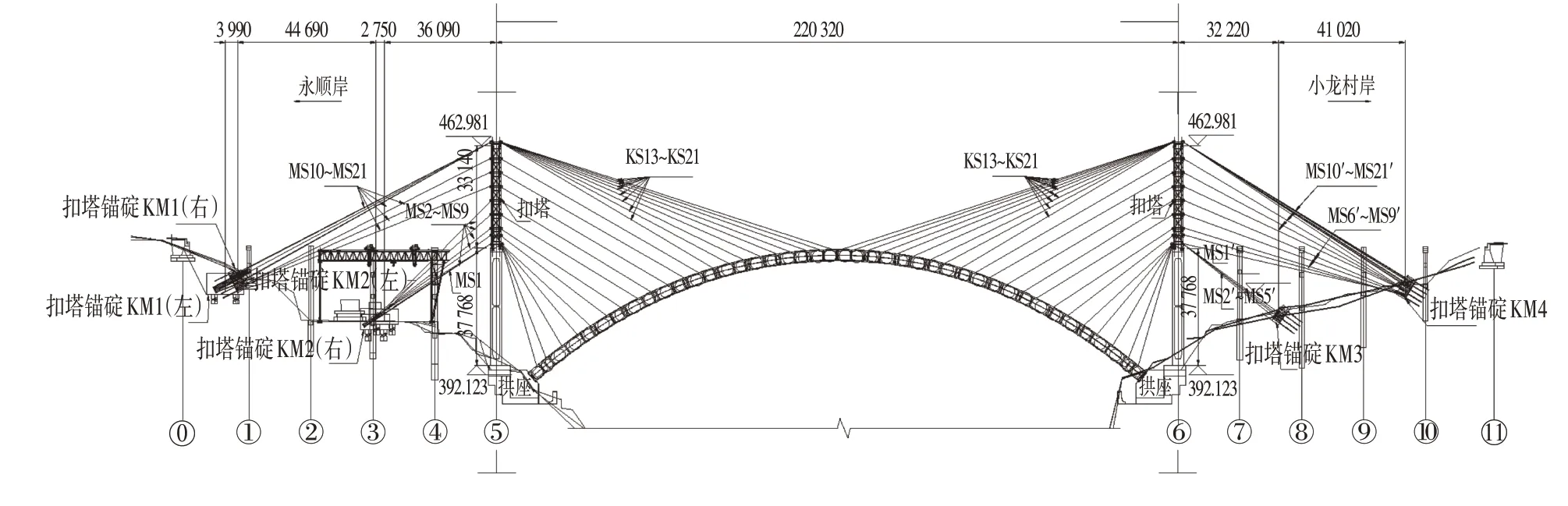
图1 某特大桥施工布置Fig.1 Construction Layout of a Super Major Bridge（mm）

2 建立有限元模型

采用有限元软件MIDAS∕Civil 建立某特大桥模型，使用桁架单元模拟扣锚索，其余构件采用梁单元模拟。地锚索锚固处和交界墩与基础采用完全固结、主拱圈和拱上立柱、临时扣塔和交界墩的连接采用刚性连接，拱上立柱和主梁的连接采用弹性连接里的刚性连接。根据设计图纸，共划分为74 个施工阶段，如表1所示，有限元模型如图2所示。

表1 施工阶段的划分Tab.1 Division of Construction Phase

图2 某特大桥有限元模型Fig.2 Finite Element Model of a Super Major Bridge

3 参数的选取

在施工过程中由于影响结构力学性能的因素众多，如混凝土的欠、超浇注和模板变形等［1］，导致主拱圈自重产生偏差；在实际拱段浇注中，混凝土的弹性模量与设计值有些偏差［2］，以及模板误差，直接导致主拱圈刚度的误差，本文仅考虑主拱圈弹性模量引起的偏差；由于测量、温度变化、张拉技术的限制以及应力松弛等原因［3］。使扣锚索张拉时索力不能准确达到预定值，引起扣锚索索力偏差；由于扣锚索的制作误差［4］。引起扣锚索刚度偏差，这里仅考虑扣锚索弹性模量的偏差。

为了保证主拱圈在施工过程中满足变形和应力的要求，本文选取主拱圈自重、主拱圈刚度、扣锚索索力、扣锚索刚度等参数进行分析。在模型分析时，以基准状态为设计状态，分别改变某一参数，同时保持其他参数不变，进行有限元分析计算［5］。计算到成桥状态下主拱圈的累计位移以及累计应力的变化量，根据各设计参数影响程度确定敏感性参数和不敏感性参数［6］。根据现场施工实际情况和相关文献［7-9］，确定各参数变化程度如表2所示。

表2 结构主要参数及其变化Tab.2 Main Structural Parameters and Their Changes

4 参数敏感性分析

4.1 主拱圈变形分析

按表2 结构参数的变化，逐一改变模型中主拱圈自重、主拱圈刚度、扣锚索索力、扣锚索刚度等参数值，对施工全过程进行参数敏感性分析，计算到成桥状态下主拱圈累计竖向位移差，结果如图3所示。

图3 参数变化时主拱圈累计竖向位移差Fig.3 Cumulative Vertical Displacement Difference of Main Arch Ring when Parameters Change

由图3 可知，各设计参数对主拱线性的影响呈对称分布。从拱脚至拱顶处位移差先增大后减小。当主拱圈自重增大5%时，主拱圈向下挠度增大，并且在11#拱段处达到最大值，竖向位移最大差值为31.69 mm，位移变化幅度高达264%，属于位移敏感性参数。当主拱圈刚度增大5%时，主拱圈位移受主拱圈刚度的影响很小，最大变化量仅有2.18 mm，属于位移不敏感性参数。当扣锚索索力增大5%时，由于索力的增大，主拱圈从竖直向下位移变为竖直向上位移，在11#拱段达到最大值，竖向位移最大差值为34.34 mm，变化幅度最大，为286%，为位移敏感性参数。当扣锚索刚度增大5%时，对主拱圈线性的影响较小，仅有1.63 mm。属于位移不敏感参数。

4.2 主拱圈应力分析

在施工全过程中，主拱圈的应力控制十分重要，各参数引起的拱圈上下缘累计应力变化值如图4所示。

由图4 可知，主拱圈自重、扣锚索索力增大时，对上下缘应力的影响有着相同的规律，在3#拱段处上下缘累计应力变化差值最大，拱顶处变化差值最小，主拱圈自重增大5%时，3#拱段处最大累计应力差值是1.74 MPa，扣锚索索力增大5%时，3#拱段处最大累计应力差值是1.53 MPa。而对于主拱圈刚度和扣锚索刚度对主拱圈应力几乎无影响，最大差值仅为0.021 MPa、0.019 MPa。主拱圈自重和扣锚索索力为应力敏感性参数，主拱圈刚度扣锚索刚度为应力不敏感性参数。

图4 参数变化时主拱圈上下缘应力累计应力差Fig.4 Cumulative Stress Difference of Upper Edge Stress of Main Arch Ring when Parameters Change

对上述4个设计参数对主拱圈结构响应情况进行汇总，如表3所示。

表3 影响参数变化下主拱圈位移和应力变化最大值Tab.3 Maximum Value of Displacement and Stress Change of Main Arch Ring under Change of Influencing Parameters

5 结论

通过MIDAS∕Civil 软件对某特大桥进行施工阶段的参数敏感性分析，得到各参数对主拱圈线性和应力的影响程度以及施工过程中的变化规律：

⑴从各设计参数对主拱圈位移和应力的响应来看，主拱圈自重和扣锚索索力为敏感性参数，在桥梁施工监控过程中，加强对主拱圈自重和扣锚索索力监测。主拱圈刚度和扣锚索刚度为不敏感参数，基本可以忽略这两种参数的影响。

⑵主拱圈自重和扣锚索索力变化时，对主拱圈1∕4L处的位移响应影响最大，对3#拱段处应力响应影响最大，应在施工过程中严格控制主拱圈1∕4L处位移和3#拱段的应力要求。

⑶在施工过程中对结构位移和应力影响较大的参数进行严格的控制和监测，比如在主拱圈拱段制作过程中严格控制混凝土的用量、模板尺寸误差、索力测量误差、张拉误差等［10］，以及根据具体情况对主拱圈自重和扣锚索索力进行及时的修正，以保证主拱圈截面在施工过程中满足变形和应力的要求。