例谈数列中的奇偶项问题

◇ 李文东

数列的奇偶项是指数列中的奇数项与偶数项，高考和模拟题中经常出现按奇偶项分类求和的数列问题，这类题目对大部分学生来说难度较大，究其原因，主要是学生解题时缺乏思路.本文针对这一问题进行归纳总结，希望帮助同学们找到解题思路，以快速解决此类问题.

1 奇偶项数列的等差等比数列的证明

本题是按等比数列的定义来证明，证明过程中要注意下标的变化和适用范围.

例2(2014年全国卷Ⅰ理17)已知数列{an}的前n项和为Sn，a1＝1，an≠0，anan＋1＝λSn－1，其中λ为常数.

(1)证明：an＋2－an＝λ；

(2)是否存在λ，使得{an}为等差数列，并说明理由.

(1)由题设anan＋1＝λSn－1，得an＋1an＋2＝λSn＋1－1，两式相减，得an＋1(an＋2－an)＝λan＋1，由于an≠0，所以an＋2－an＝λ.

(2)由题设a1＝1，a1a2＝λS1－1，可得a2＝λ－1，由(1)知a3＝λ＋1.

假设{an}为等差数列，则a1，a2，a3成等差数列，所以a1＋a3＝2a2，解得λ＝4.

下面证明λ＝4时，{an}为等差数列.由an＋2－an＝4知，数列奇数项构成的数列{a2m－1}是首项为1、公差为4的等差数列，即a2m－1＝4m－3，令n＝2m－1，则m＝，所以an＝2n－1(n为奇数).

数列偶数项构成的数列{a2m}是首项为3、公差为4的等差数列，即a2m＝4m－1，令n＝2m，则所以an＝2n－1(n为偶数)，所以an＝2n－1(n∈N∗)，an＋1－an＝2.

因此，存在λ＝4，使得{an}为等差数列.

由an＋2－an＝λ，知数列{an}的奇数项和偶数项分别构成一个公差为λ的等差数列，从而可以分别求出奇数项和偶数项的通项公式，然后再证明{an}为等差数列.

2 奇偶项数列的前n项和

类型1an＋1＋an＝f(n)，于是an＋1＋an＋2＝f(n＋1)，从而an＋2－an＝f(n＋1)－f(n).特别地，若f(n)＝an＋b(a，b为常数)，则an＋2－an＝a，即数列{an}的奇数项和偶数项分别构成一个公差为a的等差数列.

例3已知数列{an}满足an＋1＋an＝4n－3(n∈N∗).

(1)若数列{an}是等差数列，求a1的值；

(2)当a1＝2时，求数列{an}的前n项和Sn.

(1)若数列{an}是等差数列，则

由an＋1＋an＝4n－3，得

两式相减，得an＋2－an＝4，由a2＋a1＝1，a1＝2，得a2＝－1，所以数列{a2n－1}是首项为a1＝2、公差为4的等差数列，数列{a2n}是首项为a2＝－1、公差为4的等差数列，所以

当n为奇数时，an＝2n，an－1＝2n－7.

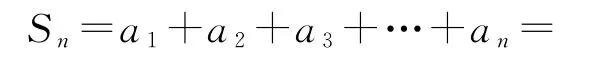
本例中由于数列{an}的奇数项和偶数项分别构成等差数列，其通项公式可分别求出，因此方法1对n分奇偶项讨论并且每一种情况按奇数项和偶数项组合进行求和；方法2基于an＋1＋an＝4n－3的一个整体运用，将相邻两项组合后首先求得数列{an}的前2n项的和，进而得到n为偶数时的Sn，而当n为奇数时，利用Sn＝Sn＋1－an＋1来求.当然这里还是需要知道an＋1，这两种方法是求解奇偶项数列前n项和的两个基本策略.数列中的奇数项、偶数项的问题实质上是将一个数列分成两个新的数列进行考查，易搞错的是新数列与原数列的项数、公差、公比的判定.

例4已知数列{an}中，a1＝1，a2n＝n－an，a2n＋1＝an＋1，数列{an}的前n项和为Sn，求S100.

由题意a2n＋a2n＋1＝n＋1，于是

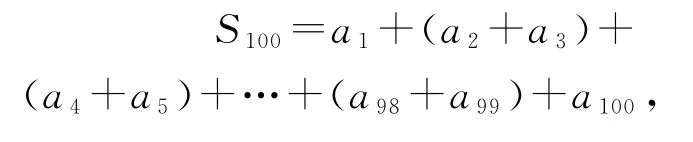
我们只需要求出a100即可，由于a2n＝n－an，a2n＋1＝an＋1，故a100＝50－a50，a50＝25－a25，a25＝a12＋1，a12＝6－a6，a6＝3－a3，a3＝a1＋1＝2，得a100＝31，从而

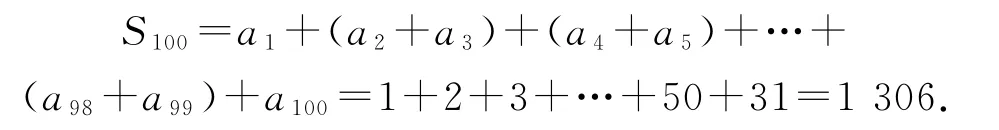
本题采用邻项结合、整体求解，关键是求出a100，这根据条件一步步倒推容易得出.

①中小型第三方物流企业，根据中国物流与采购联合会和全国物流标准化技术委员会协助制定的《物流企业分类与评估指标》，认为中小物流企业的内涵所谓中小型物流企业，是根据企业固定资产年营业额、年上缴利税和企业员工规模划分的一类企业形态[5]。当前一般指那些固定资产1000万元以下、年营业额数百万至数千万、企业员工500人以下的为中小型物流企业。多数为单向型物流企业，它仅仅承担和完成某一项或少数几项物流功能[6]。

类型2an＋1·an＝f(n)，于是an＋1·an＋2＝f(n＋1)，从而.特别地，若f(n)＝a·qn(a，q为非零常数)，则＝q，即数列{an}的奇数项和偶数项分别构成一个公比为q的等比数列.

例5已知数列{an}中

(1)求证：数列{a2n}与{a2n－1}都是等比数列；

(2)求数列{an}的前n项和Sn.

类型3an＋1＋(－1)nan＝f(n)，于是当n为奇数时，an＋1－an＝f(n)，n为偶数时，an＋1＋an＝f(n)；从而当n为奇数时，n＋1为偶数，故

于是

当n为偶数时，n＋1为奇数，故

于是

特别地，若f(n)＝an＋b(a，b为常数)，则

bn＝a4n－3＋a4n－2＋a4n－1＋a4n＝f(4n－2)－f(4n－3)＋f(4n－1)＋f(4n－2)＝8an＋2b－2a，可见数列{bn}是一个首项为6a＋2b、公差为8a的等差数列.

例6(2012年全国卷Ⅰ理16)已知数列{an}满足an＋1＋(－1)nan＝2n－1，则{an}的前60项和为______.

方法1由题意得f(n)＝2n－1，于是当n为奇数时an＋2＋an＝f(n＋1)－f(n)＝2，当n为偶数时an＋2＋an＝f(n＋1)＋f(n)＝4n.故

方法2bn＝a4n－3＋a4n－2＋a4n－1＋a4n是一个首项为10，公差为16的等差数列，于是

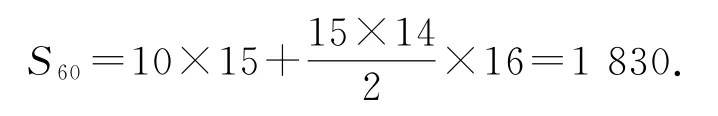
由题目分析知当n为奇数时，an＋2＋an＝an＋2＋an＋4＝2，从而an＋4＝an，若a1＝1，则a4n－3＝1，又a4n－3＋a4n－1＝2，故a4n－1＝1，于是当n为奇数时an＝1，an＋1－an＝2n－1，于是当n为偶数时an＝2n－2，即本题是一道填空题，故假设a1＝1也不失为一种有效的办法.

3 通项含有(－1)n的数列的单调性问题

例7已知数列{an}(n∈N∗)满足a1＝1－3k，an＝4n－1－3an－1(n≥2，k∈R).

(1)求数列{an}的通项公式；

(2)若数列{an}为递增数列，求k的取值范围.

数列的单调性问题，本质上是an＋1－an＞0(或an＋1－an＜0)的不等式恒成立问题，数列{an}的通项公式中含(－1)n，就需对n进行奇偶性讨论，确定(－1)n的值再分离变量转化为数列最值问题.