基于推广ARCH模型的沪深300指数对数收益率波动性研究

任佳顺，胡学平

（安庆师范大学数理学院，安徽安庆246133）

我国股票市场于1990年成立，由于股票市场的监管体制不够完善，我国股票市场波动性较为强烈。为了探究与解决这类问题，越来越多的学者开始把注意力集中在股票市场波动性的研究上。然而，金融数据常常伴随着方差随时间变化而变化，表现为方差集群效应，一般的检验方法很难发现。这类金融时间序列在整个序列观察期，序列的方差基本是齐性的，但是在个别的时间段里方差明显不同于期望方差，这种波动使得一般的ARIMA模型很难取得较好的效果。为解决这一问题，Engle提出利用自回归条件异方差（ARCH）模型来解决异方差问题[1]。但是ARCH模型只适用于异方差短期自相关，而实际中，多数残差序列都具有长期相关性。因此，Bollerslev对自回归条件异方差模型进行了改进，提出了广义自回归条件异方差（GARCH）模型，该模型弥补了ARCH 模型不能有效拟合长期相关的异方差函数的缺点[2]。王皓利用DCC-GARCH 模型对日本股票市场与国际市场波动溢出效应相关性进行了研究与分析，发现日本股指与其他股指之间的正相关性逐步增强，金融危机的发生使得各国股票市场之间的相关性显著提升，而中国的股票市场虽然刚发展不久，但是在世界股票市场中的影响力越来越大[3]。赵婕伶利用GARCH模型对股票市场波动进行了研究，研究表明，使用蒙特卡洛法容易造成对期权价值的低估，从而造成股票的理论价值偏低于实际价值[4]。使用B-S模型估算的期权价值比蒙特卡洛方法高，造成股票的理论价值偏高于实际价值，从而导致债券价值高估[4]。GARCH模型可以很好地拟合具有集群效应的金融数据，使得预测金融的走势变得简单有效。EGARCH模型作为GARCH模型的衍生模型，它侧重于研究金融数据是否具有杠杆效应，可以进一步分析金融市场内部波动的特性，帮助研究员找出导致金融市场波动的原因，针对金融数据不同的走势提出合理的对策建议。

沪深300指数作为我国股票市场的代表，以它作为实证分析对象，能够反映我国股票市场的主要概貌和运行状况。本文通过分析2002年1月至2019年8月近17年来股票市场的收益率状况，运用单变量GARCH模型对收益率的波动性进行探究和刻画，在R软件的辅助下将收益率的波动性可视化，充分把握住股票市场的特点，再结合EGARCH模型，研究对数收益率的波动性是否具有杠杆效应。

1 单变量GARCH模型与指数GARCH模型

GARCH模型结构如下[5]：

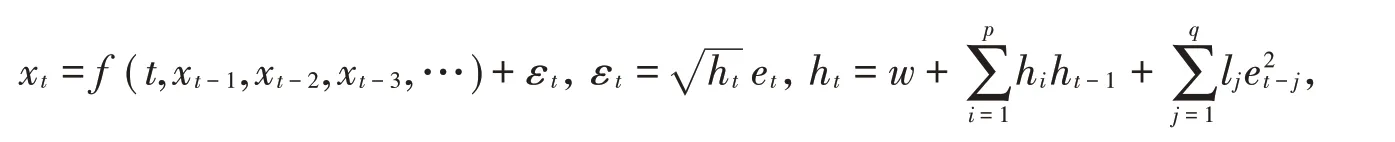
其中f (t,xt-1,xt-2,xt-3,…)+εt为{xt}的确定性信息拟合模型，et服从均值为零、方差为σ2的独立随机序列。

令rt为沪深300指数在t 时刻的对数收益率（rt=log pt-log pt-1，pt为当天的收盘价格，pt-1为前一天的收盘价格），假设给定t-1 时刻的已知信息集Ft-1时的条件均值μt=E(rt| Ft-1)和条件方差ht=Var(rt| Ft-1)=Var(εt| Ft-1)，服从条件均值为μt、条件方差为ht的分布，在t时刻的扰动项为εt，当{rt}为平稳序列，根据GARCH模型，则扰动项εt满足以下条件[6]：

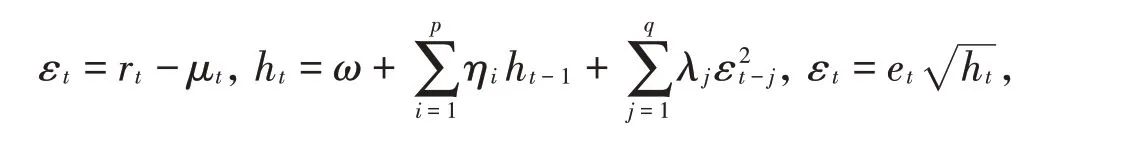
其中ω为截距项，q和p分别为ARCH项和GARCH项的滞后阶数，ηi和λj均非负。EGARCH模型就是在GARCH模型的基础上放松了参数非负的约束，并且引入了加权扰动函数，其中et～N(0,1)，且。通过构造特殊的函数，能对正负扰动进行非对称处理[7]，所以EGARCH模型结构为

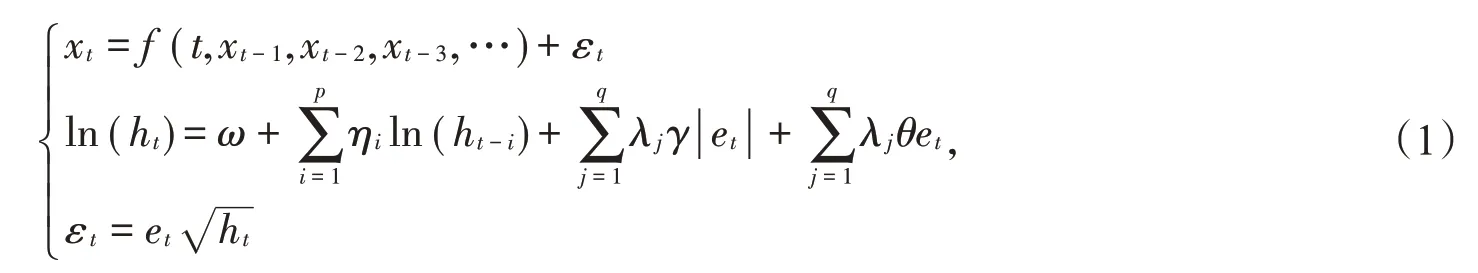
其中，令ηi=β，λjγ=α，λjθ=γ，若α不等于0，则说明具有非对称性[8]；若α小于0，则具有杠杆效应。

2 结合沪深300指数的实证分析

选取沪深300指数近17年里的工作日收盘价格数据，对其取对数和一阶差分，便得到其对应的对数收益率，图2为沪深300指数的对数收益率时序图。

由图2可以看出，对数收益率的序列没有明显的趋势特征，但是有集群效应，且这种集群效应主要集中在2008年前后、2015年前后和2018年后，结合收盘价的时序图（图1）可以看出，2008年时股市经历了一场增长较为迅速的牛市，然后又迅速转为熊市，接下来的几年里价格波动幅度较小且平稳，属于正常波动。2015年，股市又迎来了一波牛市，可随后又迅速下跌。2018年左右股票价格也有一次小幅度的波动。为了研究对数收益率序列的平稳性和随机性，对其进行平稳性和随机性检验，LB检验、ADF检验、LM检验、Portmanteau Q检验的P值分别为P<0.05、P<0.01、P<0.02、P=0.01304。由LB检验和ADF检验的P值可知对数收益率序列为平稳且非纯随机序列。

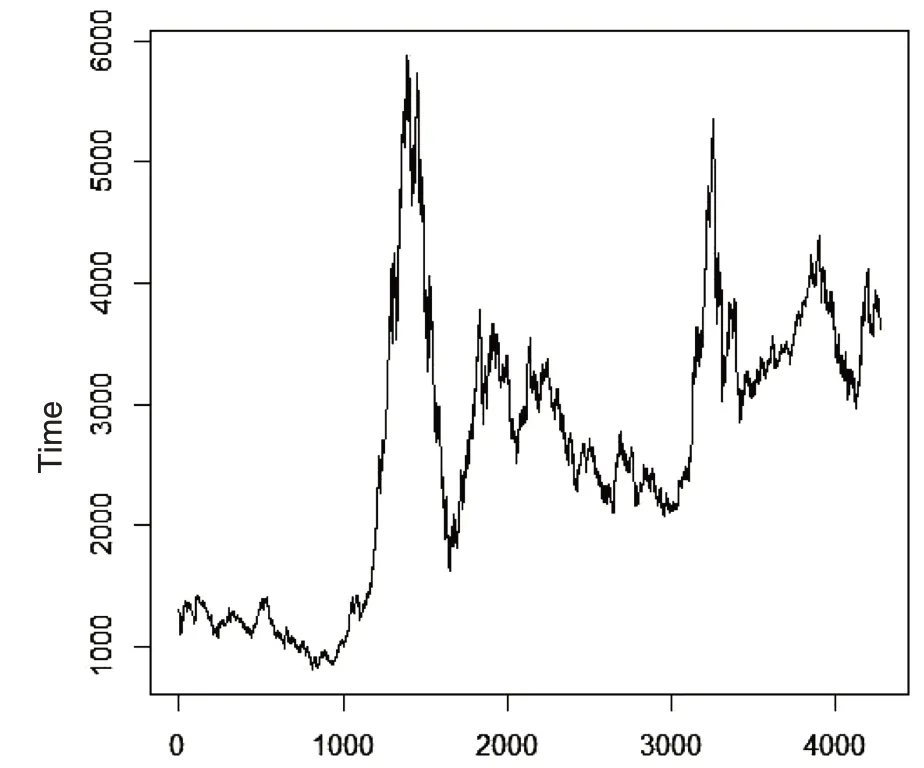
图1 工作日收盘价时序图

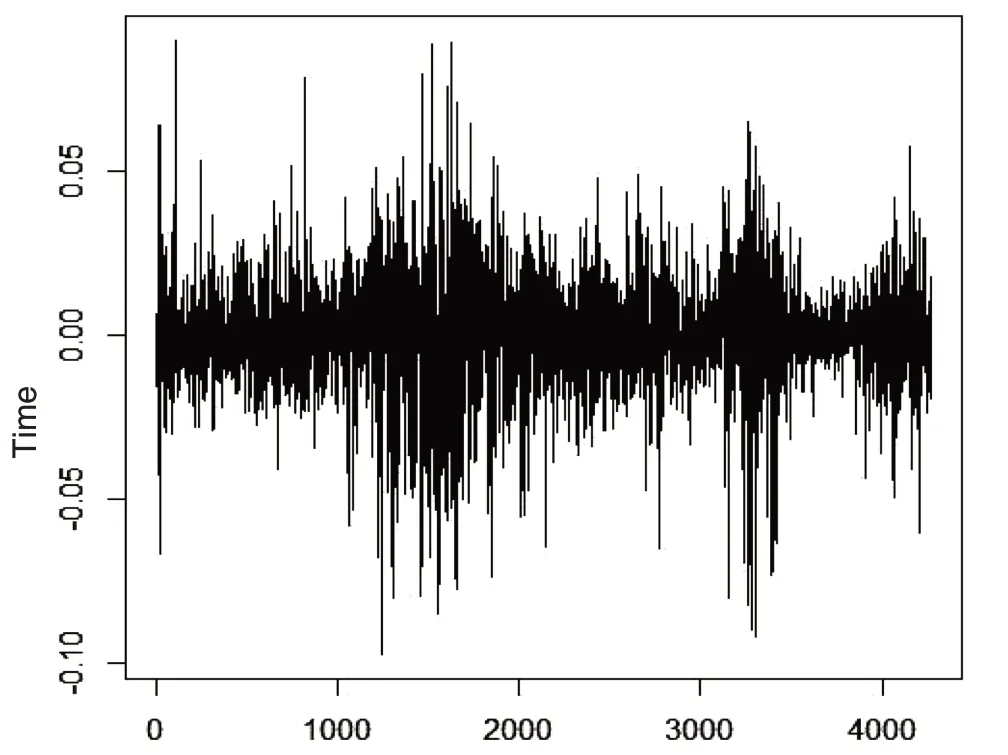
图2 对数收益率时序图

图3 为自相关数和偏自相关数。由图3可以看出，自相关和偏自相关系数图均有拖尾现象，且由图3（a）可以看出，该序列之间有较强的相关性，所以对其进行了ARIMA模型拟合。因自相关系数图和偏自相关系数图均有拖尾现象，而且每间隔3阶，自相关系数都在两倍标准差以内，所以对其进行了多个ARIMA 模型的拟合，分别对模型进行显著性检验，表1为各个模型的AIC值。

最后根据AIC准则选取了ARIMA(3，0，3)对确定性信息进行了提取。确定性信息模型口径为

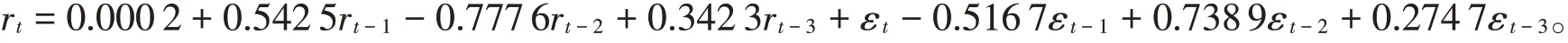
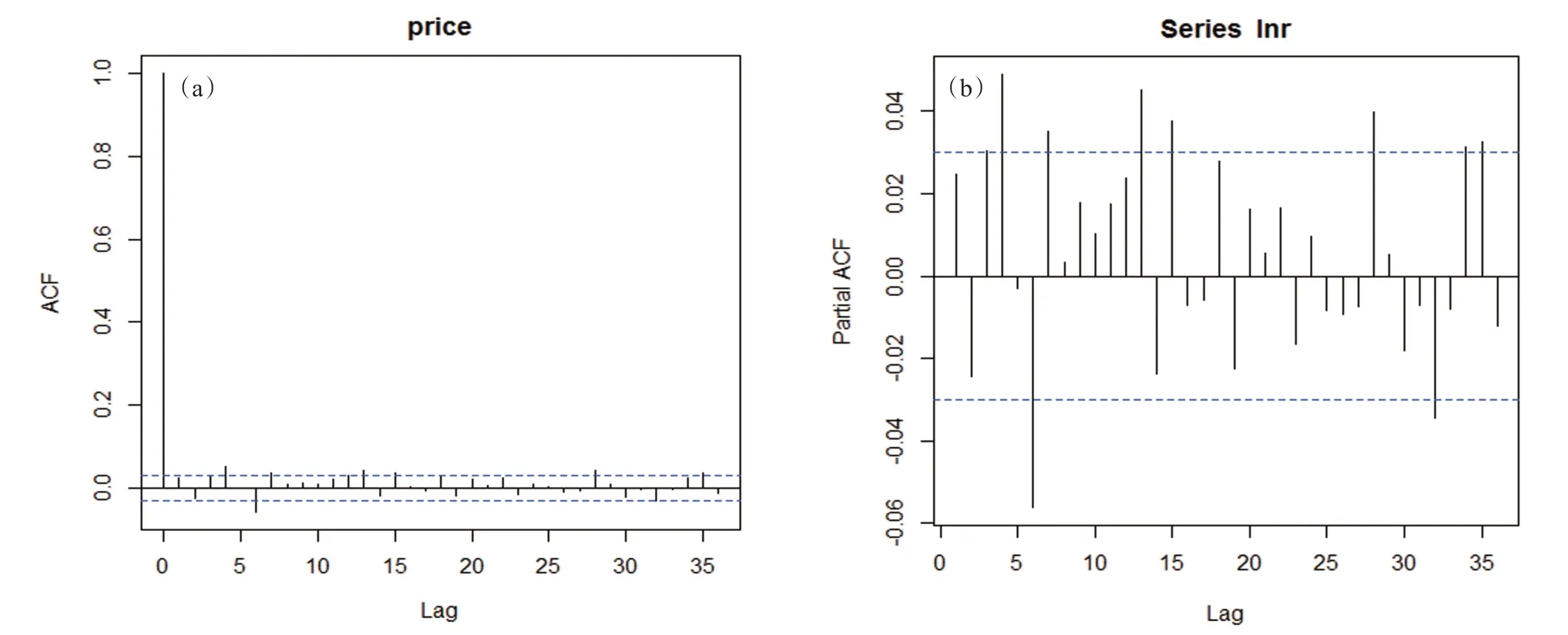
图3 （a）自相关系数；（b）偏自相关系数

表1 ARIMA模型AIC值

因为图1显示了较强的集群效应，所以对其进行ARCH 检验，这里分别进行了LM检验和Portmanteau Q检验，结果表明，该序列具有较强的ARCH效应，P值从一阶开始就远远小于0.05，可以确定该序列显著方差非齐且具有长期相关性。对该数据进行GARCH 模型拟合，这里选择了GARCH(1，1)、GARCH(1，2)和GARCH(2，1)进行拟合。表2是这3个模型的相关参数信息，通过对比筛选最后选择了GARCH(1，1)。表3 为GARCH(1，1)估计系数的统计特征。最后得出ARIMA(3，0，3)-GARCH(1，1)模型为

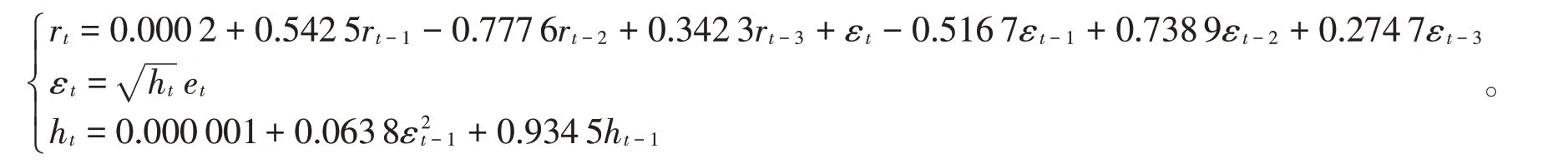
表2 GARCH(1,1)模型的AIC值

表3 GARCH模型相关统计量

利用上述模型，绘制出条件异方差的95%的置信区间，并与方差齐性的95%置信区间进行比较，如图4所示。图4中两条平行虚线为方差齐性得到的95%的置信区间，中间两条波动的实线是GARCH(1，1)模型得到的95%的置信区间。结合对数收益率的观察序列，可以看出，GARCH(1，1)模型得到的置信区间更加接近观察序列的真实波动情况，表明GARCH(1，1)模型拟合的效果较为准确。这样可以利用这个模型对接下来的收益率波动性情况进行短期预测，表4是模型的预测值。

表4 对数收益率预测值与实际值

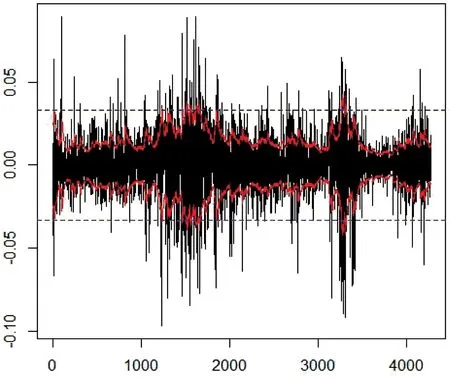
图4 条件异方差置信区间与方差齐性置信区间比较

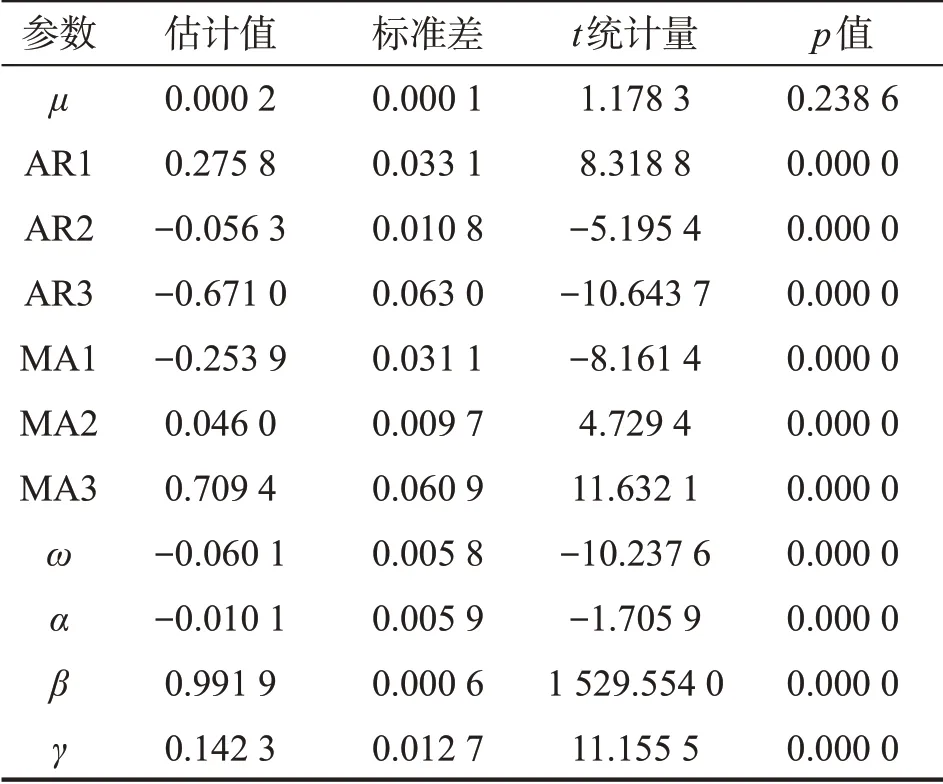
表5 ARMA(3，3)-EGARCH(1，1)模型的统计量

由表4可以看出，到13天后预测值开始收敛于一个固定值，这是因为ARIMA模型只适用于短期的预测与估计，随着预测时间的推移，GARCH模型的预测会收敛于方差齐性的值。但是，从前13天的预测值来看，在接下来的两周里，沪深300指数的收盘价格处于上涨阶段，通过与实际对数收益率的对比发现，预测结果与实际情况相似，进一步确定该模型效果显著。为研究沪深300指数的对数收益率是否具有杠杆效应，运用EGARCH 模型对其进行研究，利用R 语言对其进行模型拟合，表5 是ARMA(3，3)-EGARCH(1，1)模型的估计系数。

由表5可以得出，ARMA(3，3)-EGARCH(1，1)模型的表达式为

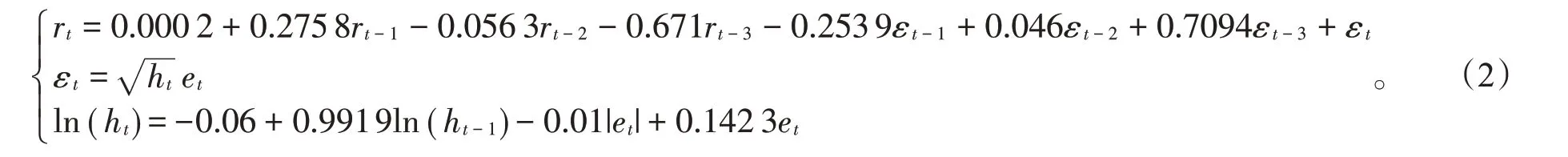
由式（2）可以看出α小于0，因而沪深300指数的对数收益率存在杠杆效应。

3 结论与建议

GARCH模型在发达国家的金融领域研究中颇为流行。由上面的实证分析可以看出，GARCH模型也适用于我国的金融市场的研究，并且由模型拟合的效果来看，我国股票市场收益率的波动性受异方差影响较为显著。结合EGARCH模型可以看出沪深300指数对数收益率存在杠杆效应，即负面冲击大于正面冲击效果，说明我国大部分企业都是选择负债筹资的方式进行融资。

应用GARCH 模型分析结果表明，在2008 年、2015 年和2018 年这些时间段里收益率的波动性比较大。2008 年我国正遭受金融危机，股票市场从2008 年之前的牛市一落千丈跌成熊市。2009 年到2014年，股票收益率的波动较为平稳，在此期间，中国经济发展缓慢，金融市场不断完善，再加上央行接二连三降息，终于在2015 年，股票市场又一跃进入了牛市阶段。为了进一步促进金融市场的发展，随即在2015年7月份证监会发布大小限禁售令，原本应该受益的沪深300指数，却接连下跌。在2018年，中国出台了近30项政策，其中包括降低许多行业的增值税税率和提高个人纳税水平线，目的是为了推动经济发展；金融监管政策集中转暖，目的是为了支持企业融资。可是由对数收益率的时序图可以看出2018年后波动性较大，这说明出台的政策并没有取得较大的成果。从2015年的波动性来看，这段时间的波动既不受金融危机的影响，又不受政策限制。与此同时，证监会发布了有利于沪深300指数的大小限禁售令，本应该受益的股票，却不断下跌，不难看出这是因为金融市场的监管制度不够完善、有人投机取巧所导致。2018年国家出台了这么多推动经济市场发展的政策，但是取得的效果甚微，这是因为金融监管政策在1月份密集出台，但是后续监管没跟上。

因此，建议尽快完善我国金融市场的监管体系，加大监管力度，使每一项有利于金融市场发展的政策都能有效执行。制定监管部门内部的行为准则，使每一个监管部门都能发挥作用，增加金融市场的信息透明度，增加对金融市场不法现象的举报途径，使每一个投资者和上市公司都能对市场起到监督作用。