金属色散模型对微纳结构FDTD计算的影响研究

刘 超，刘 瑜,2

（安徽大学1.电子信息工程学院，2.计算智能与信号处理教育部重点实验室，安徽合肥230601）

近年来，光与金属相互作用的表面等离子体特性引起了人们极大的兴趣[1]。1998年Ebbesen等人发现光透过金属薄膜孔洞阵列时发生异常透射增强现象[2]。随着纳米技术的发展，金属薄膜纳米孔阵列已逐渐成为表面等离子体共振（SPR）传感研究的重要结构[3]。人们通过时域有限差分（FDTD）方法研究金属纳米孔阵的表面等离子体光谱性质[4]。亚波长结构具有“场的局域性”和“模式的共振性”特点，计算结果对介质色散等媒质物理参数的变化异常敏感，强烈依赖于金属色散模型的精确程度。典型的金属色散模型有Drude模型、Lorentz模型、Drude-Lorentz模型及其扩展等。大多数色散模型需要通过增加一个或多个Lorentz谐振项来精确拟合金属介电响应过程，但增加更多的Lorentz项将导致FDTD算法实现困难、计算效率降低以及计算资源需求增加。为此，Drude临界点（Drude2cp）模型因其对金属色散更简洁精确的描述而在FDTD算法领域受到关注[5-6]。

本文首先讨论了几类典型的金属色散模型，以及基于辅助微分方程（ADE）处理金属色散介质的方法。然后比较分析了不同色散模型拟合银（Ag）介电系数的差异，在此基础上，利用FDTD方法对银纳米孔阵列透射特性进行建模计算，研究分析不同金属色散模型对FDTD仿真微纳结构电磁特性的精确性影响与差异。

1 金属色散模型与算法实现

不同的金属色散模型都是为了更好地描述给定条件下的介电响应过程，减小与实际金属介电效应的偏差。Drude模型基于金属自由电子气假设，在光子能量小于电子能带跃迁阈值情况下有效[7]，其表达式为

式中ε∞为无穷大频率时的介电常数，ωD为Drude频率，γ为碰撞频率。

L4（4-Lorentz-pole pairs）模型[8]和Drude-2Lorentz模型[6]都是在Drude模型基础上，增加Lorentz阻尼项，在有限波长范围内对金属的带间跃迁进行近似，其表达式如下：

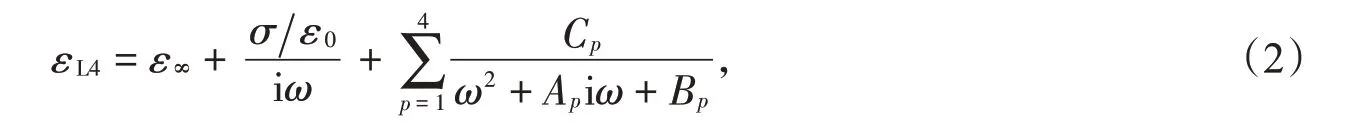
式中σ为电导率，ε0为真空介电常数，Ap，Bp，Cp为合并简化系数。

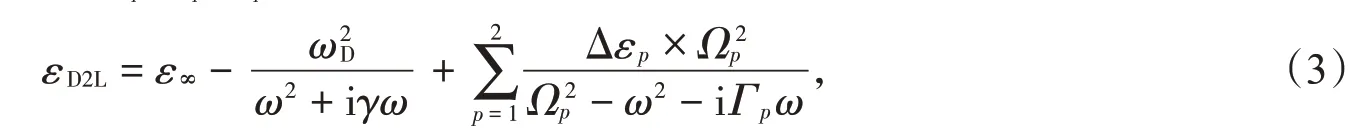
式中Δεp为静态和无穷大频率的介电常数之差，Ωp为振子固有频率，Γp为碰撞频率。

Drude2cp模型是在Drude模型基础上，添加两个根据能带理论分析得出的临界点（CP）项组成，可以有效拟合复杂的金属非对称线型带间跃迁[9]，其表达式如下：

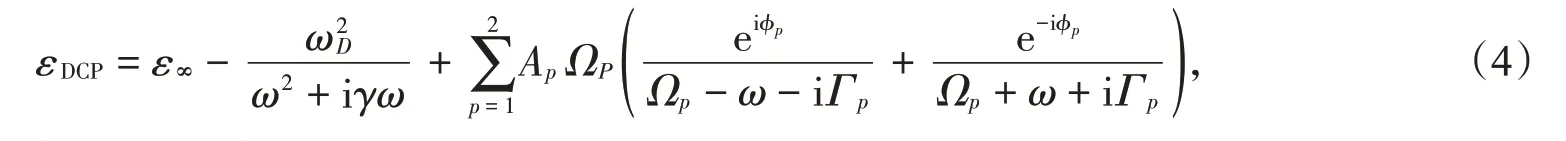
式中Ap为幅度，Ωp为能隙，φp为相位，Γp为极点的扩展。

利用ADE法处理上述色散模型，由时域麦克斯韦旋度方程：

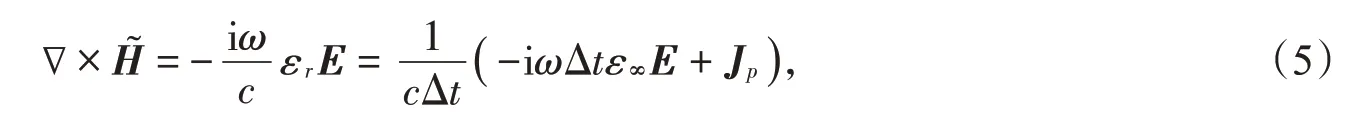
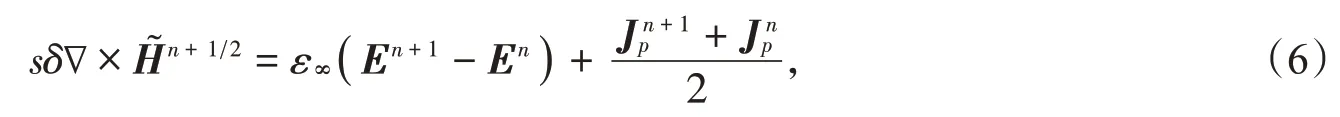
使用Drude模型时，其极化电流表示为

使用L4模型，其极化电流可表示为

使用Drude-2Lorentz模型，其极化电流可表示为

使用Drude2cp模型，其极化电流可表示为

其中，JD.p为Drude项极化电流，将Drude项与增加的Lorentz或CP项的极化电流离散成如下形式[8]：

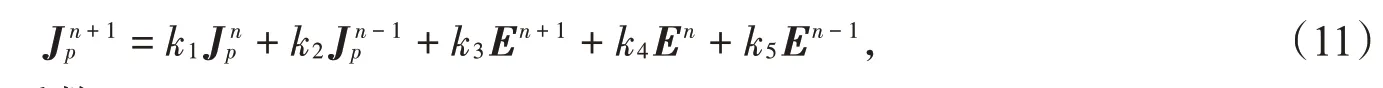
其中k1、k2、k3、k4、k5为差分离散系数。

由式（7）～（11）可知，不同色散模型中随着极化电流多项式项数的增加，将造成离散递推困难，从而大幅增加FDTD算法的实现复杂度。

联立式（6）～（11）可推导出电场En+1的FDTD递推方程，再由法拉第电磁感应定律可推导出的递推式。

2 不同色散模型的算法差异

2.1 Ag的介电系数

以金属Ag为例，由图1（a）、（b）可知：1）波长在200 nm～1 000 nm时，不同色散模型Ag介电系数的实部差异较小，虚部差异明显；2）Drude-2Lorentz、Drude-4Lorentz和L4三条曲线表明，Lorentz谐振项的项数与介电系数拟合值的精确性并不是线性对应的关系，简单的增加Lorentz项并不能进一步提高介电系数的精确性；3）波长200 nm～1 000 nm的宽频段范围内，在Drude模型基础上添加根据能带理论分析得出的临界点（CP）项构成的Drude2cp 模型最接近实际测量的金属Ag（JC）介电系数。由于在Ag 的能带边沿附近，电子很容易发生带间跃迁，不同色散模型对内部能带跃迁描述的差异导致与实际Ag介电系数之间的偏差，从而限制了Ag的不同色散模型在近红外和可见光频段的计算精确性。对于大部分贵金属，当光子能量超过1 eV时，金属就会出现带间跃迁效应，使得以自由电子气假设为基础的Drude模型及其修正扩展与实际金属之间产生明显偏差。

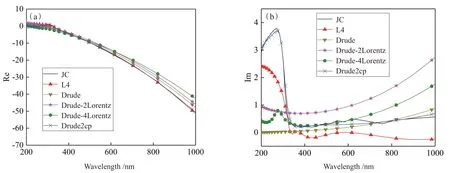
图1 （a）Ag介电系数的实部；（b）Ag介电系数的虚部

2.2 计算模型设置

利用FDTD算法模拟Ag纳米孔阵列的透射特性，分析不同色散模型计算的差异。纳米孔阵列结构模型如图2所示。基底材质为玻璃，厚度d1=1 000 nm，折射率为1.45。圆孔阵列的周期Lx=Ly=400 nm，单个圆孔直径D=200 nm，圆孔填充介质的折射率为1.4，银膜厚度d2=100 nm。光源的波长范围为200 nm～1 000 nm，沿Z 轴正方向入射，X 轴偏振。在x，y 方向上设置周期性边界条件，z 方向上设置PML。FDTD仿真区域设置为400 nm×400 nm×600 nm。

Ag纳米孔阵列的透射率定义为

其中Pin和Pout分别为入射光光强、透射光光强。

2.3 计算结果分析

银纳米孔阵列是一个比较典型的金属微纳表面等离子体共振（SPR）激发结构，当满足色散关系时，入射光与金属薄膜表面等离子体之间的共振耦合相互作用，使纳米孔阵列出现透射增强现象[10]。利用FDTD算法进行模拟，定义相对透射率误差为

其中Tmodel为色散模型共振峰处的透射率，TJC为实际金属Ag共振峰处的透射率。图3为所计算的不同色散模型的Ag纳米孔阵列的透射谱。

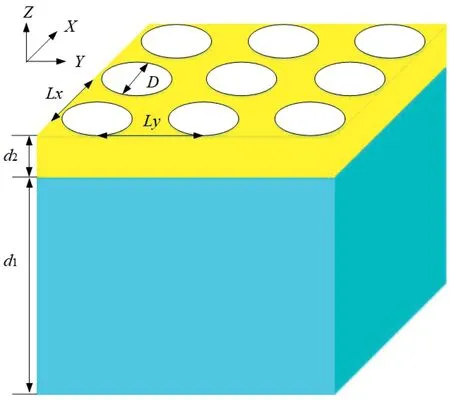
图2 纳米孔阵列结构模型

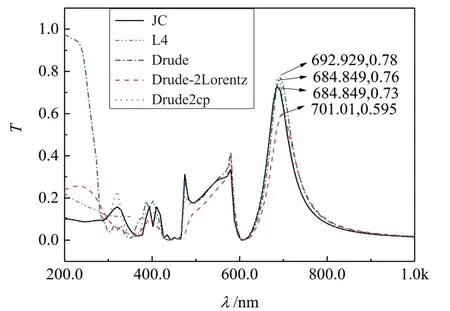
图3 不同色散模型的Ag纳米孔阵列的透射谱

从图3可看出，实际金属Ag（JC）的共振透射率为0.73，透射谱共振波长为684.849 nm，共振峰半峰全宽为59.55 nm；Drude模型的透射率为0.78，相对透射率误差为6.85%，透射谱共振波长为692.929 nm，半峰全宽为60.27 nm；Drude-2lorentz模型的透射率为0.595，相对透射率误差为18.49%，透射谱共振波长为701.01 nm，半峰全宽为69.91 nm；Drude2cp模型的透射率为0.76，相对透射率误差为4.11%，透射谱共振波长为684.849 nm，半峰全宽为58.92 nm；而L4 模型当波长大于350 nm 时，Ag 介电系数的虚部小于零，导致FDTD仿真结果发散，其中在波长200 nm～350 nm之间，不满足共振条件。因此，FDTD计算透射谱精细结构的计算精度与金属银的色散模型直接相关。从数值实验分析可得：1）自由电子假设导出的Drude色散模型，通过增加Lorentz项（Drude-2Lorentz和L4模型）并不能减小相对透射率误差，这与前述Lorentz谐振项的项数与介电系数拟合值的精确性不是线性提高关系的结论一致。由于金属带间跃迁的复杂性，通过在自由电子假设基础上增加阻尼谐振项，对金属银的介电响应过程进行拟合近似，如图1所示，仅仅在非常有限的波长范围内有效。2）由能带理论分析修正的Drude2cp模型具有更好的计算精度，在更宽的波长范围内能够拟合金属银的介电响应过程，同时，Drude2cp模型的极化电流多项式相对于Drude模型仅仅增加两项，不会大幅增加FDTD算法实现的复杂度。

3 结 论

金属微纳结构的FDTD 计算结果强烈依赖于色散模型的精确性。Drude2cp 模型能够在更宽的频带内拟合金属银的介电响应过程，在仿真精细结构时，具有更好的计算精度，且不会进一步增加算法复杂度。考虑到FDTD算法是一种时域方法，在宽频带范围内对介电系数多项式的差分离散可行性和精确性有明确要求，因此，为实现微纳结构的FDTD精确仿真，通过固体能带理论修正金属色散模型，添加临界点（CP）项得到Drude2cp模型，比单纯增加阻尼谐振项的修正方法更加有效可行。