一类具有单理想的Hom-李代数的结构
李小朝
(黄淮学院数学与统计学院,河南驻马店463000)
Hom-李代数是Hartwig,Larsson和Silvestrov在2006年研究Witt代数和Virasoro代数的形变理论时提出来的[1],它是把李代数的Jacobi等式通过线性映射进行扭曲而得到的新的代数结构。Hom-李代数是李代数的一种形变或推广。早期的李代数的形变研究见胡乃红给出的q-李代数[2]。由于Hom-李代数与理论物理、量子群等有着紧密的联系,自被提出以来,就得到广泛和深入的研究,如Hom-李代数及其同调理论[3],具有对称不变双线性型的Hom-李代数[4]等。陈良云等研究了Hom-李代数的广义导子[5],并给出Hom-李型代数的最新研究成果[6]。生云鹤研究了Hom-李代数的表示等[7]。有限维Cartan型李代数的保积Hom-结构及复半单李代数的Hom-代数结构[8-10]等已经被系统研究且得到了较好的研究成果。但是由于Hom-李代数所用线性映射的多样性,其结构和分类问题非常复杂。本文通过复数域ℂ上单李代数构造单保积Hom-李代数,研究理想为3维单保积Hom-李代数的4维Hom-李代数,给出这类Hom-李代数的非李代数结构。
1 预备知识
定义1[1,7]设L 是复数域ℂ 上一个线性空间,α:L →L 是一个线性映射。若二元运算L×L →L:(x,y)→[x,y]是双线性的,且对∀x,y,z ∈L 满足:(1)[x,y]=-[y,x],(2)[α(x),[y,z]]+[α(y),[z,x]]+[α(z),[x,y]]=0,称三元组(L,[,],α)是一个Hom-李代数。条件(2)中的等式称为Hom-Jacobi等式。若还满足α([x,y])=[α(x),α(y)],则称(L,[,],α)为保积Hom-李代数。
定义2设(L,[,],α)是一个Hom-李代数。若L 的子空间L1满足α(L1)⊆L1, [L1,L1]⊆L1,称(L1,[,],α|L1)是(L,[,],α)的Hom-子代数。若L的子空间L2满足α(L2)⊆L2, [L2,L]⊆L2,称(L2,[,],α|L2)是(L,[,],α)的理想。
定义3设(L,[,],α), (L,[,]′,α′)是两个Hom-李代数,f:L →L是一个线性映射。若对∀x,y ∈L,都有f ([x,y])=[ f (x),f (y)]′和f ∘α=α′∘f,称f 是一个Hom-李代数同态。特别地,若f 是可逆的线性映射,则称f是一个Hom-李代数同构,而Hom-李代数(L,[,],α),(L,[,]′,α′)是同构的。
2 具有3维单理想的4维Hom-李代数
以3维单李代数L=sl2(ℂ)为基础,给出3维单保积Hom-李代数(L,[,],α),进而研究以3维单保积Hom-李代数(L,[,],α)为理想的4维非李代数的Hom-李代数的结构。
设{e,f,h}是L=sl2(ℂ)的标准基,即[e,f ]=h, [h,e]=2e, [h,f ]=-2f,所考虑的矩阵也是在此基下的矩阵。由于α 是单李代数L=sl2(ℂ)的自同态,则α=0 或者α 是自同构。下面假定研究的L=sl2(ℂ)的自同态不为零,即是自同构。由文献[9]的命题2.1知,保积Hom-李代数(L,[,],α)与(L,[,],β)同构当且仅当α,β是共轭的。因此给出L上的自同构只需考虑其共轭类的代表元即可。在同构的意义下有如下结论。
命题1[10]设(L,[,],α)是一个保积Hom-李代数,则α=id或者α(e)=-e,α( f )=-f,α(h)=h。
这样以3 维单李代数L=sl2(ℂ)为基础,得到3 维单保积Hom-李代数(L,[,],α),其中α=id 或者α(e)=-e,α( f )=-f,α(h)=h。接下来考虑以上述3维单保积Hom-李代数(L,[,],α)为理想的4维非李代数的Hom-李代数(g,[,],σ)。设g=span{e,f,h,x},由于 [L,g]⊆L,则可以设

由定义2知,σ|L=α,σ在基{e,f,h,x}下对应的矩阵为
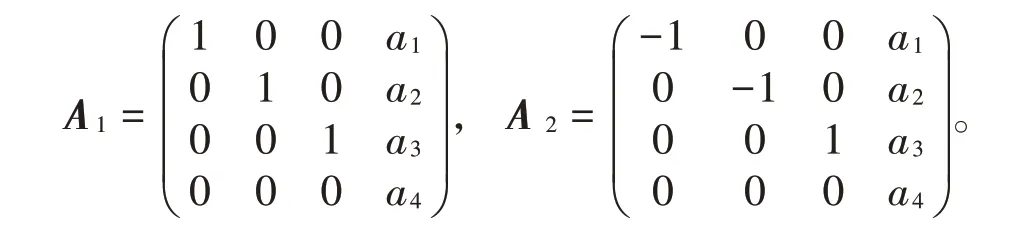
对A1,可以选择适当的元素x,使得A1对应情形分别为
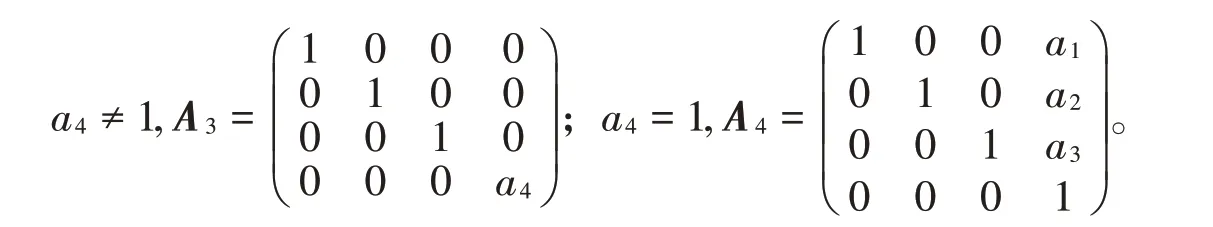
定理1设(g,[,],σ3)是一个Hom-李代数,但(g,[,])不是李代数,则有如下结论:
(1)[x,e]=e, [x,f ]=f, [x,h]=h,σ3对应的矩阵为A3=diag(1,1,1,2);
(2)[x,e]=c11e+c12f +c13h,[x,f ]=c21e+c11f +c23h,[x,h]=2c23e+2c13f -2c11h, σ3对应的矩阵为A3=diag(1,1,1, -1),c11、c12、c13、c21不全为零。
证明由于(g,[,],σ3)是一个Hom-李代数,则有元素x、e、f满足Hom-Jacobi等式,即

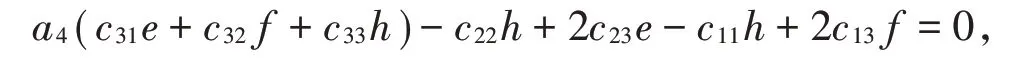

同理,元素x、e、h满足Hom-Jacobi等式,有

元素x、f、h满足Hom-Jacobi等式,有

由式(3)(4)(8)可得:(a4-2)(a4+1)c33=0;由式(1)(9)可得:(a24-1)c31=0;由式(2)(6)可得:(a24-1)c13=0。
综上对a4进行讨论,注意到a4≠1。
若a4≠2且a4≠-1,则c13=c31=c33=0,进而得cij=0(1≤i,j ≤3)。此种情形(g,[,])是李代数,舍去。
若a4=2,则c13=c31=0,进而还有c21=c12=c32=c23=0,c11=c22=c33。容易验证c11≠0时,(g,[,])不是李代数。取适当的x可以得到[x,e]=e, [x,f ]=f, [x,h]=h。
若a4=-1,则,相应的运算为
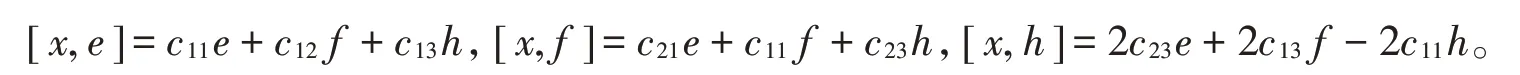
容易验证系数c11、c12、c13、c21不全为零时,(g,[,])不是李代数。
定理2设(g,[,],σ4)是一个Hom-李代数,σ4对应的矩阵为A4,则(g,[,])是李代数。
证明与定理1的证明过程类似,可以得到a1=a2=a3=0,即σ4=id,此时Hom-李代数(g,[,],σ4)是李代数(g,[,])。
同样对A2,可以选择适当的元素x,使得A2对应情形分别为

定理3设(g,[,],σ5)是一个Hom-李代数,但(g,[,])不是李代数,则有:[x,e]=e, [x,f ]=f, [x,h]=-h,σ5对应矩阵为A5=diag(-1, -1,1,2)。
证明由于(g,[,],σ5)是一个Hom-李代数,则有元素x、e、f满足Hom-Jacobi等式,得
同理,元素x、e、h满足Hom-Jacobi等式,可以得到

元素x、f、h满足Hom-Jacobi等式,可以得到
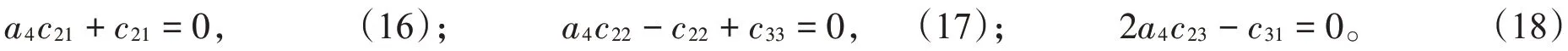
由于a4≠±1,故c12=c21=0。由式(10)(18)得到c31=c23=0;由式(11)(15)得到c13=c32=0;由式(12)(13)(17)可得(a4-2)(a4+1)c33=0。
如果a4≠2,则c33=0,进而c11=c22=0,此时(g,[,])是李代数,舍去。
如果a4=2,则有c11=c22=-c33。若c11=0,(g,[,])是李代数,舍去。因此这里设c11≠0,取适当的x,可以得到[x,e]=e, [x,f ]=f, [x,h]=-h。
对A6、A7有类似的结论,证明过程略。
定理4设(g,[,],σ6)是一个Hom-李代数,但(g,[,])不是李代数,则有:(1) [x,e]=0, [x,f ]=h, [x,h]=2e, σ6对应矩阵为A6=diag(-1, -1,1,1);(2)[x,e]=h, [x,f ]=c23h, [x,h]=2c23e+2f,σ6对应的矩阵A6=diag(-1, -1,1,1),其中c23为任意常数。
定理5设(g,[,],σ7)是一个Hom-李代数,但(g,[,])不是李代数,则有:(1)[x,e]=e+c12f, [x,f ]=c21e+f, [x,h]=2h,σ7对应的矩阵A7=diag(-1, -1,1, -1),其中c12、c21为任意常数;(2)[x,e]=f, [x,f ]=c21e,[x,h]=0, σ7对 应 的 矩 阵A7=diag(-1, -1,1, -1), 其 中c21为 任 意 常 数;(3) [x,e]=0, [x,f ]=e,[x,h]=0,σ7对应的矩阵A7=diag(-1, -1,1, -1)。
3 结束语
Hom-李代数由于所用线性变换形式多样,其结构较为复杂。利用李代数的形变得到Hom-李代数是很常用的,这种Hom-李代数的结构研究比较方便。本文研究了以3 维单保积Hom-李代数为理想的4 维Hom-李代数,并给出了具体的结构。利用已知Hom-李代数扩充出新的Hom-李代数是值得探索的方法。

