涉及水平分量的磁场微极流方程组的正则性准则
许 娟,张 辉
(安庆师范大学数理学院,安徽安庆246133)
在ℝ3中磁场微极流方程组描述如下:
在无穷远处假设

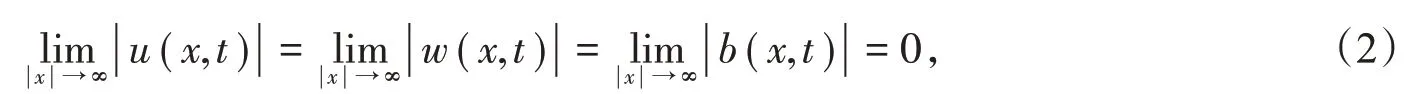
其中,u(x,t)∈ℝ3,表示未知的速度场;b(t,x)∈ℝ3,表示未知的磁场;w(t,x)∈ℝ3,表示微旋转速度场;p(t,x)∈ℝ,表示未知的压力;(u0,w0,b0)是给定的初始值,且在分布意义下满足∇⋅u0=∇⋅b0=0。
磁场微极流方程组是非常重要的流体力学方程组,它不仅反映了重要的物理现象,而且结构上还耦合了许多重要的流体力学方程组,如(Magneto-hydrodynamics)(MHD)方程组、微极流方程组、Navier-Stokes方程组等。类似于Navier-Stokes方程组的解的情形,在文献[1-2]中已经论证了方程组在三维情形下强解的局部存在性与Leary-Hopf型弱解的整体存在性。一个自然的想法就是能否将Navier-Stokes方程组的一些正则性准则或爆破准则推广到磁场微极流方程组。最近有一些文献[4-8]研究了磁场微极流方程组弱解的正则性准则和强解的爆破性准则,但是,需要指出的是,在讨论部分分量正则性准则时,会出现许多本质上的困难,这是由于速度场和磁场以及微旋度场的非线性耦合。
1 磁场微极流方程组的正则性准则
本文的目的是讨论带有部分速度分量和磁场分量的正则性准则。研究的动机来源于不可压Navier-Stokes 方程组和MHD 方程组的相关研究,文献[9-10]对Navier-Stokes 方程组给出了只涉及速度场水平分量的正则性准则:

文献[11]对MHD方程组给出了涉及速度场和磁场的部分分量的正则性准则:
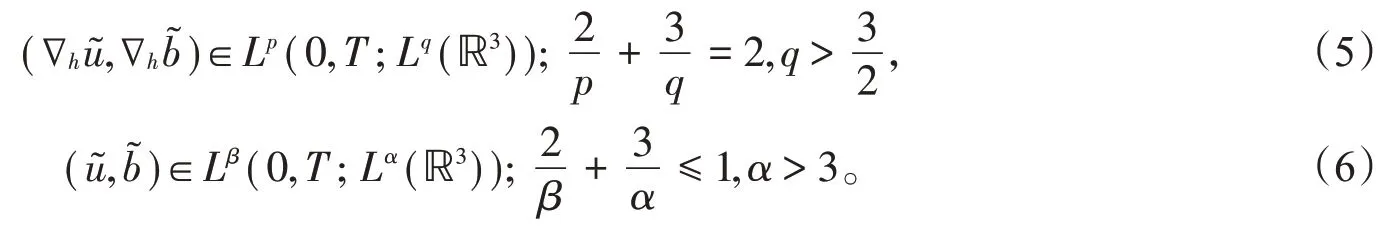
一个自然的想法就是探讨式(5)(6)能否推广到磁场微极流方程组。通过能量估计的方法获得了如下结论。
定理1假设初值(u0,w0,b0)∈H1(ℝ3),且在分布意义下有div u0=div b0=0,三元函数(u,w, b)是磁场微极流方程组(1)(2)的弱解,如果满足
则(u,w, b)在存在区间[0,T)上是唯一的强解。
注1磁场微极流方程组在一定条件下可以退化成Navier-Stokes方程组和MHD方程组,因此定理1的结论是Navier-Stokes方程组和MHD方程组相关结果的推广。
注2 正则性准则与微旋度场无关,对应的微极流方程组

在无穷远处假设

那么定理1又蕴含着如下的正则性准则。
定理2假设初值(u0,w0)∈H1(ℝ3),二元函数(u,w)是方程组(9)(10)的弱解,且满足:

则(u,w)实际是存在区间[0,T)上的唯一强解。
注3为了简便,本文中函数的Lp范数用‖ · ‖p表示,Hs范数用‖ · ‖Hs表示,常数用C表示,它可能涉及某些已经假定的量,如初值。
2 光滑解的先验估计证明
为了证明定理,先对光滑解给出如下的先验估计。
引理令(u,w, b)是方程组(1)(2)在[0,T)上的光滑解,若满足条件(7)或(8),则有

证明将方程组(1)中u-方程、w-方程、b-方程分别与-Δu、w、-Δb做L2内积,则有

下面对式(12)进行逐项估计,对于I1项,由[9-10]并结合Ho¨lder不等式和Young不等式有

其中,指标满足如下条件:

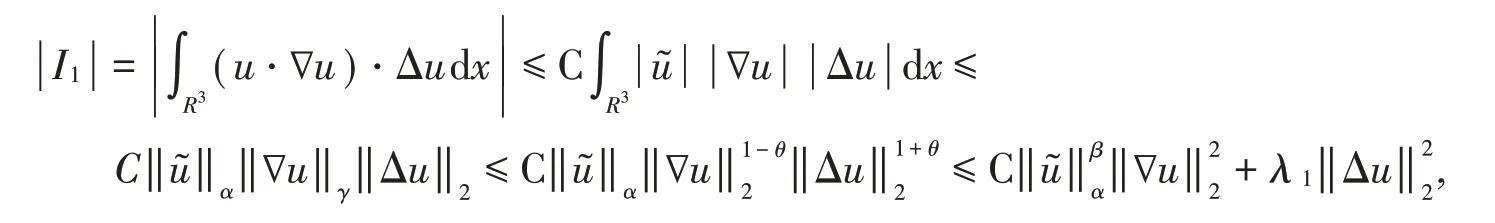
其中,指标满足下面条件:
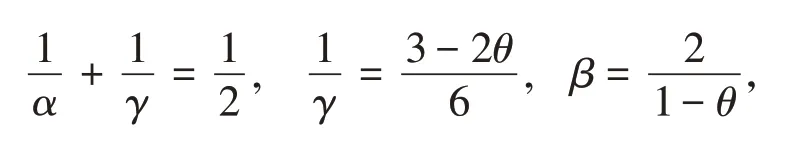
接着估计I2。将I2分解成2个部分:
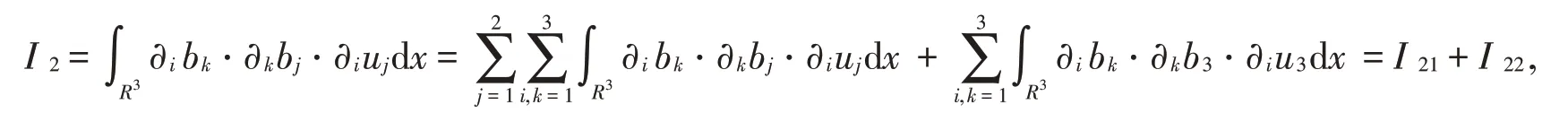
结合Ho¨lder不等式和Young不等式将I21、I22两项分别估计如下:

I2还可以这样估计,先将I2分解成4个部分:
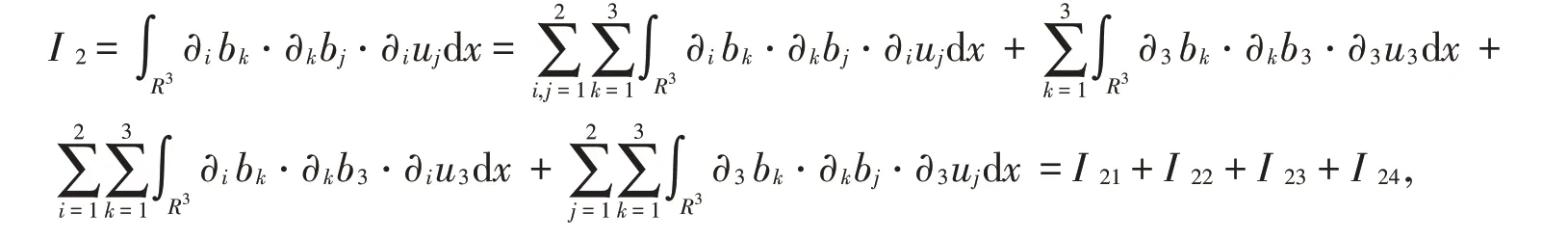
然后对这4项分别估计如下:
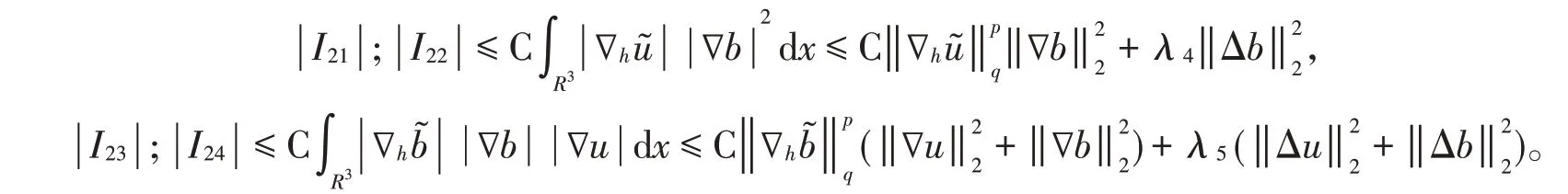
由于I3,I4在形式上与I2类似,所以省略两种具体的分解方法,有

最后,我们估计I5,I6。利用Ho¨lder不等式和Young不等式有

同时利用Gagliardo-Nirenberg不等式
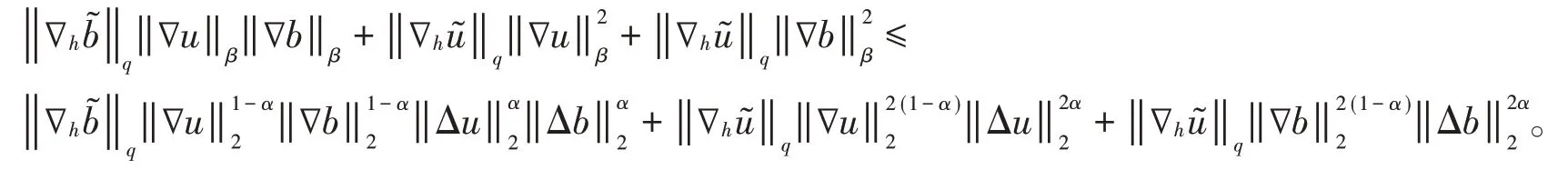
且通过适当选取参数λi,i=1,2,3,…,9,并综合上面的各式便可得到:

或者

利用Gronwall不等式,立即可以得到引理的证明。
3 正则性准则的证明
由于磁场微极流方程组的弱解如果满足H.da Veiga型准则,则弱解是[0,T]上的强解。具体地说,原保全[4]给出了如下的正则性准则:

上述结果表明,方程组解的奇性可以由速度场单独控制,因此只要能够说明在条件(7)或(8)下,速度场满足式(13),则完成定理的证明。通过一个标准的光滑过程,并结合引理的结论,可以得出当方程组(1)(2)的弱解满足条件(7)或(8)时,速度场∇u ∈L∞(0,T;L2(ℝ3)),至此完成定理的证明。
4 结 论
本文研究了磁场微极流方程组的正则性准则问题,利用能量估计的方法证明了速度场和磁场的水平方向满足条件
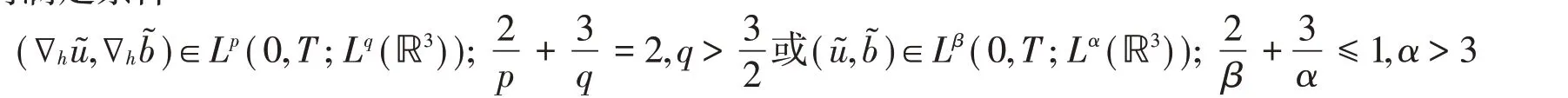
时,弱解在(0,T]上便是唯一的强解。结果表明,可以仅通过部分的速度场和磁场的分量来控制方程的奇性发展,这个结果展示了微旋度场似乎是一个“好”的物理量。

