基于神经网络光子晶体能带的计算

方云团，周秋百

（江苏大学计算机科学与通信工程学院，江苏镇江212013）

1987 年Eli Yablonovitch[1]和Sajeev John[2]分别在研究周期性光学结构时各自独立地提出了光子晶体的概念。光子晶体是一种利用两种或两种以上不同介电常数的材料在空间中进行周期性排列形成的晶体结构[3]。光子晶体最显著的特点就是光子带隙[4]（Photonic band gap，PBG）。光子晶体在TE模和TM模两种偏振态下具有不同的能带结构。TE 模带隙和TM 模带隙交叠部分称为完全光子带隙。虽然三维光子晶体在任意方向上都可存在光子带隙，但其制造困难[5]。相对而言，二维光子晶体容易制造，有着广泛的应用。对二维光子晶体传输特性的研究具有重要的理论意义和应用价值，对其研究的方法主要有平面波展开法[6]（Plane wave expansion method，PWE）和时域有限差分法[7]（Finite difference time domain method，FDTD）。近年来，随着神经网络的兴起，Asano T[8]和Inampudi S[9]等人将神经网络用于对光子晶体的研究。值得注意的是，Liu D[10]将利用神经网络进行反向设计的思想引入到光子晶体的研究中。本文旨在讲述完整的光子晶体神经网络建模过程，以正方晶格为研究对象，利用平面波展开法来获得数据集，然后训练神经网络（Neural network），最终实现用神经网络来计算光子晶体的能带。

1 模型的数据集

选择如图1所示的晶胞结构，晶胞边长为a，共计有4个自变量r1、r2、θ和d以及一个因变量归一化频率ω(2πc a)，其中r1与r2为两个介质圆柱的半径、d为圆心距离、θ为两圆心方向的方位角、c为光速。

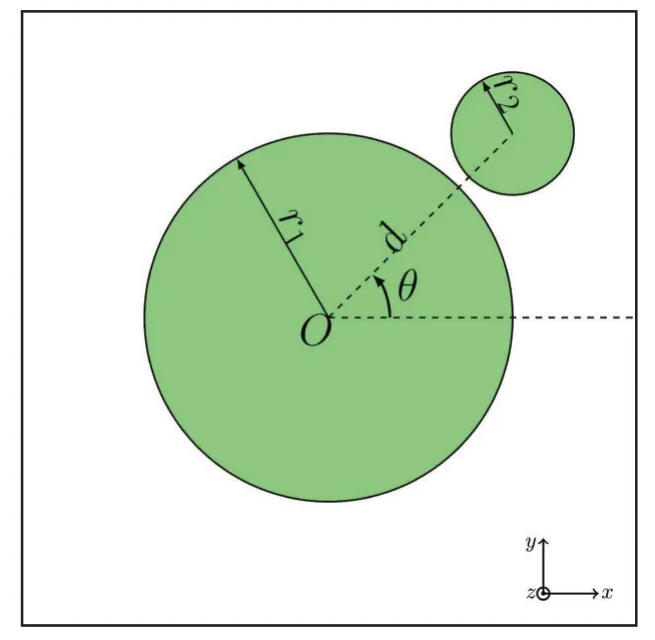
图1 晶胞结构

光子晶体的介电常量ε(r)，考虑E极化电磁波,电场矢量只有一个z分量，电场E(r)的全矢量波方程可以被写成：

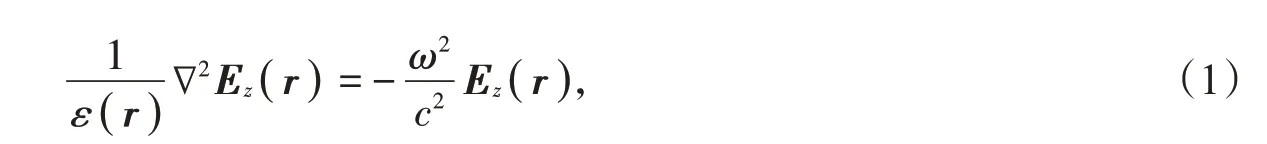
根据布洛赫定理，E(r)在周期性晶胞中可以被写成如下形式：

其中，Φ(r)随着晶格周期发生周期性改变，K是布洛赫波矢。

考虑到研究问题的周期性，利用布洛赫定理可以将电场展开成平面波之和：

其中，G是倒格子空间描述周期性结构的的晶格矢量，E(K+G)是关于G的展开系数。

周期性介质中，介电常数可以展开成傅里叶级数[11]：

其中

在式（5）中，Au为晶胞的面积。

对第一布里渊区每一个波矢K建立关于E(K+G)的线性方程组：

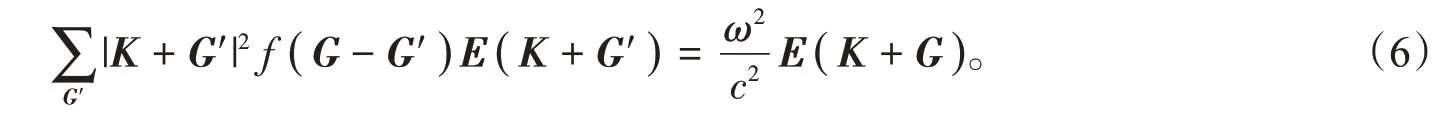
该线性方程组可看作矩阵特征方程，由特征值求得模式频率，得到光子晶体的能带结构，从而获得训练神经网络的样本数据。在进行神经网络训练之前，需要检查该模型是否能够利用神经网络得出结果，即需要满足通用近似定理[12]：一个包含足够多隐藏层神经元的多层前馈网络，能以任意精度逼近任意预定的连续函数。该定理表明：a.可以设计一个神经网络尽可能好地去“近似”某个特定函数，而不是说“准确”计算这个函数（我们通过增加隐藏层神经元的个数来提升近似的精度）；b.被近似的函数必须是连续函数。如果函数是非连续的，也就是说有极陡跳跃的函数，那神经网络就“爱莫能助”了。

将训练集可视化得到图2，没有一对多或极陡跳跃的情况，因此该模型是可以用神经网络来计算的。由图2(a)可以得出参数d对最终结果的影响力有限，因此我们得到如图3所示的神经网络结构。由图2(b)，可以得出参数θ的变化会导致结果正弦变化；图2(c)、(d)表明，r越大，频率越大。

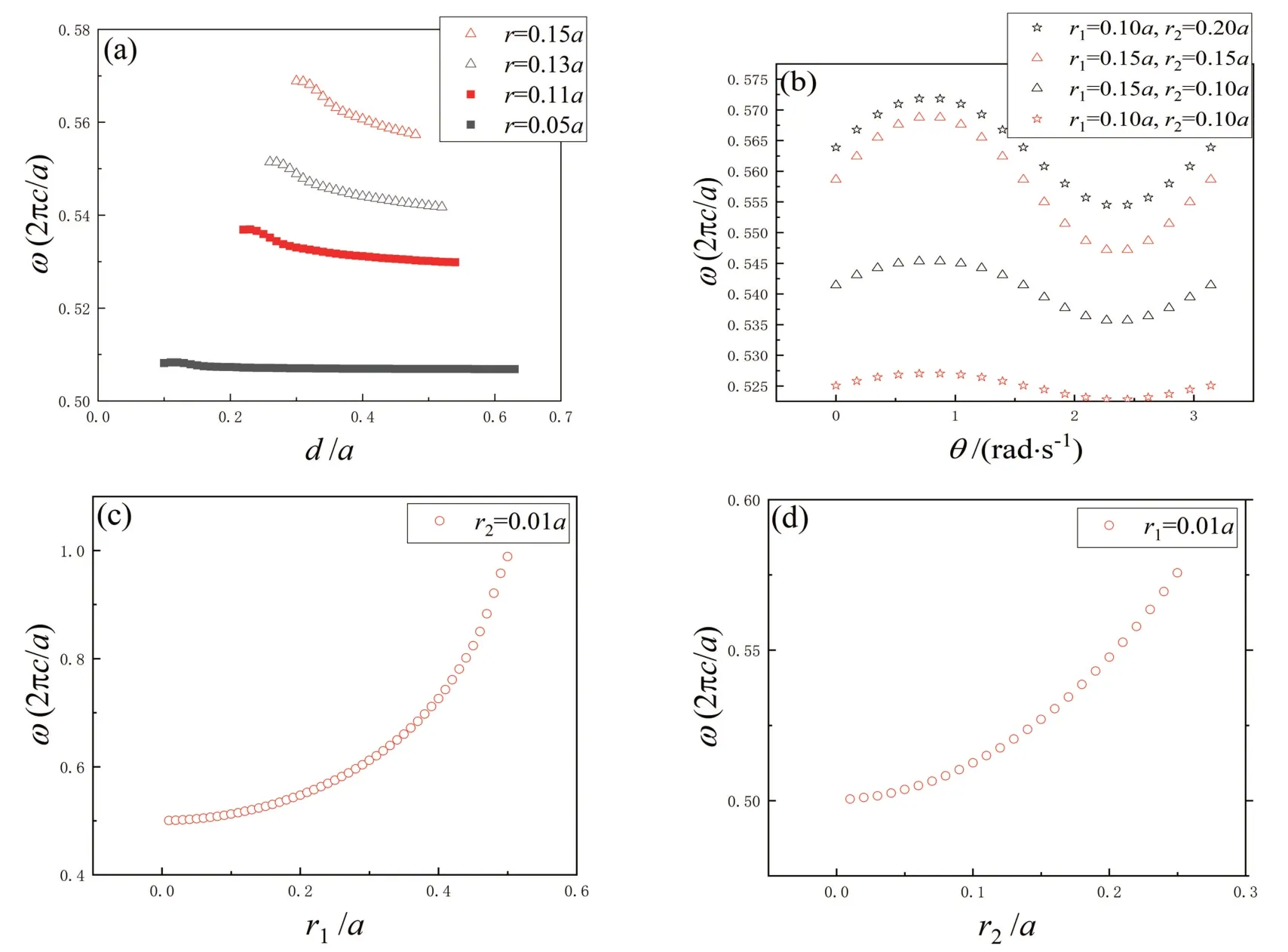
图2 连续函数的验证。

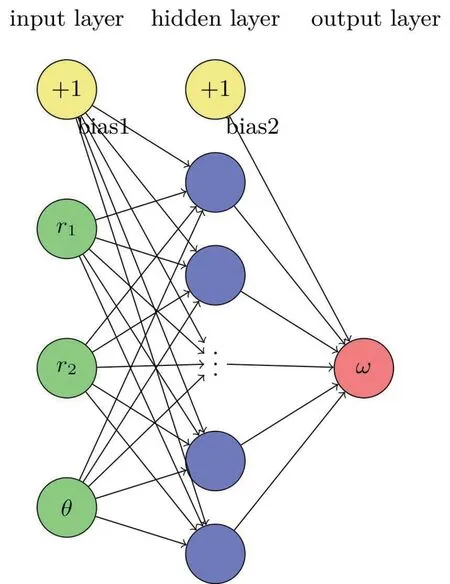
图3 神经网络的结构示意图

2 神经网络的训练

本文中激活函数为S函数，（如图4所示）。

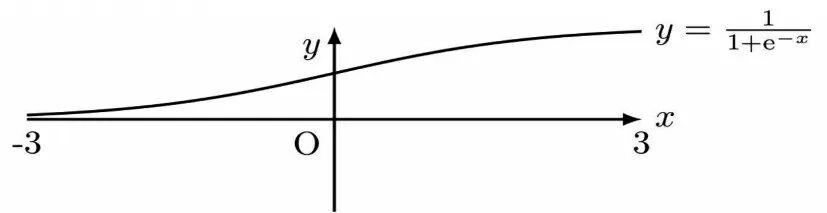
图4 Sigmoid函数

S函数只对绝对值小的输入值敏感，因此在训练之前需要对每一列进行归一化，具体如式（7）所示：

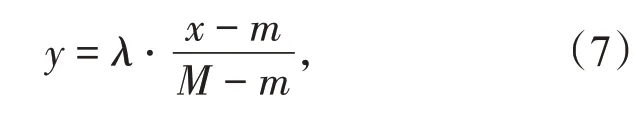
其中x 为原始数据，m 为一列的最小值，M 为一列的最大值，y 为归一化后的值，λ 为归一化系数，取值0.8。对于λ 的取值，正常情况下选择1，但在建模过程中我们发现取值为0.8 的时候会得到更优解。归一化之前需要得出最小值和最大值，以备反归一化时使用。所有数据集中，80%作为训练集，20%作为测试集，在数据集拆分之前，乱序是有必要的。

在本次示例中所使用的神经网络算法是BP（Back-propagation）算法[13]，分为前向传播和后向传播两个部分，如图5所示（相关符号请参照此图）。

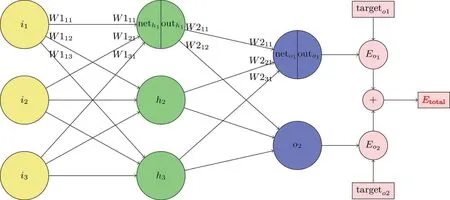
图5 BP算法结构示意图

前向传播以输入层到隐藏层为例。隐藏层神经元h1的输入加权和为

隐藏层神经元h1的输出：

其中F( x )是激活函数[14]，本文中：

对式（10）求导，有F′( x )=F( x )( 1-F( x ))，这使得用S函数作为激活函数的神经网络比用其他函数的神经网络学习速度快[14]。

反向传播共计分为三个部分。

隐藏层到输出层的反向传播（M2与M3分别为隐藏层和输出层的神经元个数）：

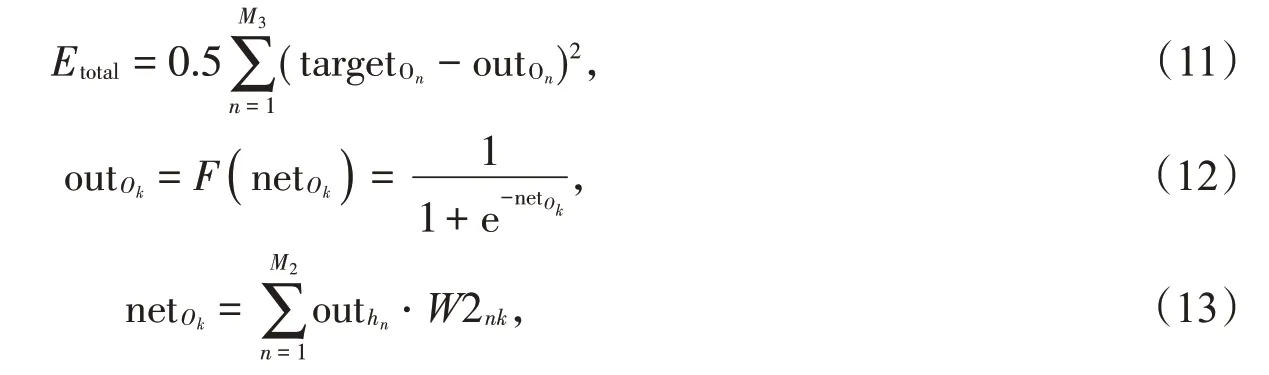
将式（12）和（13）代入式（11）并对W2jk求偏导得：

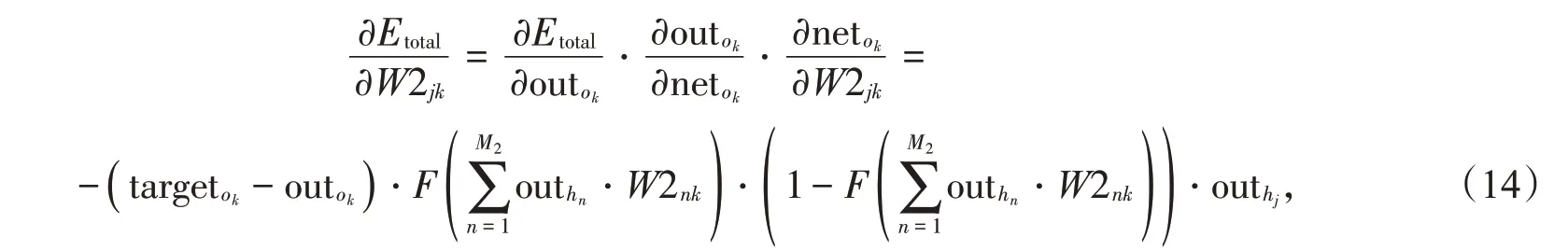
ej是隐藏层节点中重组的向后传播误差：

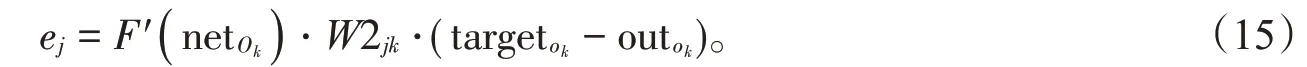
利用对称性，可以轻易得出输入层到隐藏层的反向传播（M1为输入层的神经元个数）：

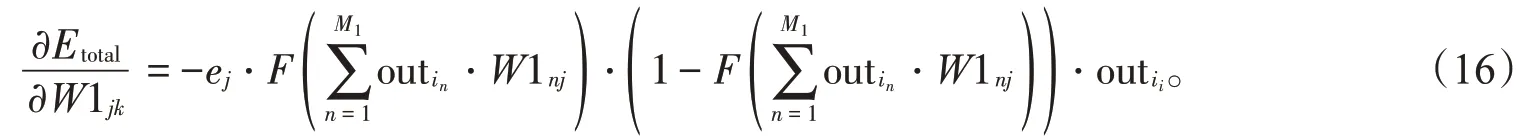
权重更新（LR为学习率）：

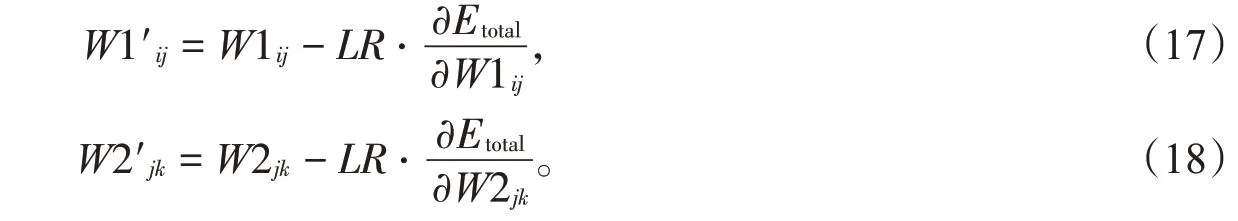
上面的公式没有包含偏置项，是因为偏置项可以通过给每层加入一个恒为1 的输入来消除，因此有偏置可以等价转换成没有偏置的问题，如图3所示。

利用简单的BP 算法，神经网络已经可以训练了，但仍然需要作细微调整。在式（17）和（18）中，有个参数LR，这个参数是无法从数据中学习估计得到，只能靠人的经验进行设计指定，对此需要超参数优化（hyper-parameters optimization，HPO）。在此我们借用这个思想，我们对算法进行优化。人们通常称遍历一次训练集为一个世代（Epoch）。在Epoch=40 时改变学习率LR，虽然只是做了一点微调，但效果是非常棒的，如图6所示。图6中，横坐标为世代数目，纵坐标为均方根误差RMSE：

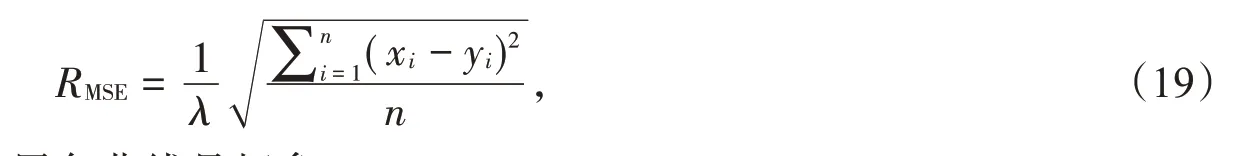
其中xi为预测值，yi为理论值。图6中，黑色曲线是超参数优化的结果，在Epoch=100 时，HPO 得到的RMSE就已经达到我们预期的效果；LR=0.5 在Epoch=400 的时候达到预期效果；至于LR=0.1，甚至达不到预期效果（步长太小，陷入了“不理想的坑”，出不来了）。

注：若将优化的过程看作寻找最低点，那么过程是坑坑洼洼的。开始步长大，可能跳出最优谷。最后步长小，可能跳不出次优谷。

3 结 果

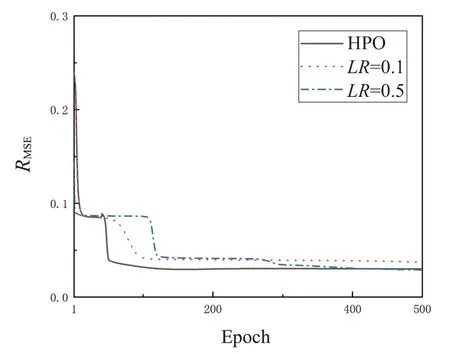
图6 均方根误差

经过上面的努力，我们成功地训练了神经网络，将20%的测试集输入神经网络得出结果（式（8）、（9）），并反归一化后，与平面波展开法得到的结果比较。我们计算了相对误差（式（20）），结果如图7 所示，由于本身是三个输入变量，图7 中只以r1为变量，自然会出现一对多的情形。由图7 得知，该神经网络计算的误差是很小的，完全可以作为一种新的方法用于计算频率。

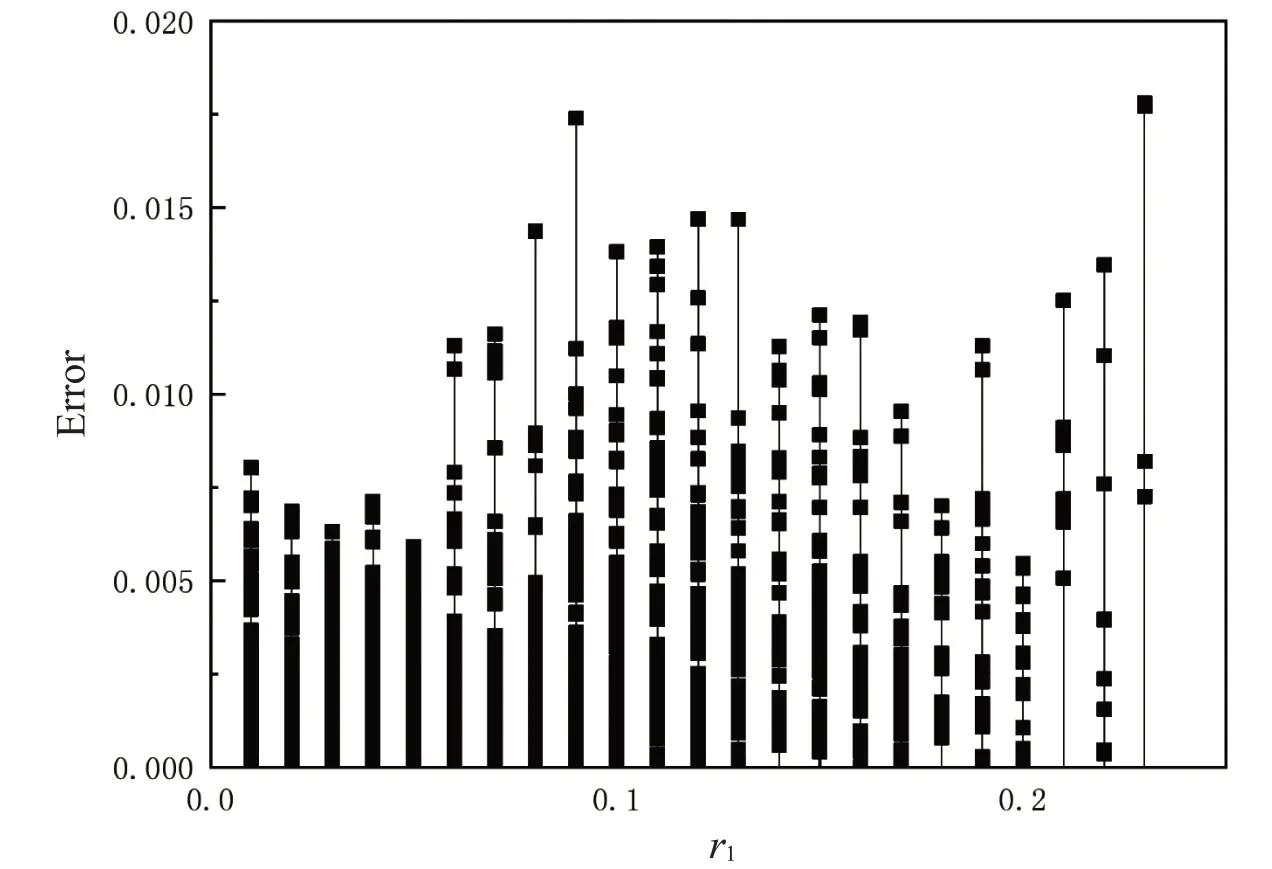
图7 相对误差

到此，我们已经成功计算出K空间的一个点了，再重复进行以上操作就可以画出能带图了。图8(b)展示了应用神经网络与平面波展开法分别计算的能带，结果几乎是一样的。

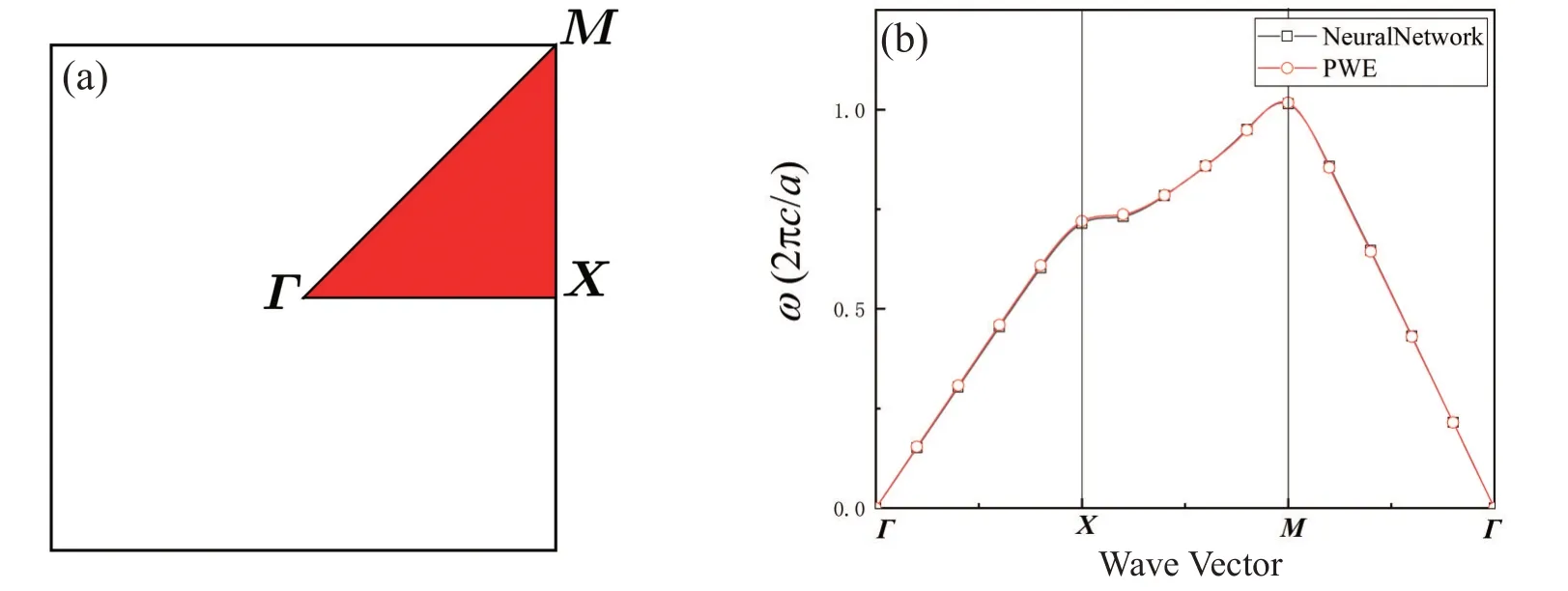
图8 二维正方格子(a)第一布里渊区和(b)TE模第一能带

现在，我们已经成功地利用神经网络来计算光子晶体能带了。在各个程序之间，利用txt文件进行数据交互，特别注意的是，每一列的最小值与最大值是需要单独记录的。

本文通过神经网络来计算光子晶体能带。结果表明，在时间与资源受限的情况下，利用神经网络可以快速得出准确的光子晶体能带。如果将神经网络算法进行优化升级，那么所需数据集将大幅减小，性能会更加优异。