应用灰色Markov模型预测安徽省城镇居民人均可支配收入
滕秀花,戴林送
(安庆师范大学数理学院,安徽安庆246133)
灰色系统[1-2]是由邓聚龙教授在1982年创立的一门新系统科学学科,它以“部分信息已知,部分信息未知的小样本、贫信息”不确定性系统为研究对象。作为灰色系统基础的GM(1,1)模型,主要适用于时间较短、数据资料少、随机性波动不大的问题预测,若对随机性波动较大的数列进行预测,拟合度较差,预测精度不理想。Markov过程[3]是一类具有无记忆性的随机过程。Markov转移概率预测是可以用来揭示系统在不同状态区间转移的内在规律,也就是说,Markov进行数据分析必须要有大量的历史数据,且要求其预测对象一般具有Markov链和平稳过程的特点,这和经济预测问题是大量随时间变化而呈现非平稳随机过程不相符合。安徽省城镇居民人均可支配收入是指安徽省内城镇居民的实际收入中用于安排日常生活的收入,是用来衡量安徽省城镇居民收入水平和生活水平的最重要指标。将城镇居民人均收入看作灰色系统来处理,运用基于GM(1,1)预测模型和Markov预测模型建立的灰色Markov预测[5-8],对安徽省城镇居民人均可支配收入进行预测将会获得更好的结果。
1 灰色Markov预测模型的构建
原始序列设定为X(0)={x (1),x(2),x(3),…,x(n) },满足x(i)≥0,i=1,2,3,…,n,n 为数据量,将安徽省城镇居民人均可支配收入作为原始序列,建立GM(1,1)模型,基本步骤如下。
其中
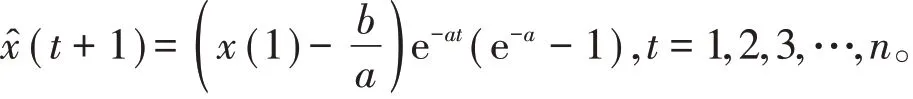
为了下文Markov预测模型的应用,现给出Markov链及相关定义。
定义设{X(n):n ∈ℕ }为随机过程序列,E为状态空间,如果该序列满足以下两个条件:(1)E为至多可列集;(2)对任何正整数m ≥1,0 ≤n1 则称{ X(n):n ∈ℕ }为Markov链,称条件概率p(ijk)(m)=P{ Xm+k=j| Xm=i },i,j ∈E为k步转移概率。 注意到,处理实际问题时,一般考虑一步转移概率,以nij表示由状态Ei经过一步达到状态Ej的频数,从而求出一步转移概率矩阵:,这里s表示状态空间E的状态数。利用当前状态并结合转移矩阵进行预测就是Markov预测。Markov预测在经济、政治等方面有很多应用[4]。 选取安徽省2007—2018年的城镇居民人均可支配收入进行序列分析,数据见表1第2列。 利用Matlab 编程得到GM(1,1)模型的估计参数为aˆ=-0.093 4,bˆ=12 115,从而,得到GM(1,1)模型预测模拟值、预测残差以及相对误差,详细结果可见表1的第3、第4、第5列。 根据表1 中的残差,分为3 个状态,分别为E1、E2、E3,对应的残差范围分别为 各年分支所属状态如表第9列所示。由此可得到一阶转移矩阵为 根据表1 的预测状态,取预测状态所属残差范围的中值,再结合GM(1,1)模型预测值,即为灰色Markov预测模型的预测值,见表1第6列。 表1 安徽省城镇居民人均可支配收入拟合值、预测值比较 根据以上结果,从预测精度对模型进行对比分析,GM(1,1)模型和灰色Markov模型的绝对残差均值分别为608.63 元和301.80 元,市场相对误差分别为3.159%和1.437%,可以看出,灰色Markov 模型会使绝对残差均值和平均相对误差都减少为原来的一半以上。 根据一阶转移矩阵以及2018年的状态为E1,可预测出2019年和2020年的灰色Markov模型的数据分别为37 875.24元与41 654.8元。 对比单一GM(1,1)预测模型与灰色Markov预测模型结果可以发现,灰色Markov预测模型预测精度高,有效地降低了数据的随机性。结合GM(1,1)预测模型所需样本数量少以及Markov预测模型能较好处理波动性偏大的优势,能够有效地预测2019年和2020年安徽省城镇居民人均可支配收入预测值。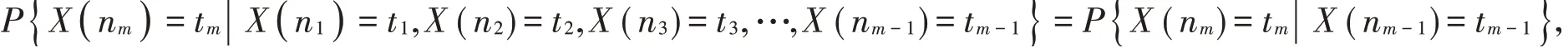
2 灰色Markov预测模型的应用



3 结 论

